Hoe diagnostische plots in r

Lineaire regressiemodellen worden gebruikt om de relatie tussen een of meer voorspellende variabelen en een responsvariabele te beschrijven.

Zodra we echter een regressiemodel hebben geïnstalleerd, is het een goed idee om ook diagnostische plots te maken om de modelresiduen te analyseren en ervoor te zorgen dat een lineair model geschikt is om te gebruiken voor de specifieke gegevens waarmee we werken.

In deze zelfstudie wordt uitgelegd hoe u diagnostische plots voor een bepaald regressiemodel in R maakt en interpreteert.

Voorbeeld: Creëer en interpreteer diagnostische plots in R

Stel dat we een eenvoudig lineair regressiemodel toepassen met behulp van ‚gestudeerde uren‘ om het ‚examencijfer‘ van leerlingen in een bepaalde klas te voorspellen:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

We kunnen de opdracht plot() gebruiken om vier diagnostische plots voor dit regressiemodel te maken:

 #produce diagnostic plots for regression model
plot(model)

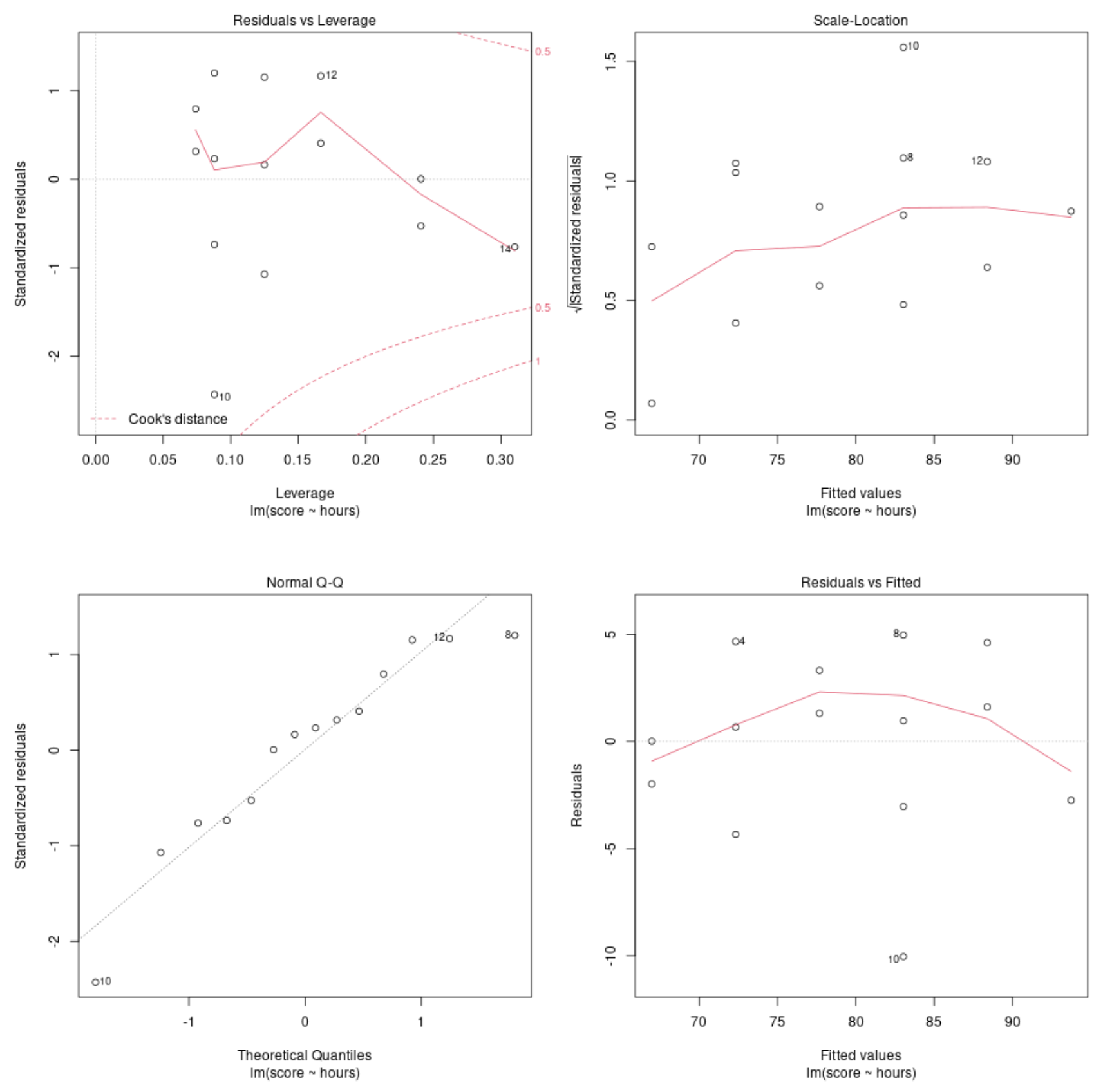
Diagnostische grafiek #1: Residuen vs. Hefboomdiagram

Deze grafiek wordt gebruikt om invloedrijke waarnemingen te identificeren. Als er punten in deze grafiek buiten de afstand van Cook vallen (de stippellijnen), dan is dit een invloedrijke waarneming.

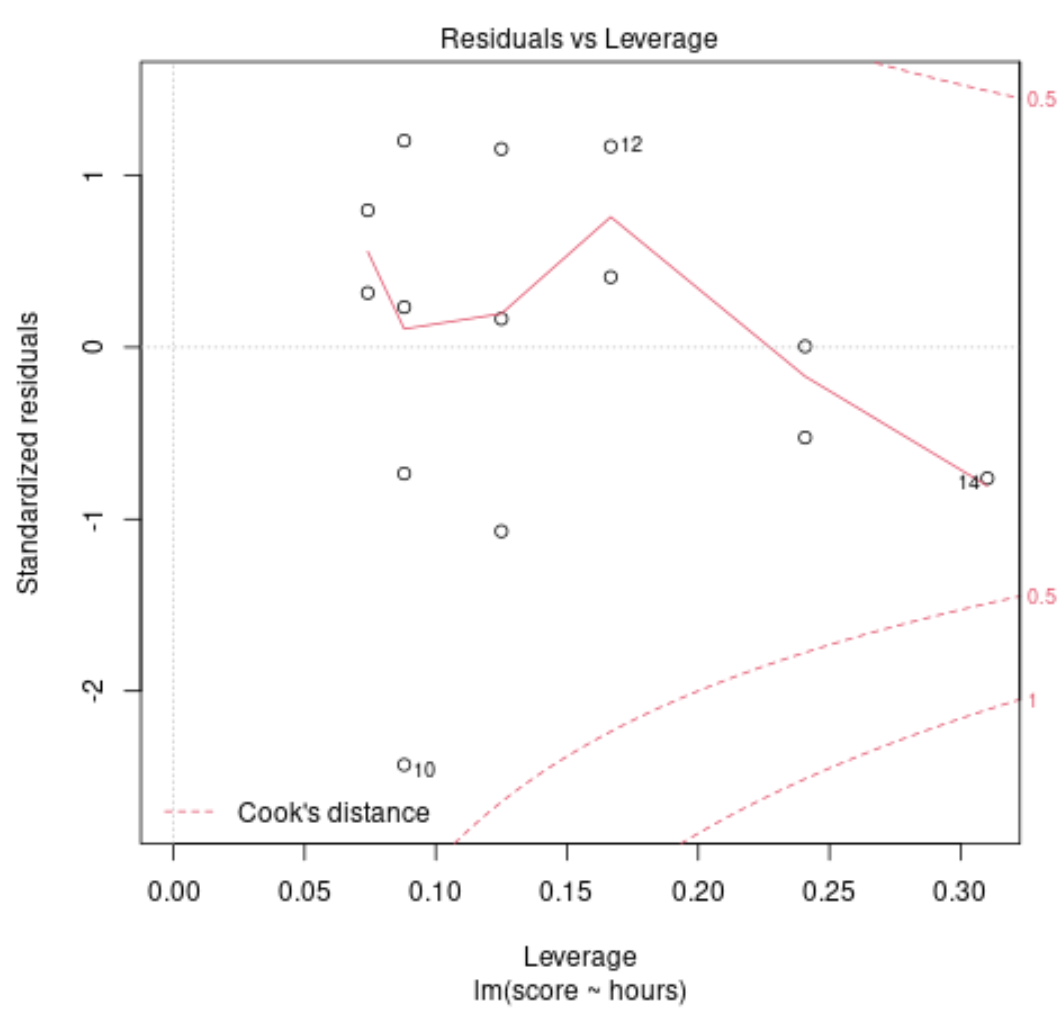
In ons voorbeeld kunnen we zien dat observatie #10 het dichtst bij de Cook-afstandslimiet ligt, maar niet buiten de stippellijn valt. Dit betekent dat er geen overdreven invloedrijke punten in onze dataset zijn.

Diagnostisch plot nr. 2: Schaal- en locatieplot

Deze grafiek wordt gebruikt om de aanname van gelijkheid van variantie (ook wel ‘homoskedasticiteit’ genoemd) onder de residuen van ons regressiemodel te verifiëren. Als de rode lijn ongeveer horizontaal op de grafiek ligt, wordt waarschijnlijk voldaan aan de aanname van gelijke variantie.

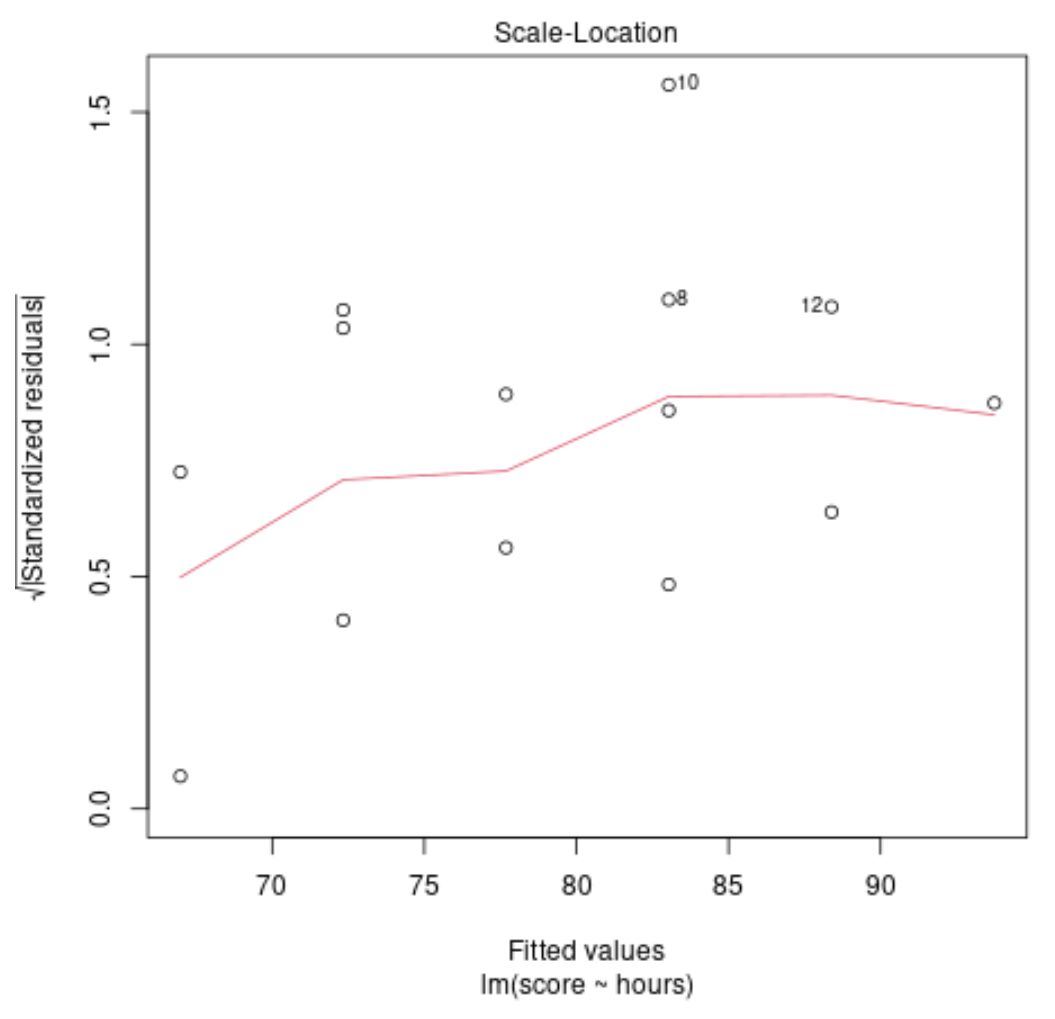
In ons voorbeeld kunnen we zien dat de rode lijn niet precies horizontaal op de plot ligt, maar op geen enkel punt te veel afwijkt. We stellen waarschijnlijk dat de aanname van gelijke variantie in dit geval niet wordt geschonden.

Gerelateerd: Heteroskedasticiteit begrijpen in regressieanalyse

Diagnostische trace #3: normale QQ-trace

Deze plot wordt gebruikt om te bepalen of de residuen uit het regressiemodel normaal verdeeld zijn. Als de punten in deze grafiek ongeveer langs een rechte diagonale lijn liggen, kunnen we aannemen dat de residuen normaal verdeeld zijn.

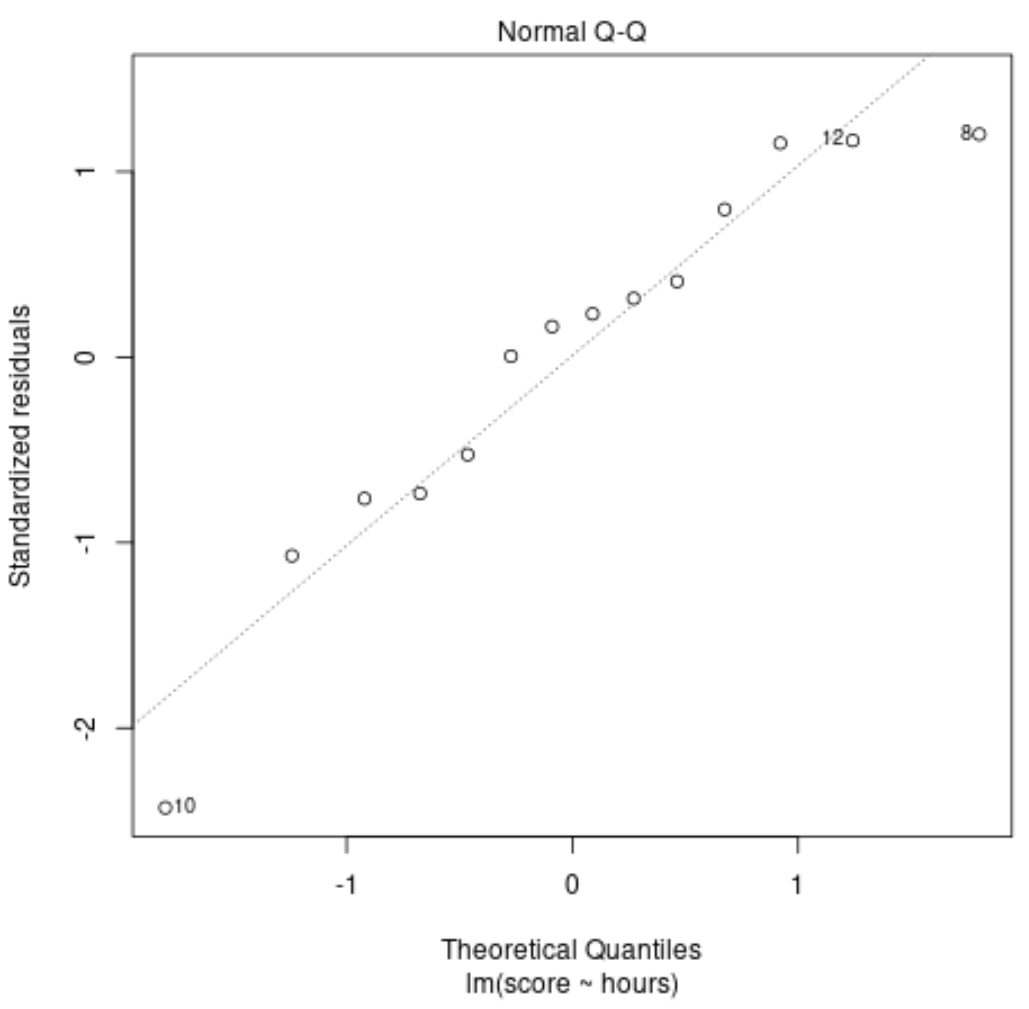
In ons voorbeeld kunnen we zien dat de punten grofweg langs de diagonale rechte lijn liggen. Waarnemingen #10 en #8 wijken een beetje af van de lijn aan de uiteinden, maar niet genoeg om te verklaren dat de residuen niet normaal verdeeld zijn.

Diagnostisch plot #4: Residuen vs. Aangepast plot

Deze plot wordt gebruikt om te bepalen of de residuen niet-lineaire patronen vertonen. Als de rode lijn in het midden van de grafiek ongeveer horizontaal is, kunnen we aannemen dat de residuen een lineair patroon volgen.

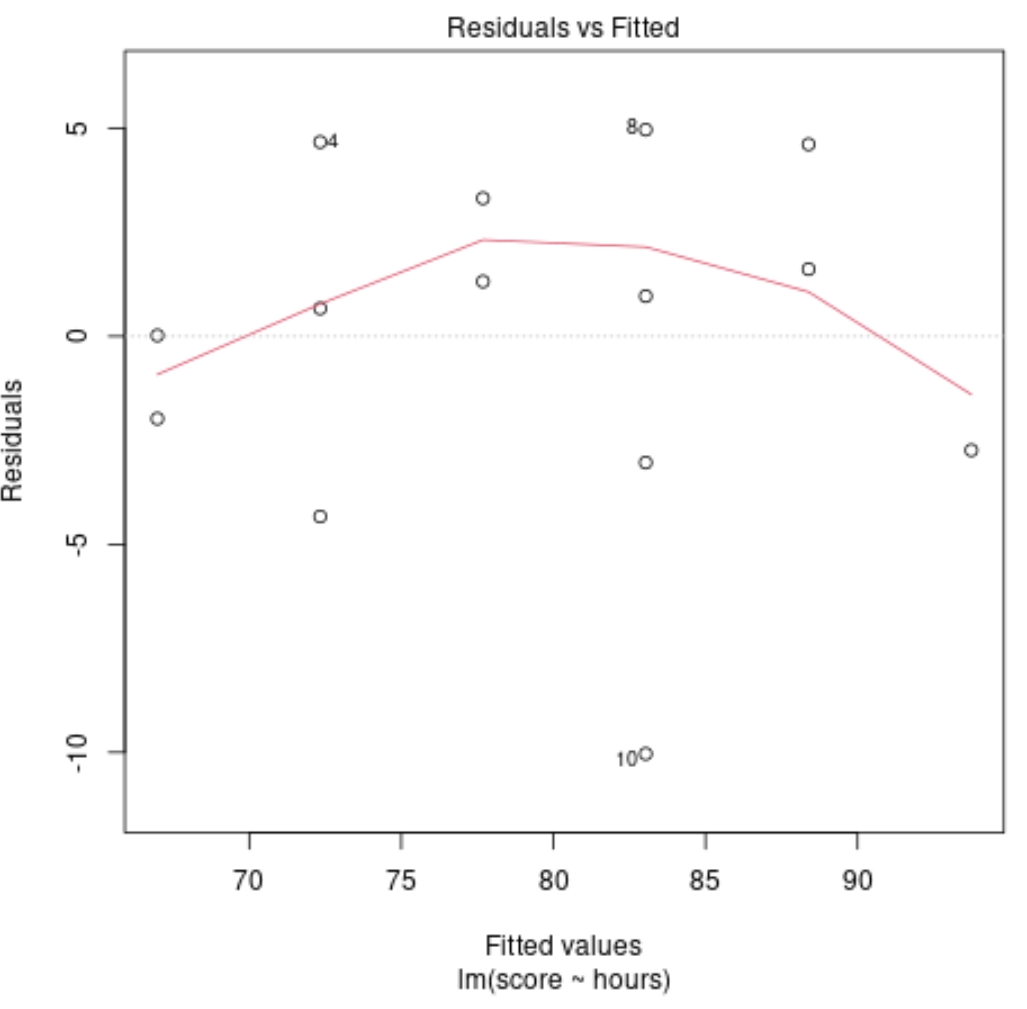
In ons voorbeeld kunnen we zien dat de rode lijn afwijkt van een perfecte horizontale lijn, maar niet significant. We stellen waarschijnlijk dat de residuen een ruwweg lineair patroon volgen en dat een lineair regressiemodel geschikt is voor deze dataset.

Aanvullende bronnen

De vier aannames van lineaire regressie
Wat zijn residuen in de statistiek?
Hoe maak je een restplot in R
Hoe een schaal- en locatieplot te interpreteren