Dichtheidsfunctie

Von Dr.benjamin anderson August 5, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel ontdek je wat de dichtheidsfunctie is, hoe een waarschijnlijkheid wordt berekend op basis van de dichtheidsfunctie en de kenmerken van deze probabilistische functie. Bovendien kunt u zien wat de verschillen zijn tussen de dichtheidsfunctie en de verdelingsfunctie.

Wat is de dichtheidsfunctie?

De dichtheidsfunctie , ook wel de waarschijnlijkheidsdichtheidsfunctie genoemd, is een wiskundige functie die de waarschijnlijkheid beschrijft dat een continue willekeurige variabele een bepaalde waarde aanneemt.

Met andere woorden: de dichtheidsfunctie die bij een variabele hoort, definieert op wiskundige wijze de waarschijnlijkheid dat de variabele een waarde aanneemt.

Laten we bijvoorbeeld zeggen dat de kans dat een volwassen persoon groter is dan 1,80 m in een populatie 35% is, dan zal de dichtheidsfunctie een waarschijnlijkheid van 35% aangeven bij het berekenen van deze waarschijnlijkheid.

Soms wordt de waarschijnlijkheidsdichtheidsfunctie afgekort als PDF.

Bereken een waarschijnlijkheid met de dichtheidsfunctie

Om de waarschijnlijkheid te vinden dat een continue variabele een waarde in een interval aanneemt, is het noodzakelijk om de integraal van de dichtheidsfunctie die bij de genoemde variabele hoort, tussen de grenzen van het interval te berekenen.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Goud

$f(x)$

is de dichtheidsfunctie van de continue willekeurige variabele.

Of met andere woorden: de waarschijnlijkheid dat de variabele een waarde aanneemt in een interval is gelijk aan het gebied onder de dichtheidsfunctie in dat interval.

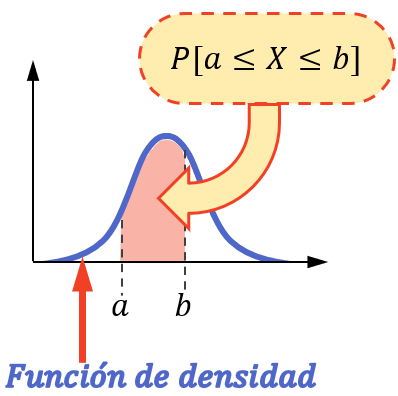
Merk op dat kansberekening alleen op deze manier kan worden uitgevoerd als de statistische variabele een continue verdeling volgt, zoals normale verdeling, exponentiële verdeling, Poisson-verdeling, enz.

Eigenschappen van de dichtheidsfunctie

De dichtheidsfunctie heeft de volgende eigenschappen:

De waarde van de dichtheidsfunctie is nul of positief voor elke waarde van x.

$f(x)\geq 0$

Bovendien is de maximale waarde van de dichtheidsfunctie gelijk aan 1.

$f(x)\leq 1$

In feite is het totale gebied onder de dichtheidsfunctiegrafiek altijd gelijk aan 1, ongeacht de variabele, aangezien het overeenkomt met de verzameling van alle kansen.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Zoals uitgelegd in de vorige sectie, wordt de waarschijnlijkheid dat een continue variabele een waarde aanneemt in een interval berekend met de integraal van de dichtheidsfunctie in dat interval.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Dichtheidsfunctie en distributiefunctie

In dit laatste deel zullen we zien hoe de dichtheidsfunctie en de verdelingsfunctie verschillen, aangezien het twee soorten probabilistische functies zijn die over het algemeen met elkaar verward worden.

Wiskundig gezien is de verdelingsfunctie equivalent aan de integraal van de dichtheidsfunctie , dus de verdelingsfunctie beschrijft de cumulatieve waarschijnlijkheid van een continue variabele.

Dat wil zeggen dat het beeld van de verdelingsfunctie voor elke waarde gelijk is aan de waarschijnlijkheid dat de variabele die waarde of een lagere waarde aanneemt.

De wiskundige relatie tussen deze twee soorten functies is daarom als volgt:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Goud

$f(x)$

is de dichtheidsfunctie en

$F(x)$

is de distributiefunctie.

Merk op hoe de grafische weergave van de dichtheidsfunctie verandert ten opzichte van de verdelingsfunctie van een variabele die een normale verdeling volgt met een gemiddelde van 1 en een standaardafwijking van 0,5:

verschil tussen distributiefunctie en dichtheidsfunctie

Klik op de onderstaande link voor meer informatie over de distributiefunctie:

➤ Zie: distributiefunctie

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder