Wat is erlang-distributie?
De Erlang-verdeling is een waarschijnlijkheidsverdeling die oorspronkelijk door AK Erlang is gemaakt om het aantal telefoongesprekken te modelleren dat een telefoniste van een schakelstation tegelijkertijd kan ontvangen.
Distributie wordt gebruikt in de techniek van telefoonverkeer, wachtrijsystemen, wiskundige biologie en andere gebieden om een verscheidenheid aan fenomenen uit de echte wereld te modelleren.
Eigenschappen van de Erlang-verdeling
De Erlang-verdeling heeft de volgende kansdichtheidsfunctie:
f(x; k, μ) = x k-1 e -x/μ / μk (k-1)!
Goud:
- k: De vormparameter. Het moet een positief geheel getal zijn.
- μ: De schaalparameter. Het moet een positief reëel getal zijn.
Het blijkt dat de Erlang-verdeling een speciaal geval is van de Gamma-verdeling wanneer de vormparameter k beperkt is tot alleen positieve reële gehele getallen.
Merk op dat de schaalparameter het omgekeerde is van de snelheidsparameter, λ, dwz μ = 1/λ.
De Erlang-verdeling heeft de volgende eigenschappen:
- Gemiddeld: k/λ
- Modus: (k-1)/λ
- Verschil: k/λ 2
- Asymmetrie: 2/√k
- Afvlakking: 6/k
De Erlang-distributie heeft de volgende relaties met andere distributies:
- Wanneer de vormparameter k gelijk is aan 1, is de Erlang-verdeling gelijk aan de exponentiële verdeling .
- Wanneer de schaalparameter μ gelijk is aan 2, is de Erlang-verdeling gelijk aan een Chi-kwadraatverdeling met 2 vrijheidsgraden.
Bekijk de Erlang-distributie
De volgende grafiek toont de vorm van de Erlang-verdeling wanneer er verschillende parameters nodig zijn:
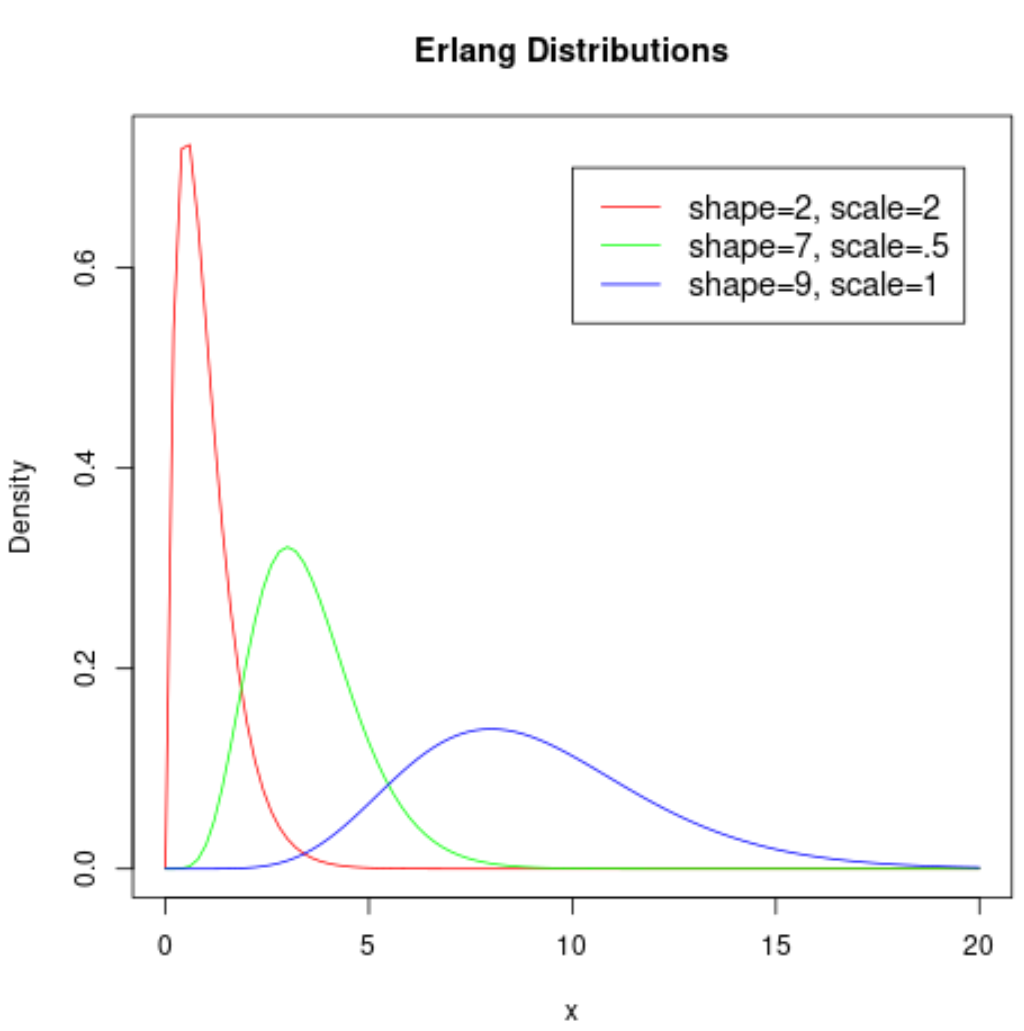
Het is interessant om te zien hoeveel de vorm van de verdeling verandert afhankelijk van de waarden die worden gebruikt voor de vorm- en schaalparameters.
Opmerking: u kunt de R-code die wordt gebruikt om de plot van Erlang-distributies te genereren hier vinden.
Gebruiksgeval
De Erlang-distributie wordt gebruikt in verschillende real-world contexten, waaronder:
1. Callcenters
De Erlang-distributie wordt gebruikt om de tijd tussen inkomende oproepen in een callcenter te modelleren, evenals het verwachte aantal oproepen.
Hierdoor kunnen callcenters weten wat hun personeelscapaciteit op verschillende tijdstippen van de dag moet zijn, zodat ze inkomende oproepen tijdig kunnen afhandelen zonder geld te verliezen door te veel werknemers in dienst te nemen tijdens een dienst. gegeven werk.
2. Medische parameters
De Erlang-verdeling wordt veel gebruikt om de verdeling van de celcyclusduur te modelleren, wat veel verschillende toepassingen heeft in medische omgevingen.
3. Winkelinstellingen
De Erlang-distributie wordt door detailhandelaren gebruikt om de frequentie van vertragingen bij consumentenaankopen te modelleren.
Hierdoor krijgen retailers en andere bedrijven een idee van hoe vaak een bepaalde consument naar verwachting een product of dienst bij hen zal afnemen. Dit helpt bedrijven de voorraad te controleren en personeel te werven.
Aanvullende bronnen
Een inleiding tot de normale verdeling
Een inleiding tot de binominale verdeling
Een inleiding tot de Poisson-verdeling
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder