Een inleiding tot de poisson-verdeling

De Poisson-verdeling is een van de meest populaire verdelingen in de statistiek.

Om de Poisson-verdeling te begrijpen, is het nuttig om eerst de Poisson-experimenten te begrijpen.

Visexperimenten

Een Poisson-experiment is een experiment met de volgende eigenschappen:

• Het aantal successen van het experiment kan worden geteld.
• Het gemiddelde aantal successen dat plaatsvond gedurende een specifiek tijds- (of ruimte-)interval is bekend.
• Elk resultaat is onafhankelijk.
• De kans op een succesvol voorval is evenredig met de grootte van het interval.

Een voorbeeld van een Poisson-experiment is het aantal geboorten per uur in een bepaald ziekenhuis. Stel bijvoorbeeld dat in een bepaald ziekenhuis gemiddeld tien geboorten per uur plaatsvinden. Dit is een Poisson-experiment omdat het de volgende vier eigenschappen heeft:

• Het aantal successen van het experiment kan worden geteld – We kunnen het aantal geboorten tellen.
• Het gemiddelde aantal geboorten dat plaatsvindt gedurende een bepaald tijdsinterval is bekend. Het is bekend dat er gemiddeld 10 geboorten per uur plaatsvinden.
• Elke uitkomst is onafhankelijk – De kans dat een moeder binnen een bepaald uur zal bevallen, is onafhankelijk van de kans dat een andere moeder zal bevallen.
• De kans op succes is evenredig met de grootte van het interval: hoe langer het tijdsinterval, hoe groter de kans op een geboorte.

We kunnen de Poisson-verdeling gebruiken om vragen over waarschijnlijkheden over dit Poisson-experiment te beantwoorden, zoals:

• Wat is de kans dat er in een bepaald uur meer dan twaalf geboorten plaatsvinden?
• Wat is de kans dat er in een bepaald uur minder dan vijf geboorten plaatsvinden?
• Wat is de kans dat er in een bepaald uur tussen de 8 en 11 geboorten zullen plaatsvinden?

De Visverdeling

De Poisson-verdeling beschrijft de waarschijnlijkheid van het behalen van k successen gedurende een bepaald tijdsinterval.

Als een willekeurige variabele X een Poisson-verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = λ ^k * e ^{– λ} / k!

Goud:

• λ: gemiddeld aantal successen dat optreedt tijdens een specifiek interval
• k: aantal successen
• e: een constante gelijk aan ongeveer 2,71828

Stel bijvoorbeeld dat in een bepaald ziekenhuis gemiddeld twee geboorten per uur plaatsvinden. We kunnen de bovenstaande formule gebruiken om de waarschijnlijkheid van 0, 1, 2, 3 geboorten, enz. te bepalen. in een bepaald uur:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

We kunnen de waarschijnlijkheid van een willekeurig aantal geboorten tot in het oneindige berekenen. Vervolgens maken we een eenvoudig histogram om deze waarschijnlijkheidsverdeling te visualiseren:

Berekening van cumulatieve Poisson-kansen

Het is eenvoudig om een enkele Poisson-waarschijnlijkheid te berekenen (bijvoorbeeld de kans dat een ziekenhuis drie geboorten in een bepaald uur meemaakt) met behulp van de bovenstaande formule, maar om cumulatieve Poisson-waarschijnlijkheden te berekenen moeten we individuele kansen optellen.

Laten we bijvoorbeeld zeggen dat we de waarschijnlijkheid willen weten dat het ziekenhuis binnen een bepaald uur één of minder geboorten zal meemaken. Om deze waarschijnlijkheid te berekenen, gebruiken we de volgende formule:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

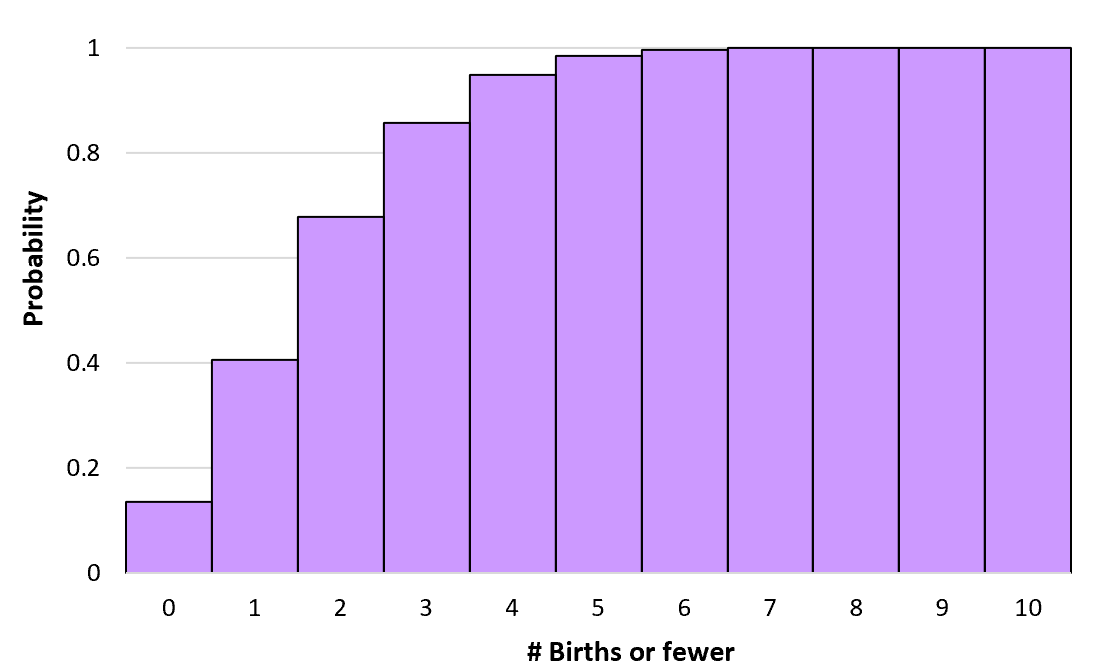
Dit wordt een cumulatieve waarschijnlijkheid genoemd, omdat het gaat om het optellen van meerdere kansen. We kunnen de cumulatieve waarschijnlijkheid berekenen van k of minder geboorten in een bepaald uur met behulp van een soortgelijke formule:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

We kunnen deze cumulatieve kansen berekenen voor elk aantal geboorten tot in het oneindige. We kunnen vervolgens een histogram maken om deze cumulatieve waarschijnlijkheidsverdeling te visualiseren:

Eigenschappen van de Poisson-verdeling

De Poissonverdeling heeft de volgende eigenschappen:

Het gemiddelde van de verdeling is λ .

De variantie van de verdeling is ook λ .

De standaardafwijking van de verdeling is √ λ .

Stel bijvoorbeeld dat een ziekenhuis gemiddeld twee geboorten per uur heeft.

Het gemiddelde aantal verwachte geboorten in een bepaald uur is λ = 2 geboorten.

De variantie in het aantal geboorten dat we verwachten is λ = 2 geboorten.

Praktijkproblemen bij de visdistributie

Gebruik de volgende oefenproblemen om uw kennis van de Poisson-verdeling te testen.

Opmerking: we zullen de Poisson-verdelingscalculator gebruiken om de antwoorden op deze vragen te berekenen.

Probleem 1

Vraag: We weten dat een bepaalde website 10 verkopen per uur genereert. Wat is de kans dat de site binnen een bepaald uur precies 8 verkopen genereert?

Antwoord: Met behulp van de Poisson-verdelingscalculator met λ = 10 en x = 8 vinden we dat P(X=8) = 0,1126 .

Probleem 2

Vraag: We weten dat een bepaalde makelaar gemiddeld 5 verkopen per maand maakt. Wat is de kans dat ze in een bepaalde maand meer dan zeven verkopen zal realiseren?

Antwoord: Met behulp van de Poisson-verdelingscalculator met λ = 5 en x = 7 vinden we dat P(X>7) = 0,13337 .

Probleem 3

Vraag: We weten dat een bepaald ziekenhuis 4 bevallingen per uur ervaart. Wat is de kans dat er in een bepaald uur vier of minder geboorten zullen plaatsvinden?

Antwoord: Met behulp van de Poisson-verdelingscalculator met λ = 4 en x = 4 vinden we dat P(X≤4) = 0,62884 .

Aanvullende bronnen

In de volgende artikelen wordt uitgelegd hoe u de Poisson-verdeling in verschillende statistische software kunt gebruiken:

Hoe de Poisson-verdeling in R te gebruiken
Hoe Poisson-distributie in Excel te gebruiken
Hoe Poisson-kansen te berekenen op een TI-84-rekenmachine
Voorbeelden uit de echte wereld van de Poisson-verdeling
Visdistributiecalculator