Een inleiding tot de driehoeksverdeling

De driehoekige verdeling is een continue kansverdeling met een driehoekige kansdichtheidsfunctie.

Het wordt gedefinieerd door drie waarden:

• De minimumwaarde heeft
• De maximale waarde b
• De maximale waarde c

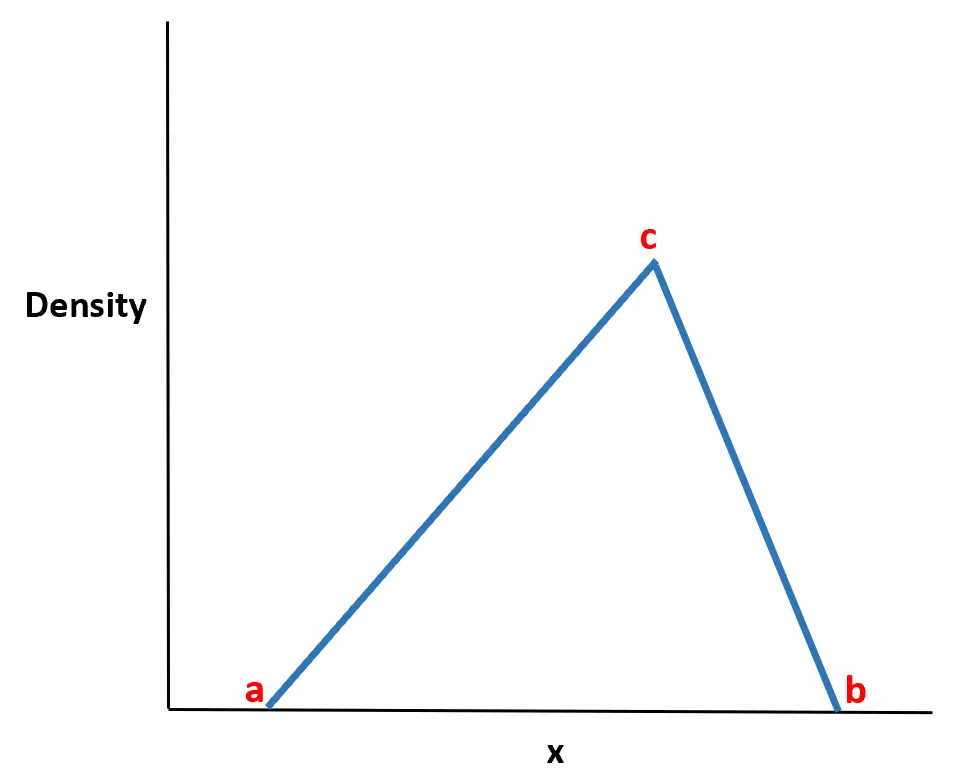
De naam van de verdeling komt van het feit dat de kansdichtheidsfunctie de vorm heeft van een driehoek.

Het blijkt dat deze verdeling buitengewoon nuttig is in de echte wereld, omdat we vaak de minimale waarde (a), de maximale waarde (b) en de meest waarschijnlijke waarde (c) kunnen schatten die een willekeurige variabele zal aannemen. kan vaak het gedrag van willekeurige variabelen modelleren met behulp van een driehoekige verdeling en alleen deze drie waarden kent.

Een restaurant kan bijvoorbeeld schatten dat de totale omzet voor de komende week minimaal €10.000, maximaal €30.000 en hoogstwaarschijnlijk €25.000 zal bedragen.

Door alleen deze drie getallen te gebruiken, konden ze een driehoekige verdeling gebruiken om de waarschijnlijkheid van een bepaald aantal verkopen te bepalen.

Eigenschappen van de driehoekige verdeling

De driehoekige verdeling heeft de volgende eigenschappen:

Pdf:

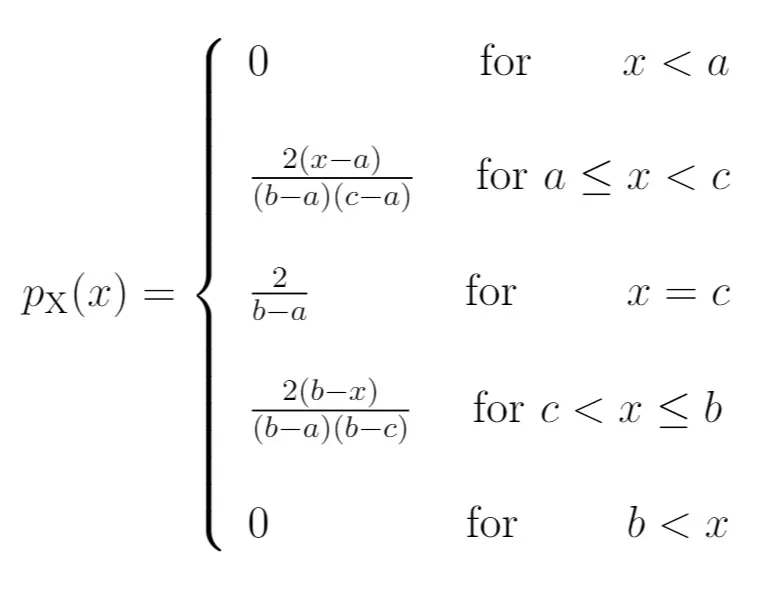
CDF:

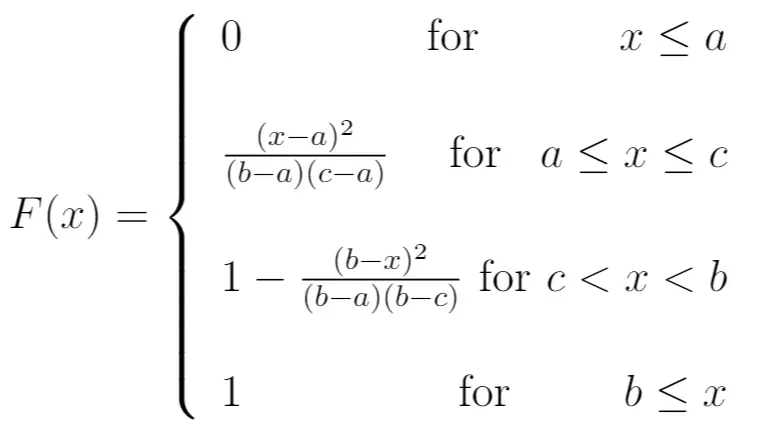
Gemiddeld: (a + b + c) / 3

Modus: c

Variantie: (a ² + b ² + c ² – ab – ac – bc) / 18

Voorbeeld van het gebruik van de driehoekige verdeling

Laten we teruggaan naar het vorige voorbeeld. Laten we zeggen dat een restaurant schat dat de totale omzet voor de komende week minimaal $ 10.000, maximaal $ 30.000 en hoogstwaarschijnlijk $ 25.000 zal bedragen.

Wat is de kans dat het restaurant een totale omzet van minder dan $ 20.000 heeft?

Om deze vraag te beantwoorden, kunnen we x = totale omzet vragen. We weten dat x tussen de minimumwaarde a van $10.000 en de maximumwaarde c van $25.000 ligt.

Volgens de pdf kunnen we dus de volgende vergelijking gebruiken om de waarschijnlijkheid te bepalen dat het restaurant een totale omzet van minder dan $ 20.000 heeft:

• P(X < $20.000) = (xa) ² / ((ba)(ca))
• P(X < $20.000) = (20.000-10.000) ² / ((30.000-10.000)(25.000-10.000))
• P(X <$20.000) = 0,333

De kans dat het restaurant een totale omzet van minder dan $ 20.000 heeft, is 0,333 .

Wat is de gemiddelde verwachte omzet voor het restaurant?

We kunnen de verwachte gemiddelde omzet berekenen met behulp van de eerder gegeven formule voor het gemiddelde:

• Gemiddeld = (a + b + c) / 3
• Gemiddeld = ($10.000 + $30.000 + $25.000) / 3
• Gemiddeld = $ 21.667

De gemiddelde verwachte omzet bedraagt 21.667 .

Aanvullende bronnen

De volgende tutorials bieden introducties tot andere veelgebruikte distributies:

De normale verdeling
De binominale verdeling
De Visverdeling
De geometrische verdeling