Drieweg-anova: definitie en voorbeeld

Een drieweg-ANOVA wordt gebruikt om te bepalen hoe drie verschillende factoren een responsvariabele beïnvloeden.

Drieweg-ANOVA’s komen minder vaak voor dan een eenrichtings-ANOVA (met slechts één factor) of een tweeweg-ANOVA (met slechts twee factoren), maar ze worden nog steeds op verschillende gebieden gebruikt.

Telkens wanneer we een drieweg-ANOVA uitvoeren, willen we weten of er een statistisch significante relatie bestaat tussen elke factor en de responsvariabele, en of er interactie-effecten tussen de factoren zijn.

Deze tutorial toont verschillende scenario’s waarin u een drieweg-ANOVA kunt gebruiken, evenals een voorbeeld van hoe u er een kunt uitvoeren.

Wanneer moet u een drieweg-ANOVA gebruiken?

Hier volgen enkele scenario’s waarin u een drieweg-ANOVA kunt gebruiken:

Scenario 1: Botanie

Een botanicus wil misschien bepalen hoe (1) blootstelling aan de zon, (2) de waterfrequentie en (3) het soort kunstmest de plantengroei beïnvloeden.

In dit scenario zou ze een drieweg-ANOVA kunnen uitvoeren, omdat er drie factoren en één responsvariabele zijn.

Scenario 2: Detailhandel

Een manager van een winkel wil mogelijk bepalen hoe (1) dag van de week, (2) winkellocatie en (3) advertentiecampagnes de totale omzet beïnvloeden.

In dit scenario zou hij een drieweg-ANOVA kunnen uitvoeren, aangezien er drie factoren en één responsvariabele zijn.

Scenario 3: Medisch

Een arts wil misschien bepalen hoe (1) geslacht, (2) dieet en (3) bewegingsgewoonten het gewicht beïnvloeden.

In dit scenario zou ze een drieweg-ANOVA kunnen uitvoeren, omdat er drie factoren en één responsvariabele zijn.

Drieweg-ANOVA: voorbeeld

Stel dat een onderzoeker wil bepalen of trainingsprogramma, geslacht en sportverdeling de spronghoogte beïnvloeden.

Om dit te testen, kan hij een drieweg-ANOVA uitvoeren met de volgende factoren:

• 1. Trainingsprogramma (programma 1 versus programma 2)
• 2. Geslacht (man of vrouw)
• 3. Sportdivisie (divisie I versus divisie II)

De enige responsvariabele is de spronghoogte .

Stel dat hij deze gegevens over 40 mensen verzamelt:

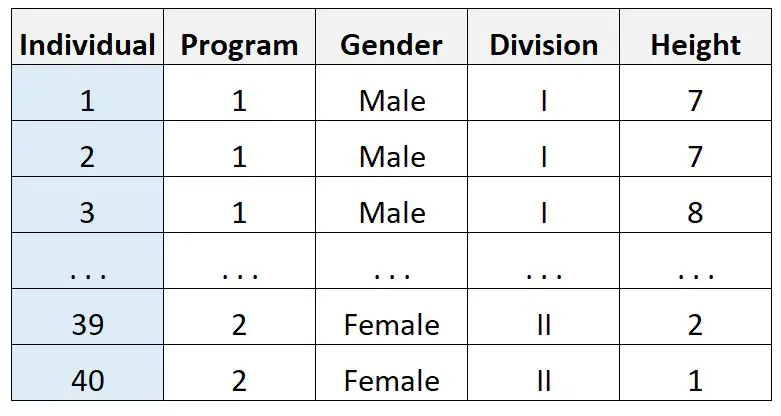
Vervolgens gebruikt hij statistische software om een drieweg-ANOVA uit te voeren en krijgt het volgende resultaat:

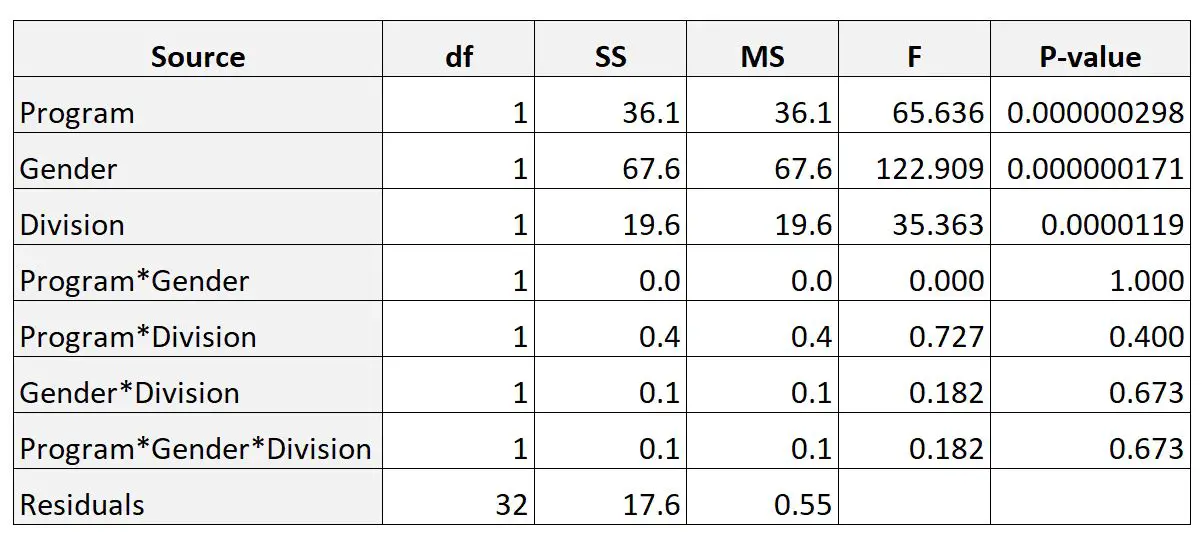
In de kolom P-waarde wordt de P-waarde voor elke individuele factor weergegeven, evenals de interacties tussen de factoren.

Uit de resultaten kunnen we opmaken dat geen van de interacties tussen de drie factoren statistisch significant was.

We kunnen ook zien dat elk van de drie factoren (programma, geslacht en verdeeldheid) statistisch significant was.

Concluderend zouden we kunnen zeggen dat trainingsprogramma, geslacht en divisie allemaal belangrijke indicatoren zijn voor de toegenomen spronghoogte bij spelers.

We zouden ook zeggen dat er geen significante interactie-effecten zijn tussen deze drie factoren.

Opmerking : in de praktijk berekenen we ook de gemiddelde spronghoogte voor elk programma, geslacht en divisie, zodat we kunnen bepalen welke niveaus van elke factor verband houden met een toename in spronghoogte.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een drieweg-ANOVA uitvoert in R en Python:

Een drieweg-ANOVA uitvoeren in R
Hoe u een drieweg-ANOVA uitvoert in Python