Hoe de test van dunnett te gebruiken voor meerdere vergelijkingen

Een ANOVA (variantieanalyse) wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Als de p-waarde van de ANOVA onder een bepaald gekozen significantieniveau ligt, kunnen we de nulhypothese verwerpen en concluderen dat we voldoende bewijs hebben om te zeggen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Dit vertelt ons echter niet welke groepen van elkaar verschillen. Dit vertelt ons eenvoudigweg dat niet alle groepsgemiddelden gelijk zijn. Om precies te weten welke groepen van elkaar verschillen, moeten we eenpost-hoc test uitvoeren.

Als een van de groepen in het onderzoek als de controlegroep wordt beschouwd, moeten we de test van Dunnett gebruiken als post-hoc-test na de ANOVA.

Dunnett-test: definitie

We kunnen de volgende twee stappen gebruiken om de Dunnett-test uit te voeren:

Stap 1: Vind de kritische waarde van Dunnett.

Eerst moeten we de kritische waarde van Dunnett vinden. Dit wordt als volgt berekend:

Kritische waarde Dunnett: t _d √ 2MS _w /n

Goud:

• t _d : De waarde gevonden in de tabel van Dunnett voor een bepaald alfaniveau, aantal groepen en groepssteekproefgroottes.
• MS _w : De gemiddelde kwadraten van “binnen groep” in de ANOVA-uitvoertabel
• n: Groepssteekproefomvang

Stap 2: Vergelijk de verschillen tussen groepsgemiddelden met de kritische waarde van Dunnett.

Vervolgens berekenen we het absolute verschil tussen het gemiddelde van elke groep en het gemiddelde van de controlegroep. Als het verschil de kritische waarde van Dunnett overschrijdt, wordt dit verschil statistisch significant genoemd.

Het volgende voorbeeld laat zien hoe u de Dunnett-test in de praktijk kunt uitvoeren.

Dunnett-test: voorbeeld

Stel dat een docent wil weten of twee nieuwe studietechnieken de potentie hebben om de toetsscores van haar leerlingen te verbeteren. Om dit te testen verdeelt ze haar klas van dertig leerlingen willekeurig in de volgende drie groepen:

• Controlegroep: 10 studenten
• Nieuwe technische studie 1: 10 studenten
• Nieuwe technische studie 2: 10 studenten

Na een week gebruik te hebben gemaakt van de toegewezen studietechniek, legt elke student hetzelfde examen af. De resultaten zijn als volgt:

• Gemiddelde examenscore van de controlegroep: 81,6
• Gemiddelde examenscore voor de nieuwe studietechniek groep 1: 85,8
• Gemiddelde score op het groepsexamen Nieuwe Studietechniek 2: 87,7
• Gemiddelde kwadraten van “Binnen Groep” in ANOVA-uitvoertabel: 23.3

Met deze informatie kunnen we de Dunnett-test uitvoeren om te bepalen of een van de twee nieuwe studietechnieken significant andere gemiddelde examenscores oplevert dan de controlegroep.

Stap 1: Vind de kritische waarde van Dunnett.

Gebruikmakend van α = 0,05, groepssteekproefgrootte n = 10 en groepstotaal = 3, vertelt de tabel van Dunnett ons dat we een waarde van 2,57 moeten gebruiken bij het berekenen van de kritische waarde.

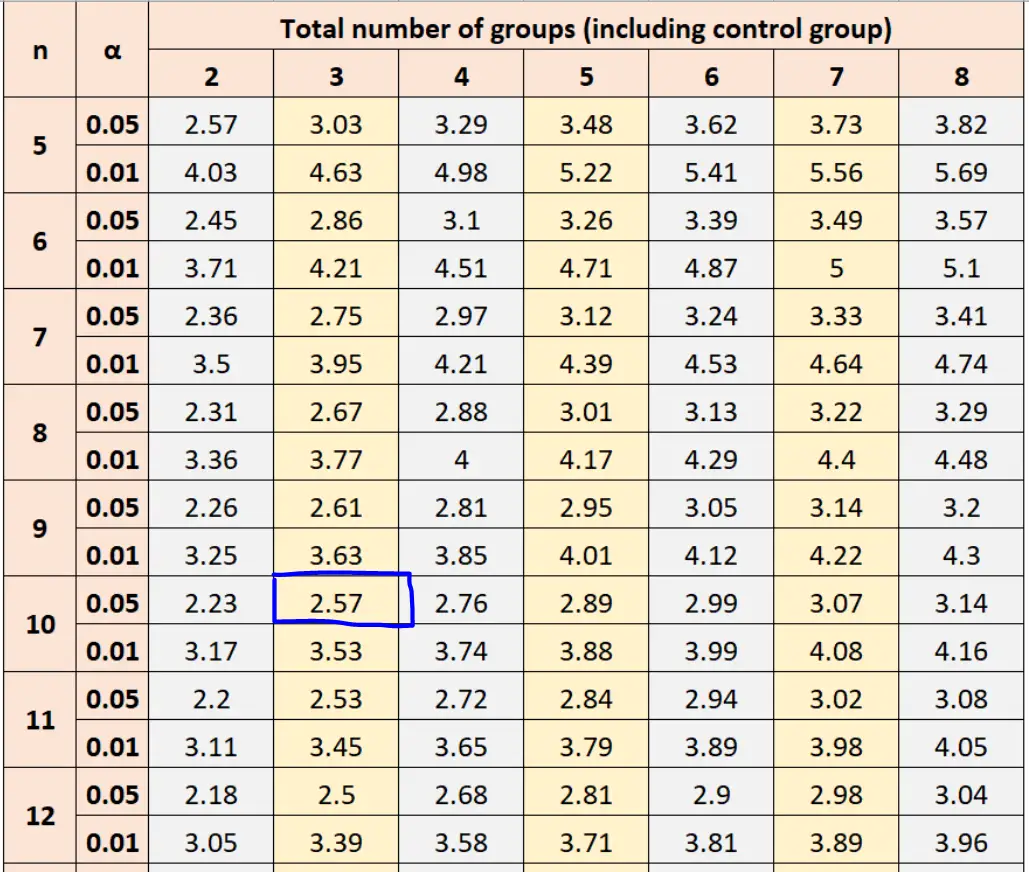
Vervolgens kunnen we dit getal in de formule stoppen om de kritische Dunnett-waarde te vinden:

Kritische waarde van Dunnett: t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548

Stap 2: Vergelijk de verschillen tussen groepsgemiddelden met de kritische waarde van Dunnett.

De absolute verschillen tussen de gemiddelden van elke onderzoekstechniek en die van de controlegroep zijn als volgt:

• Buikspieren. verschil tussen de nieuwe techniek 1 en de besturing: |85.8 – 81.6| = 4,2
• Buikspieren. verschil tussen de nieuwe techniek 2 en de besturing: |87.7 – 81.6| = 6,1

Alleen het absolute verschil tussen techniek 2 en de controlegroep is groter dan de Dunnett kritische waarde van 5.548 .

We kunnen dus zeggen dat nieuwe studietechniek #2 significant andere examenresultaten oplevert dan de controlegroep, maar dit is niet het geval voor nieuwe studietechniek #1.

Aanvullende bronnen

Een inleiding tot One-Way ANOVA
Een handleiding voor het gebruik van post-hoctesten met ANOVA
Hoe de Dunnett-test uit te voeren in R