Hoe de dunnett-test uit te voeren in r

Eenpost-hoctest is een soort test die wordt uitgevoerd na een ANOVA om te bepalen welke groepsgemiddelden statistisch significant van elkaar verschillen.

Als een van de studiegroepen als de controlegroep wordt beschouwd, moeten we de test van Dunnett als post-hoctest gebruiken.

In deze tutorial wordt uitgelegd hoe u de Dunnett-test uitvoert in R.

Voorbeeld: Dunnett-test in R

Stel dat een docent wil weten of twee nieuwe studietechnieken de potentie hebben om de toetsscores van haar leerlingen te verbeteren. Om dit te testen verdeelt ze haar klas van dertig leerlingen willekeurig in de volgende drie groepen:

• Controlegroep: 10 studenten
• Nieuwe technische studie 1: 10 studenten
• Nieuwe technische studie 2: 10 studenten

Na een week gebruik te hebben gemaakt van de toegewezen studietechniek, legt elke student hetzelfde examen af.

We kunnen de volgende stappen in R gebruiken om een dataset te creëren, de groepsgemiddelden te visualiseren, een eenrichtings-ANOVA uit te voeren en tenslotte de test van Dunnett uit te voeren om te bepalen welke nieuwe onderzoekstechniek (indien aanwezig) andere resultaten oplevert in vergelijking met de controlegroep .

Stap 1: Maak de gegevensset.

De volgende code laat zien hoe u een dataset maakt met de examenresultaten van alle 30 studenten:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Stap 2: Bekijk de examenresultaten voor elke groep.

De volgende code laat zien hoe u boxplots kunt maken om de verdeling van de examenresultaten voor elke groep te visualiseren:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

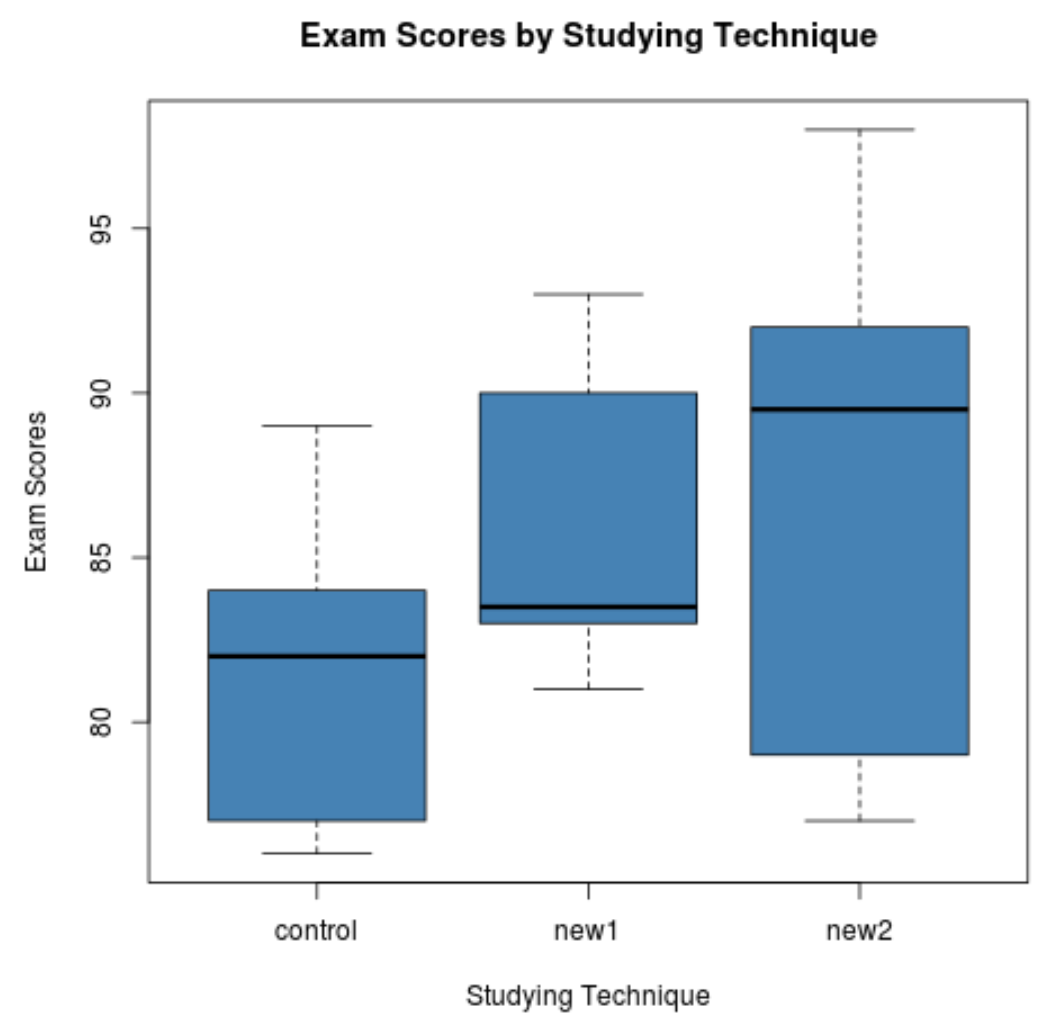
Alleen al aan de boxplots kunnen we zien dat de verdeling van examenscores voor elke studietechniek heel verschillend is. Vervolgens voeren we een eenrichtings-ANOVA uit om te bepalen of deze verschillen statistisch significant zijn.

Gerelateerd: Meerdere boxplots in één diagram plotten in R

Stap 3: Voer een eenrichtings-ANOVA uit.

De volgende code laat zien hoe u een eenrichtings-ANOVA uitvoert om te testen op verschillen tussen de gemiddelde examenscores in elke groep:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Aangezien de totale p-waarde ( 0,0476 ) kleiner is dan 0,05, geeft dit aan dat niet elke groep dezelfde gemiddelde examenscore heeft. Vervolgens voeren we de Dunnett-test uit om te bepalen welke studietechniek gemiddelde examenscores oplevert die afwijken van die van de controlegroep.

Stap 4: Voer de Dunnett-test uit.

Om de Dunnett-test in R uit te voeren, kunnen we de functie DunnettTest() uit de DescTools- bibliotheek gebruiken, die de volgende syntaxis gebruikt:

Dunnett-test(x, g)

Goud:

• x: een numerieke vector van datawaarden (bijvoorbeeld examenresultaten)
• g: Een vector die de namen van groepen specificeert (bijvoorbeeld studietechniek)

De volgende code laat zien hoe u deze functie voor ons voorbeeld kunt gebruiken:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

De manier om het resultaat te interpreteren is als volgt:

• Het gemiddelde verschil in examenscores tussen de nieuwe studietechniek 1 en de controlegroep is 4,2. De overeenkomstige p-waarde is 0,1787 .
• Het gemiddelde verschil in examenscores tussen de nieuwe studietechniek 2 en de controlegroep is 6,4. De overeenkomstige p-waarde is 0,0296 .

Op basis van de resultaten kunnen we zien dat het bestuderen van Techniek 2 de enige techniek is die gemiddelde examenscores oplevert die significant (p = 0,0296) verschillen van die van de controlegroep.

Aanvullende bronnen

Een inleiding tot One-Way ANOVA
Eenrichtings-ANOVA uitvoeren in R
Hoe de Tukey-test uit te voeren in R