Hoe u een one-sample t-test uitvoert in spss

Een one-sample t-test wordt gebruikt om te testen of het gemiddelde van een populatie gelijk is aan een bepaalde waarde.

In deze tutorial wordt uitgelegd hoe u een one-sample t-test uitvoert in SPSS.

Voorbeeld: t-test met één monster in SPSS

Een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. Ze neemt een willekeurig monster van twaalf planten en noteert hun hoogte in centimeters:

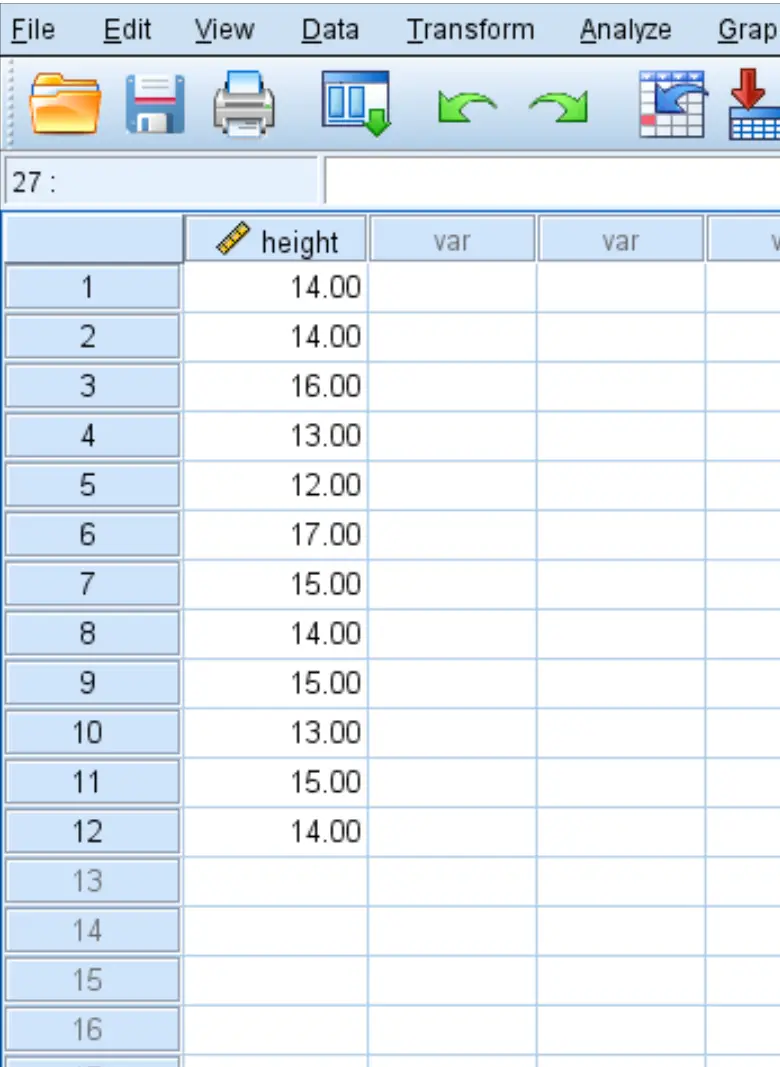
Gebruik de volgende stappen om een t-test met één monster uit te voeren om te bepalen of de werkelijke gemiddelde hoogte van deze plantensoort gelijk is aan 15 inch, op basis van de volgende nul- en alternatieve hypothesen:

• H ₀ : μ = 15 (het werkelijke populatiegemiddelde is gelijk aan 15 inch)
• H ₁ : μ ≠ 15 (het werkelijke populatiegemiddelde is niet gelijk aan 15 inch)

Gebruik een significantieniveau van α = 0,05.

Stap 1: Kies de t-testoptie met één monster.

Klik op het tabblad Analyseren , vervolgens op Middelen vergelijken en vervolgens op T-test met één monster :

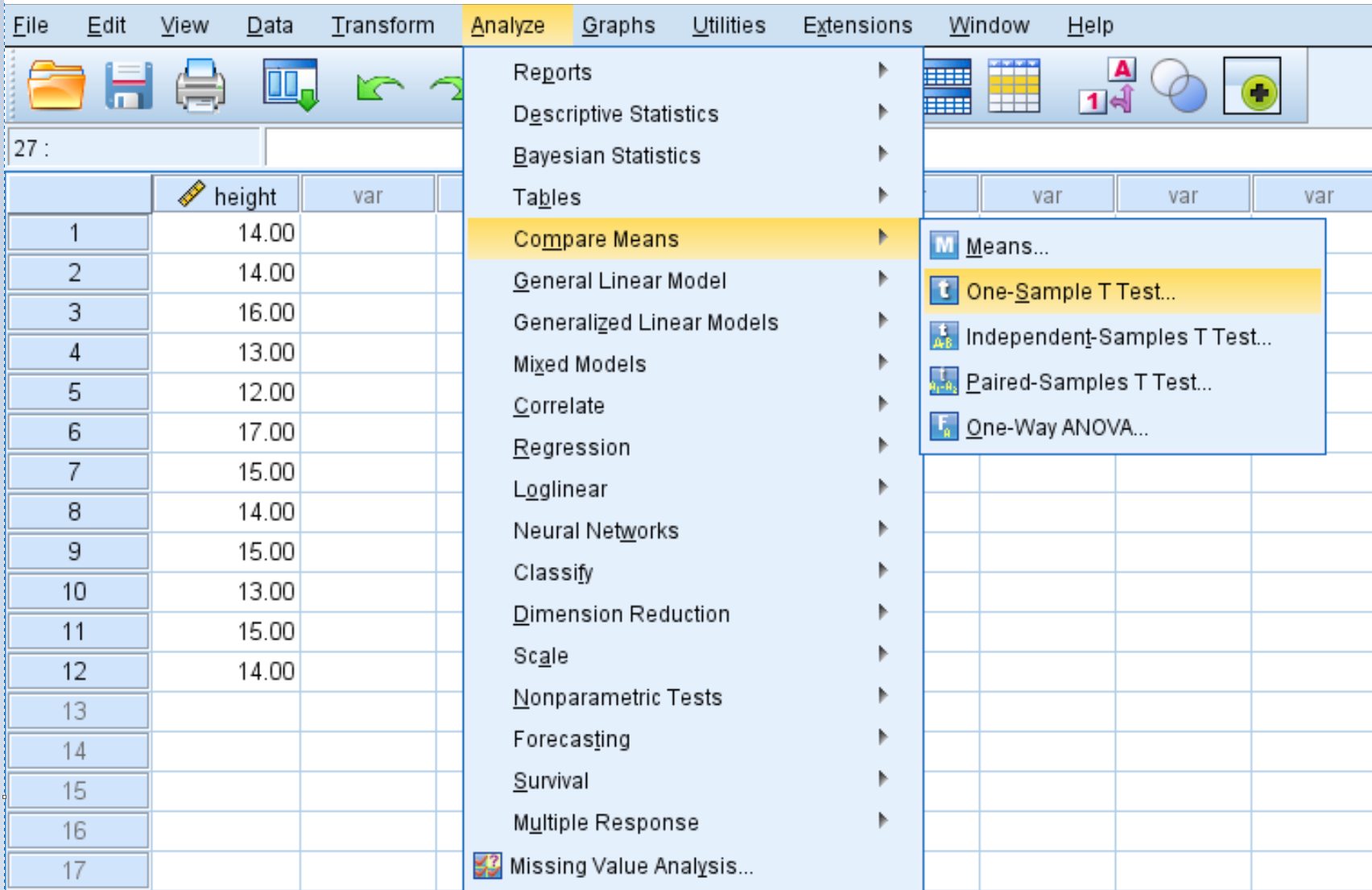
Stap 2: Vul de waarden in die nodig zijn om de one-sample t-test uit te voeren.

Zodra u op One-Sample T Test klikt, verschijnt het volgende venster:

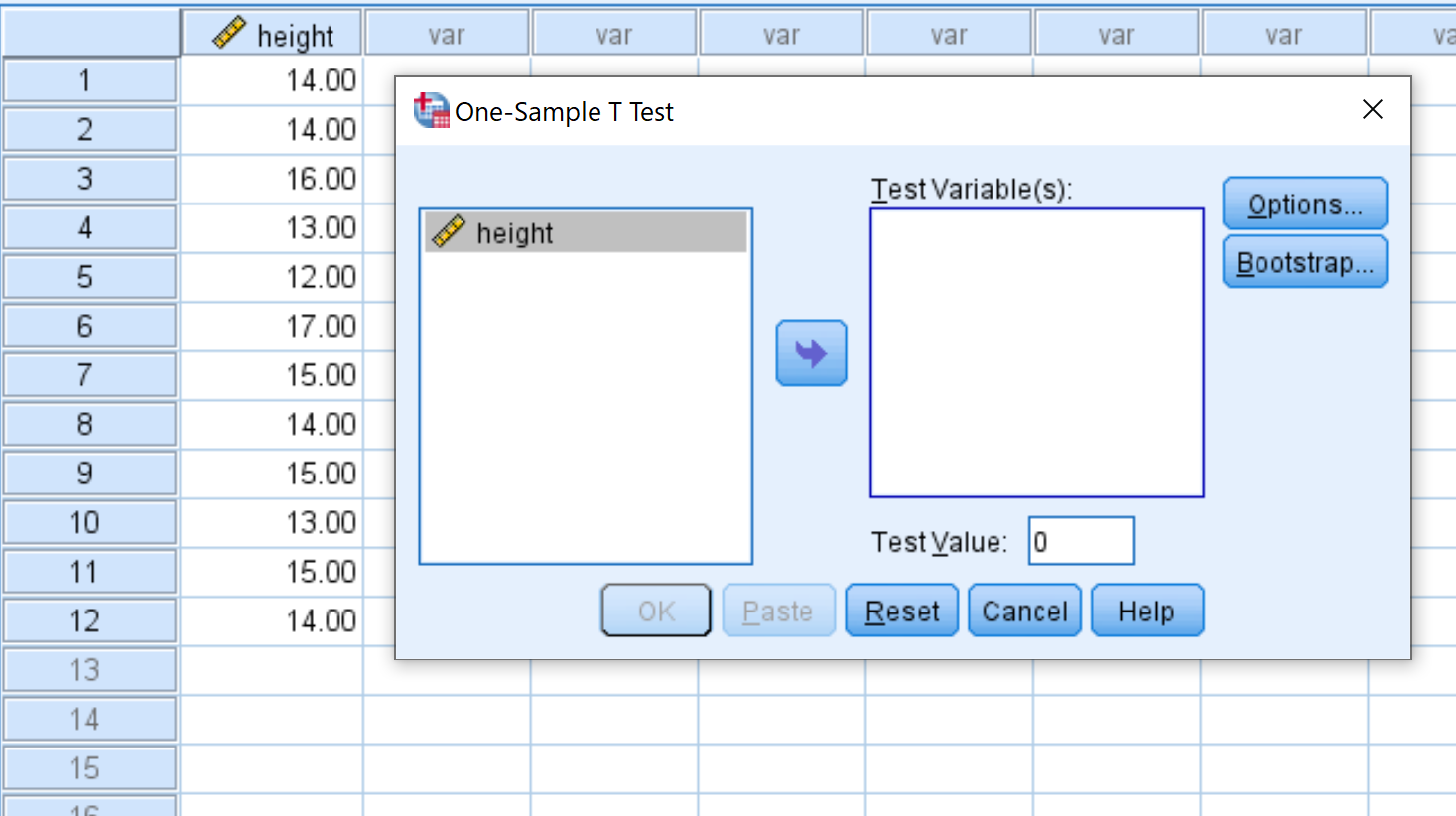
Sleep de hoogte van de variabele naar het vak met de naam Testvariabele(n) en verander de Testwaarde in 15. Klik vervolgens op OK .

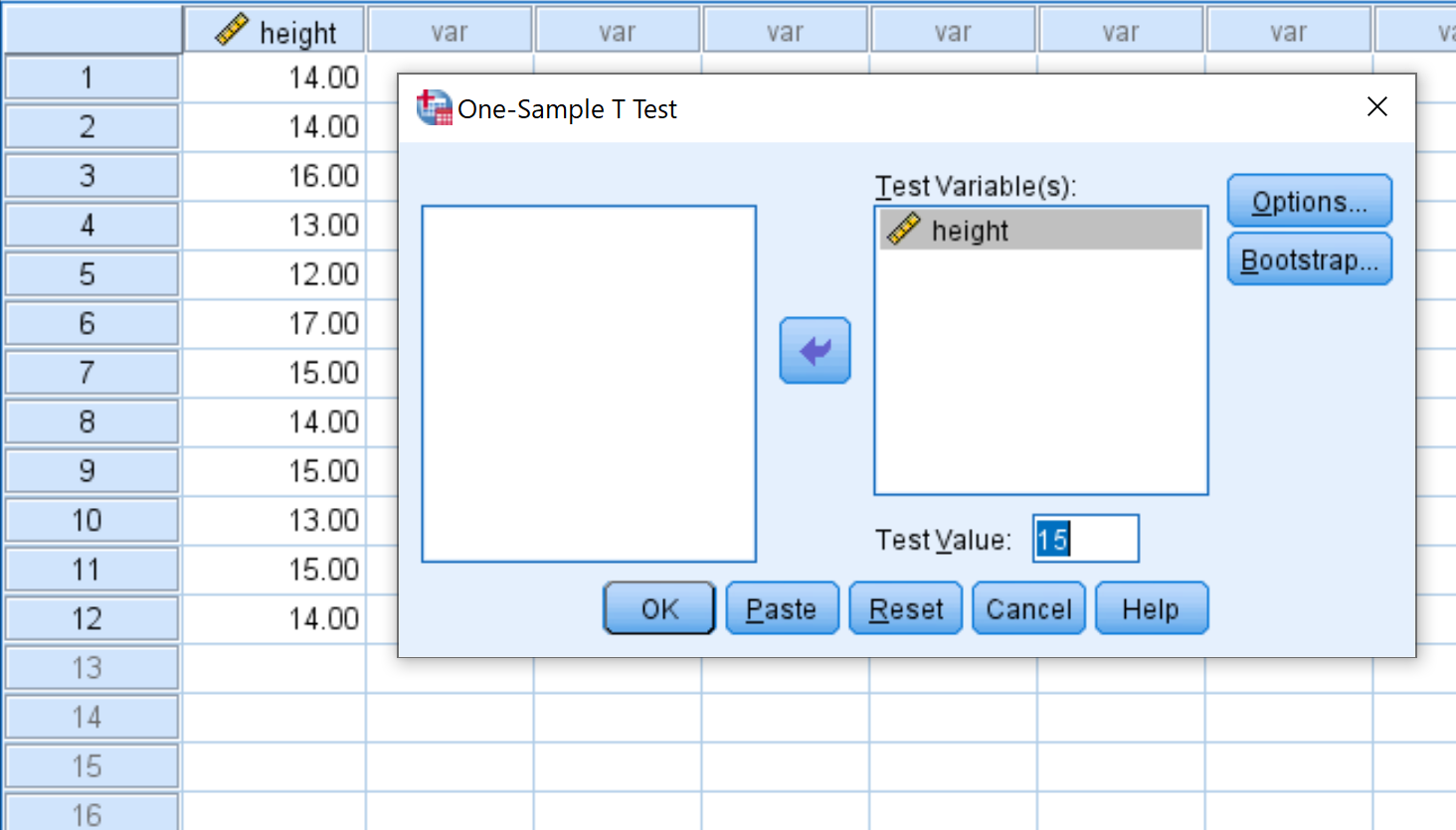
Stap 3: Interpreteer de resultaten.

Zodra u op OK klikt, worden de t-testresultaten met één monster weergegeven:

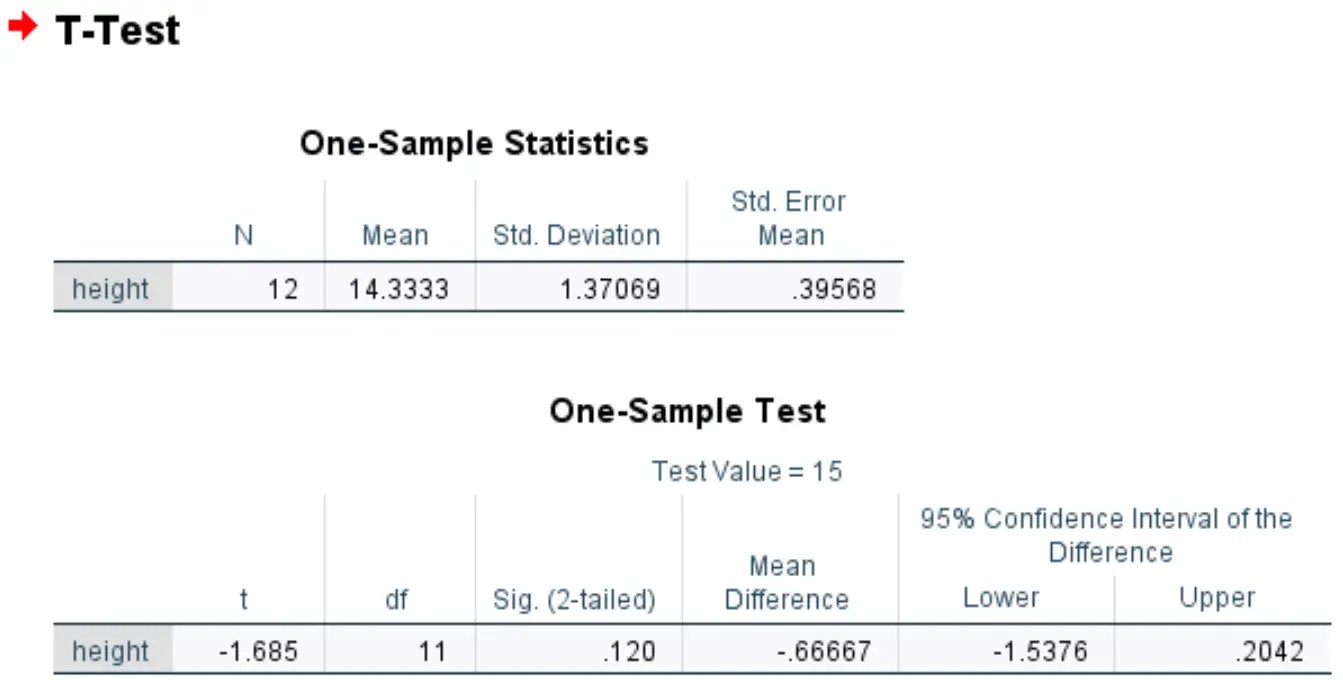
De eerste tabel toont samenvattende statistieken voor variabele hoogte:

• N: Steekproefomvang
• Gemiddeld: de gemiddelde hoogte van de planten in het monster
• Standaard. Afwijking: De standaardafwijking van de planthoogte in het monster.
• Standaard. Gemiddelde fout: de standaardfout van het gemiddelde, berekend als s/√n

De tweede tabel toont de resultaten van de one-sample t-test:

• t: De teststatistiek, berekend als (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
• df: De vrijheidsgraden, berekend als n-1 = 12-1 = 11
• Zig. (tweezijdig): De tweezijdige p-waarde die overeenkomt met een waarde van -1,685 met df=11
• Gemiddeld verschil: het verschil tussen het steekproefgemiddelde en het hypothetische gemiddelde
• 95% BI van verschil: 95% betrouwbaarheidsinterval voor het werkelijke verschil tussen het steekproefgemiddelde en het hypothetische gemiddelde.

Omdat de p-waarde van de test (0,120) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat de werkelijke gemiddelde hoogte van deze plantensoort iets anders is dan 15 inch.