Hoe u een qq-plot maakt in excel

Een QQ-plot , een afkorting van „quantile-quantile“, wordt vaak gebruikt om te evalueren of een dataset mogelijk afkomstig is van een theoretische distributie. In de meeste gevallen wordt dit type plot gebruikt om te bepalen of een dataset al dan niet een normale verdeling volgt.

In deze zelfstudie wordt uitgelegd hoe u een QQ-plot voor een gegevensset in Excel maakt.

Voorbeeld: QQ-plot in Excel

Voer de volgende stappen uit om een QQ-plot voor een gegevensset te maken.

Stap 1: Voer de gegevens in en sorteer ze.

Voer de volgende gegevens in een kolom in:

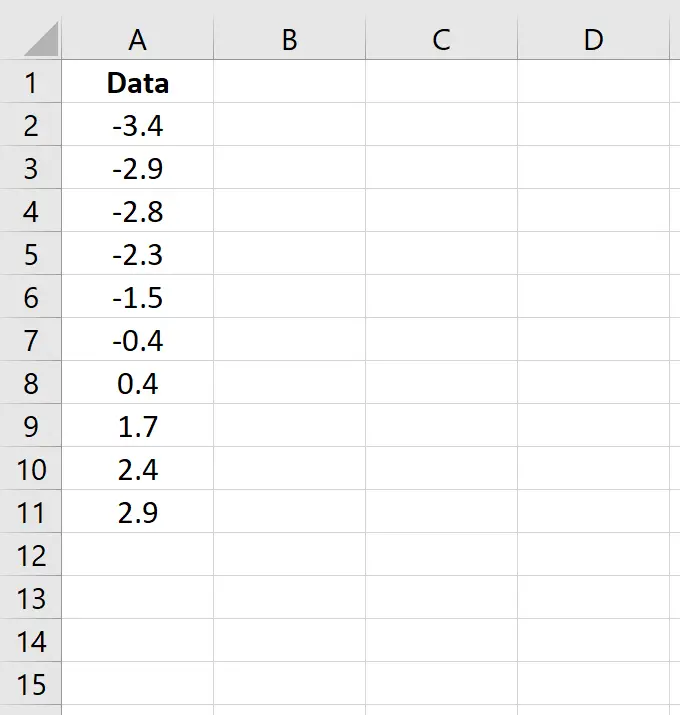
Merk op dat deze gegevens al zijn gesorteerd van klein naar groot. Als uw gegevens nog niet zijn gesorteerd, gaat u naar het tabblad Gegevens op het bovenste lint in Excel, gaat u vervolgens naar de groep Sorteren en filteren en klikt u vervolgens op het pictogram Sorteren van A tot Z.

Stap 2: Zoek de rangorde van elke gegevenswaarde.

Gebruik vervolgens de volgende formule om de rangorde van de eerste waarde te berekenen:

= RANG (A2, $A$2:$A$11, 1)

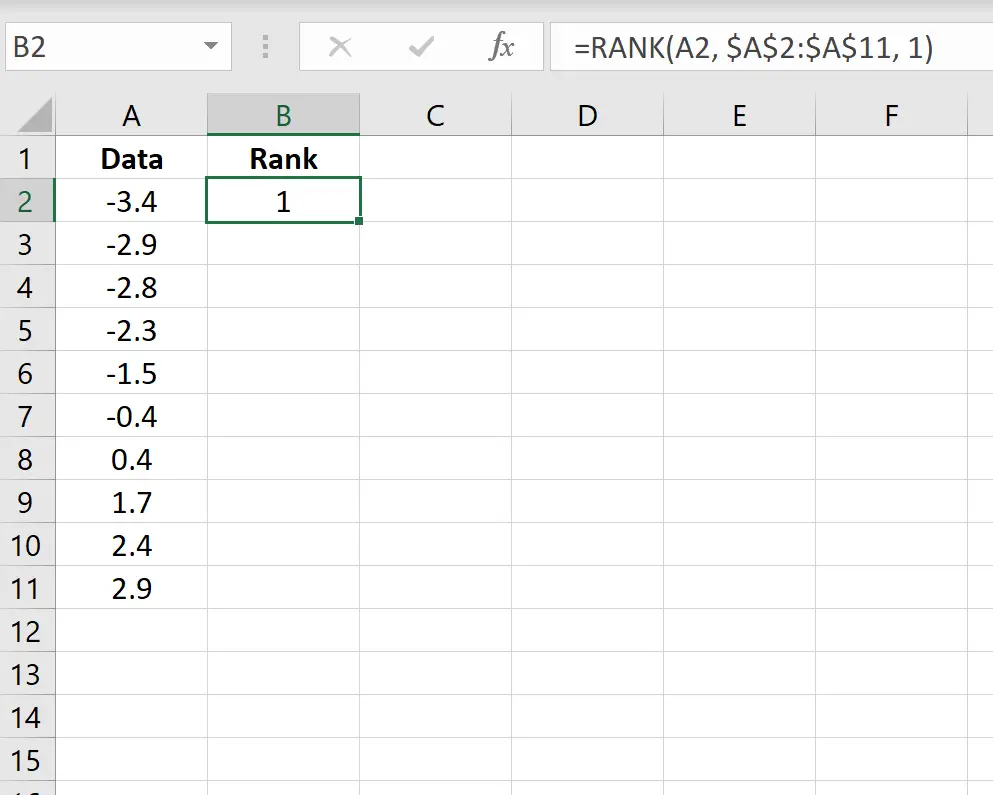
Kopieer deze formule naar alle andere cellen in de kolom:

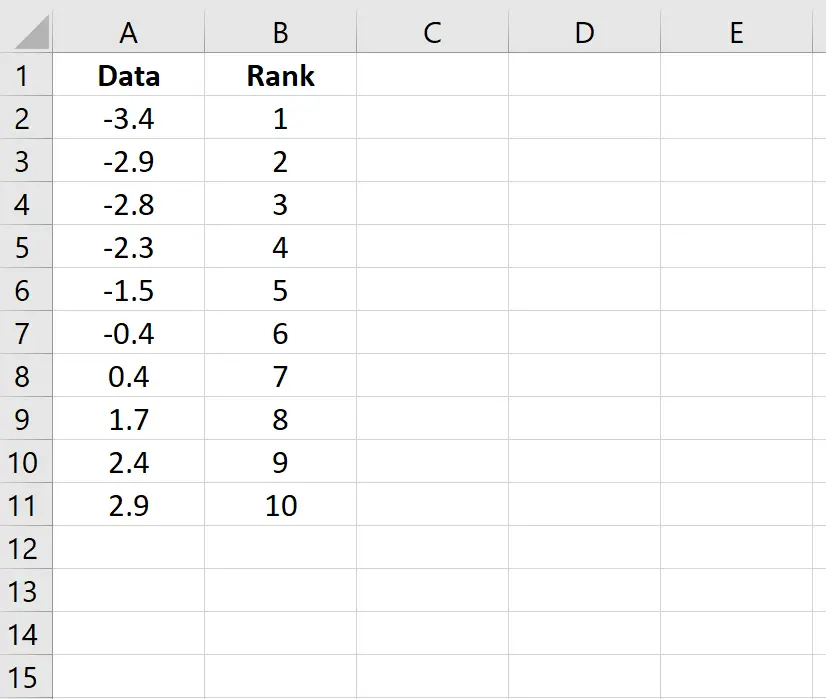
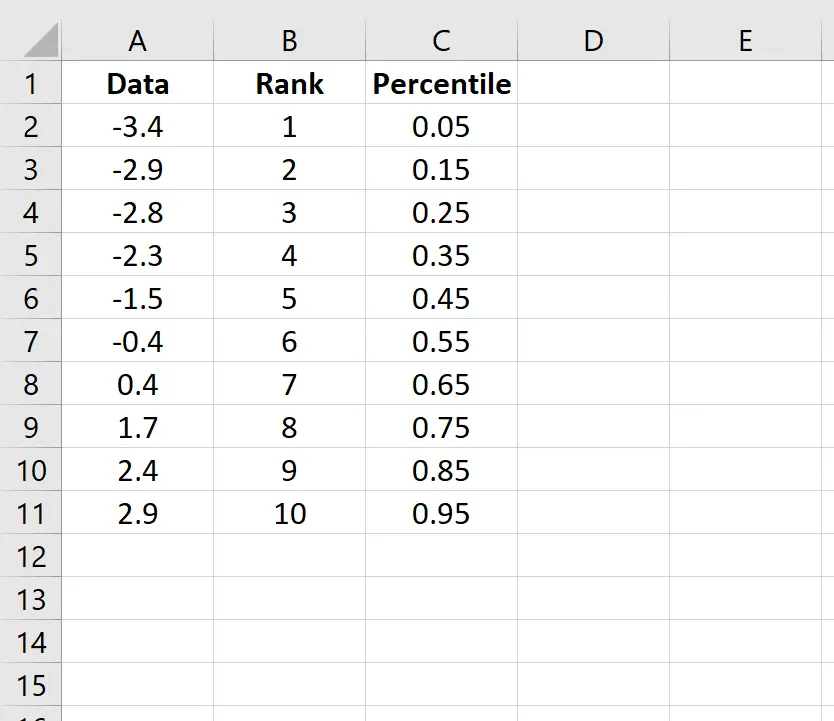
Stap 3: Zoek het percentiel van elke gegevenswaarde.

Gebruik vervolgens de volgende formule om het percentiel van de eerste waarde te berekenen:

=(B2-0,5)/COUNT($B$2:$B$11)

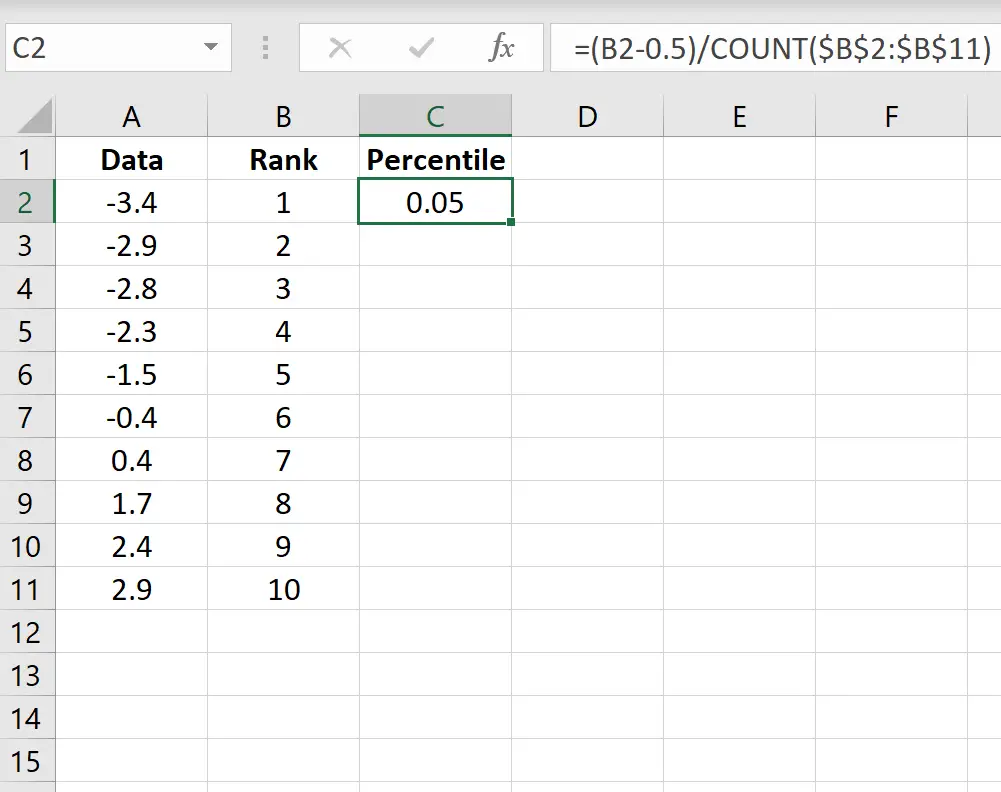
Kopieer deze formule naar alle andere cellen in de kolom:

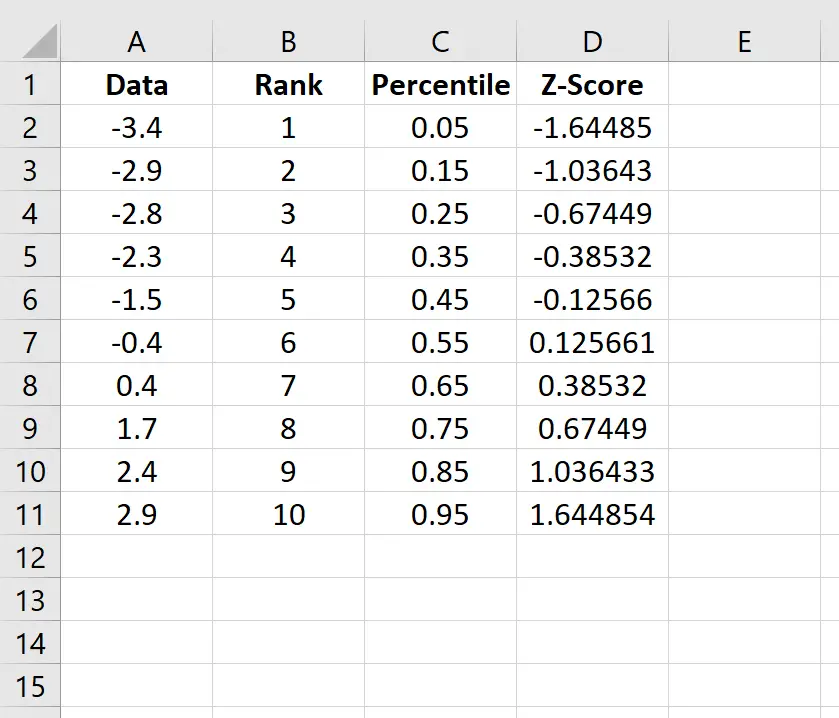
Stap 4: Bereken de z-score voor elke gegevenswaarde.

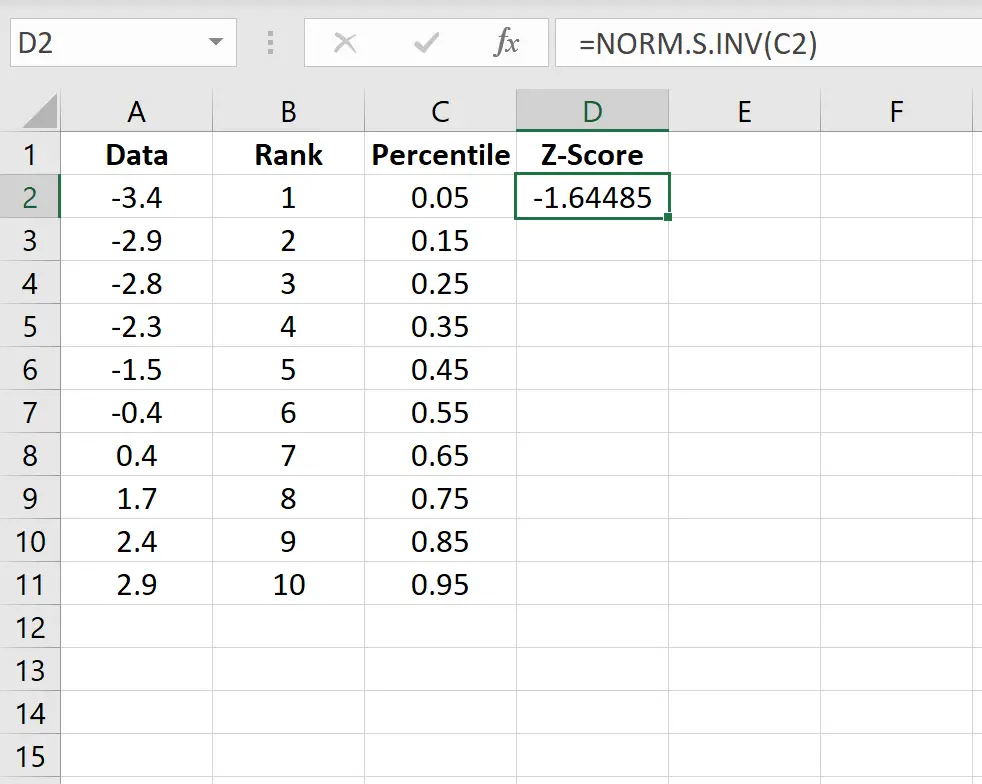
Gebruik de volgende formule om de z-score voor de eerste gegevenswaarde te berekenen:

=NORM.S.INV(C2)

Kopieer deze formule naar alle andere cellen in de kolom:

Stap 5: Maak de QQ-plot.

Kopieer de originele gegevens van kolom A naar kolom E en markeer vervolgens de gegevens in kolommen D en E.

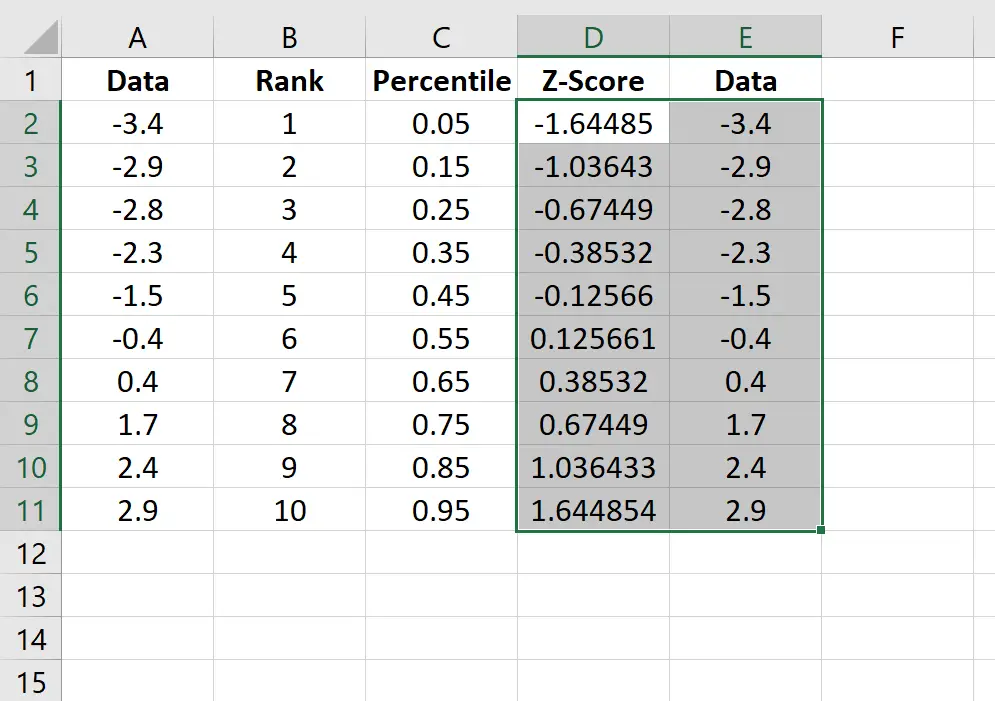
Ga langs het bovenste lint naar Invoegen . Kies in de groep Afbeeldingen de optie Spreiding invoegen (X, Y) en klik op de optie Spreiding . Dit levert de volgende QQ-plot op:

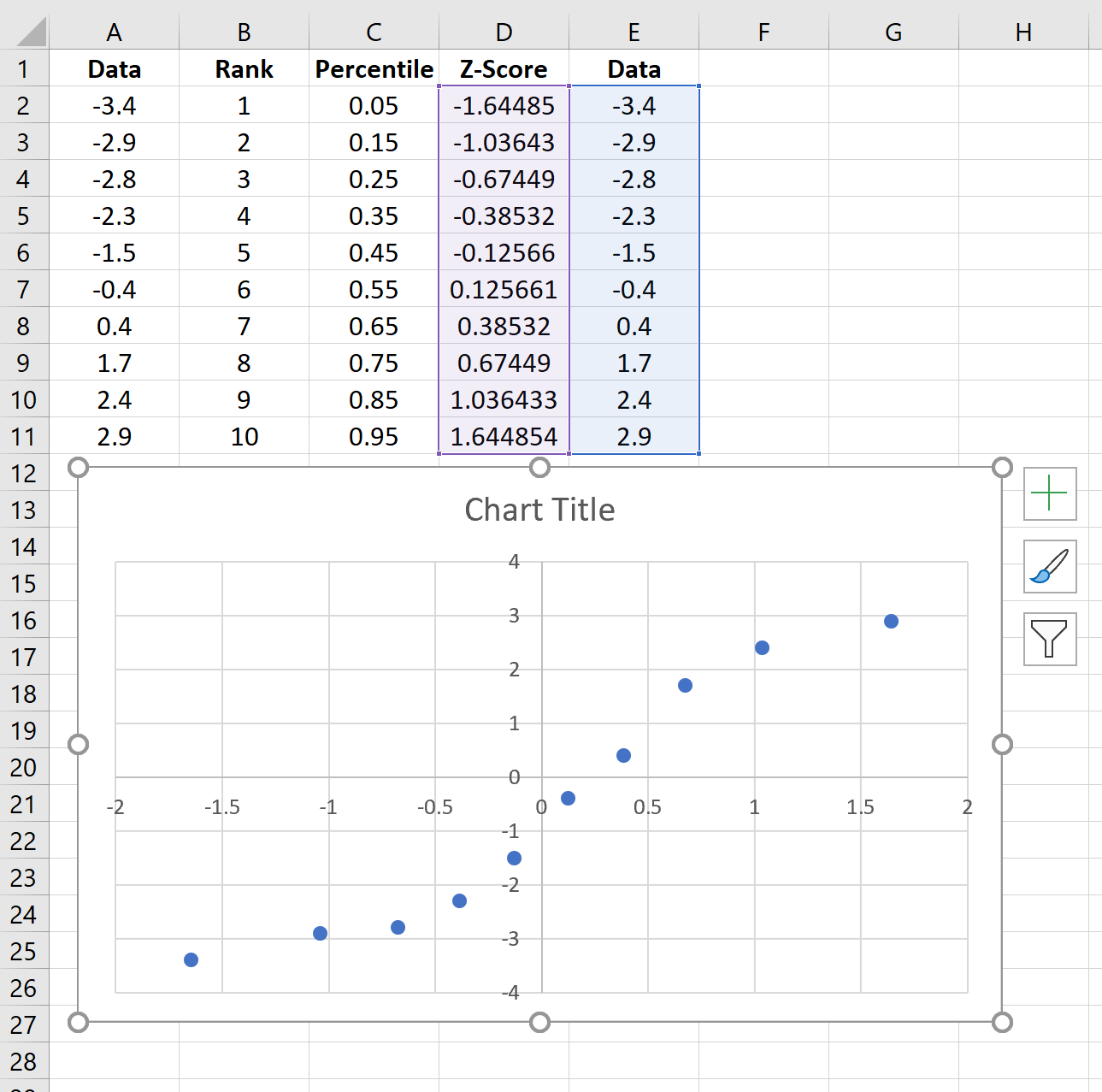
Klik op het plusteken in de rechterbovenhoek van het diagram en vink het vakje naast Trendlijn aan. Hierdoor wordt de volgende regel aan het diagram toegevoegd:

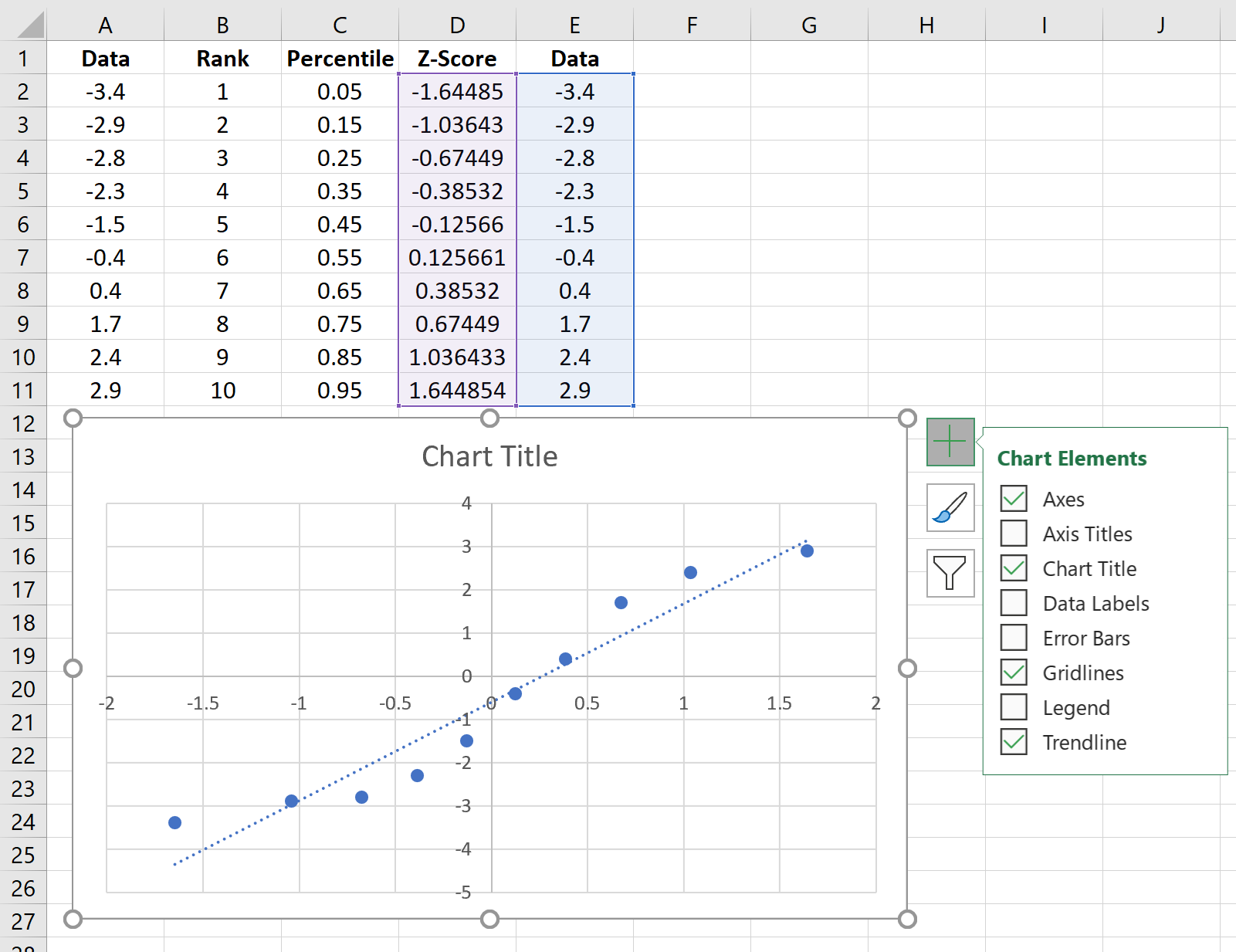
Voel je vrij om labels toe te voegen voor de titel en assen van het diagram om het esthetischer te maken:

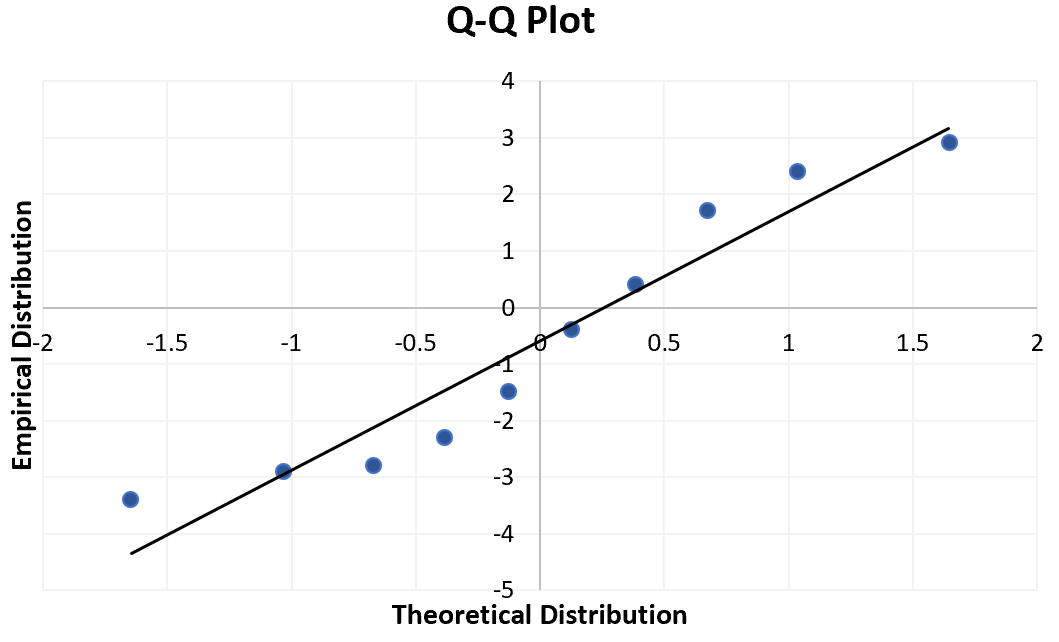
De manier om een QQ-plot te interpreteren is eenvoudig: als de gegevenswaarden een ruwweg rechte lijn volgen in een hoek van 45 graden, dan zijn de gegevens normaal verdeeld. We kunnen in onze QQ-grafiek hierboven zien dat de gegevenswaarden de neiging hebben iets af te wijken van de 45 graden-lijn, vooral aan de uiteinden, wat erop zou kunnen wijzen dat de gegevensset niet normaal verdeeld is.

Hoewel een QQ-plot geen formele statistische test is, biedt het een eenvoudige manier om visueel te controleren of een dataset normaal verdeeld is of niet.