Hoe u een qq-plot maakt in python

Een QQ-plot , een afkorting van „quantile-quantile“, wordt vaak gebruikt om te evalueren of een dataset mogelijk afkomstig is van een theoretische distributie.

In de meeste gevallen wordt dit type plot gebruikt om te bepalen of een dataset al dan niet een normale verdeling volgt.

In deze tutorial wordt uitgelegd hoe u een QQ-plot voor een gegevensset in Python maakt.

Voorbeeld: QQ-plot in Python

Stel dat we de volgende gegevensset van 100 waarden hebben:

 import numpy as np

#create dataset with 100 values that follows a normal distribution
np.random.seed(0)
data = np.random.normal(0,1, 1000)

#view first 10 values
data[:10] 

array([ 1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799,
       -0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985 ])

Om een QQ-plot voor deze dataset te maken, kunnen we de functie qqplot() uit de statsmodels-bibliotheek gebruiken:

 import statsmodels.api as sm
import matplotlib.pyplot as plt

#create QQ plot with 45-degree line added to plot
fig = sm.qqplot(data, line='45')
plt.show()

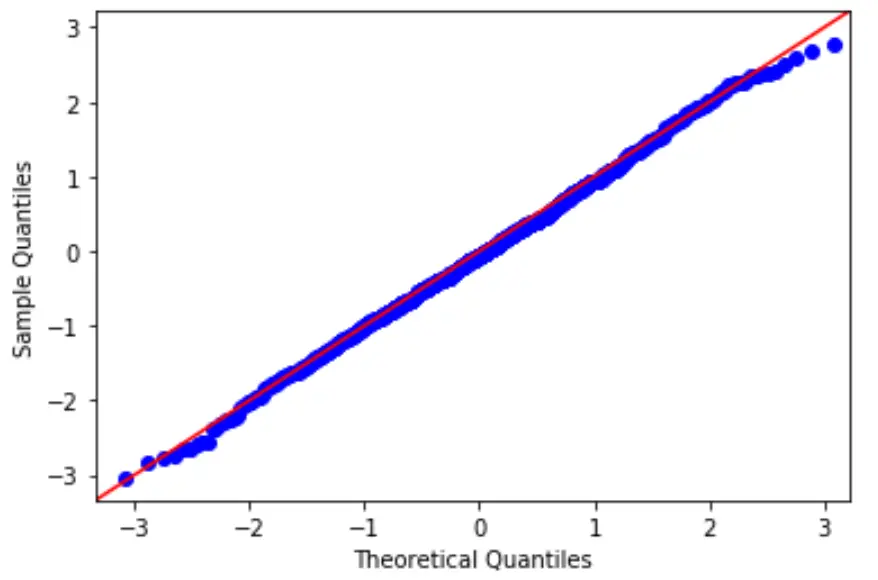
In een QQ-plot geeft de x-as de theoretische kwantielen weer. Dit betekent dat het niet uw werkelijke gegevens toont, maar eerder aangeeft waar uw gegevens zich zouden bevinden als deze normaal verdeeld zouden zijn.

Op de Y-as worden uw huidige gegevens weergegeven. Dit betekent dat als de gegevenswaarden een grofweg rechte lijn volgen in een hoek van 45 graden, de gegevens normaal verdeeld zijn.

We kunnen in onze QQ-grafiek hierboven zien dat de gegevenswaarden de neiging hebben de 45 graden nauw te volgen, wat betekent dat de gegevens waarschijnlijk normaal verdeeld zijn. Dit zou geen verrassing moeten zijn, aangezien we de 100 gegevenswaarden hebben gegenereerd met behulp van de functie numpy.random.normal() .

Overweeg in plaats daarvan of we een dataset van 100 uniform verdeelde waarden hebben gegenereerd en een QQ-plot voor die dataset hebben gemaakt:

 #create dataset of 100 uniformly distributed values
data = np.random.uniform(0,1, 1000)

#generate QQ plot for the dataset
fig = sm.qqplot(data, line='45')
plt.show()

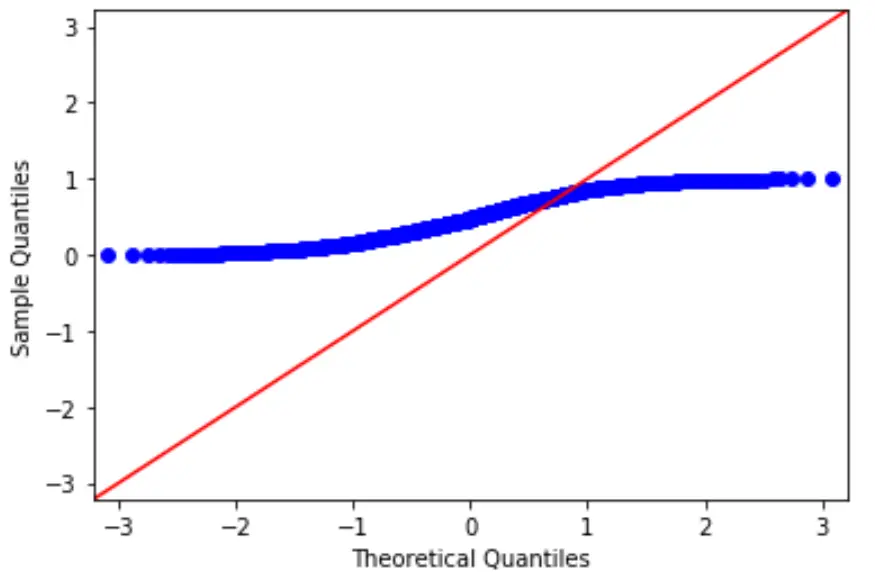
De datawaarden volgen duidelijk niet de rode lijn van 45 graden, wat aangeeft dat ze geen normale verdeling volgen.

Opmerkingen over QQ-plots

Houd rekening met de volgende opmerkingen over QQ-plots:

• Hoewel een QQ-plot geen formele statistische test is, biedt het een eenvoudige manier om visueel te controleren of een dataset normaal verdeeld is of niet.
• Zorg ervoor dat u QQ-plots niet verwart met PP-plots , die minder vaak worden gebruikt en minder nuttig zijn voor het analyseren van gegevenswaarden die aan de staart van de verdeling vallen.

Meer Python-tutorials vind je hier .