Hoe u een t-test met één monster uitvoert in sas

Een one-sample t-test wordt gebruikt om te bepalen of een populatiegemiddelde al dan niet gelijk is aan een bepaalde waarde.

In deze zelfstudie wordt uitgelegd hoe u een t-test met één monster uitvoert in SAS.

Voorbeeld: een voorbeeld-t-test in SAS

Stel dat een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. Ze neemt een willekeurig monster van twaalf planten en registreert hun hoogte in centimeters.

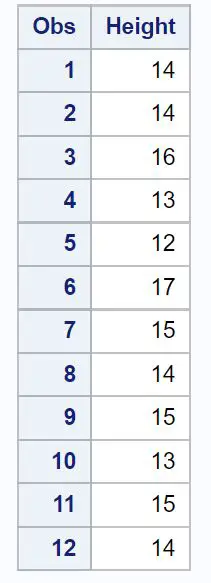
De hoogtes zijn: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14

Gebruik de volgende stappen om een t-test met één monster uit te voeren om te bepalen of de gemiddelde hoogte van deze plantensoort daadwerkelijk 15 inch is.

Stap 1: Creëer de gegevens.

Eerst zullen we de volgende code gebruiken om de gegevensset in SAS te maken:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

Stap 2: Voer een t-test met één monster uit.

Vervolgens gebruiken we proc ttest om de t-test uit te voeren op een voorbeeld:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

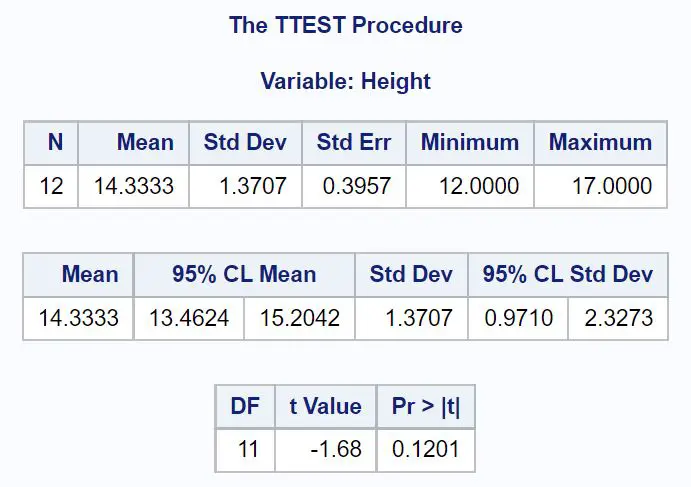
De eerste tabel toont beschrijvende statistieken voor onze steekproef, waaronder:

• N (totaal aantal waarnemingen): 12
• Gemiddelde (steekproefgemiddelde): 14,3333
• Std Dev (standaardafwijking van het monster): 1,3707
• Standaardfout (standaardfout, berekend als s/ √n ): 0,3957
• Minimum (de minimumwaarde): 12
• Maximaal (de maximale waarde) 17

De tweede tabel toont het 95% betrouwbaarheidsinterval voor het werkelijke populatiegemiddelde:

• 95% BI voor μ: [13,4624, 15,2042]

De derde tabel toont de t-teststatistiek en de bijbehorende p-waarde:

• t-teststatistiek: -1,68
• p-waarde: 0,1201

Opmerking : de teststatistiek werd als volgt berekend:

• t-teststatistiek = ( x – μ) / (s/ √n )
• t-teststatistiek = (14,3333-15) / (1,3707/√ 12 )
• t-teststatistiek = -1,68

Bedenk dat de t-test met één steekproef de volgende nul- en alternatieve hypothesen gebruikt:

• _H0 : μ = 15 inch
• H _A : μ ≠ 15 inch

Omdat de p-waarde ( .1201 ) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de gemiddelde hoogte van sommige plantensoorten anders is dan 45 centimeter.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere algemene statistische tests in SAS kunt uitvoeren:

Hoe u een door Wilcoxon ondertekende rangtest uitvoert in SAS
Eenrichtings-ANOVA uitvoeren in SAS