Een t-test met één monster uitvoeren op een ti-84-rekenmachine

Een one-sample t-test wordt gebruikt om te testen of het gemiddelde van een populatie gelijk is aan een bepaalde waarde.

In deze tutorial wordt uitgelegd hoe u een t-test met één steekproef uitvoert op een TI-84-rekenmachine.

Voorbeeld: een voorbeeld-t-test op een TI-84-rekenmachine

Onderzoekers willen weten of een bepaald type auto een snelheid van 20 mijl per gallon haalt of niet. Ze nemen een willekeurige steekproef van 74 auto’s en ontdekken dat het gemiddelde 21,29 mpg is, terwijl de standaardafwijking 5,78 mpg is. Gebruik deze gegevens om een t-test met één monster uit te voeren om te bepalen of het werkelijke mpg voor dit type auto gelijk is aan 20 mpg.

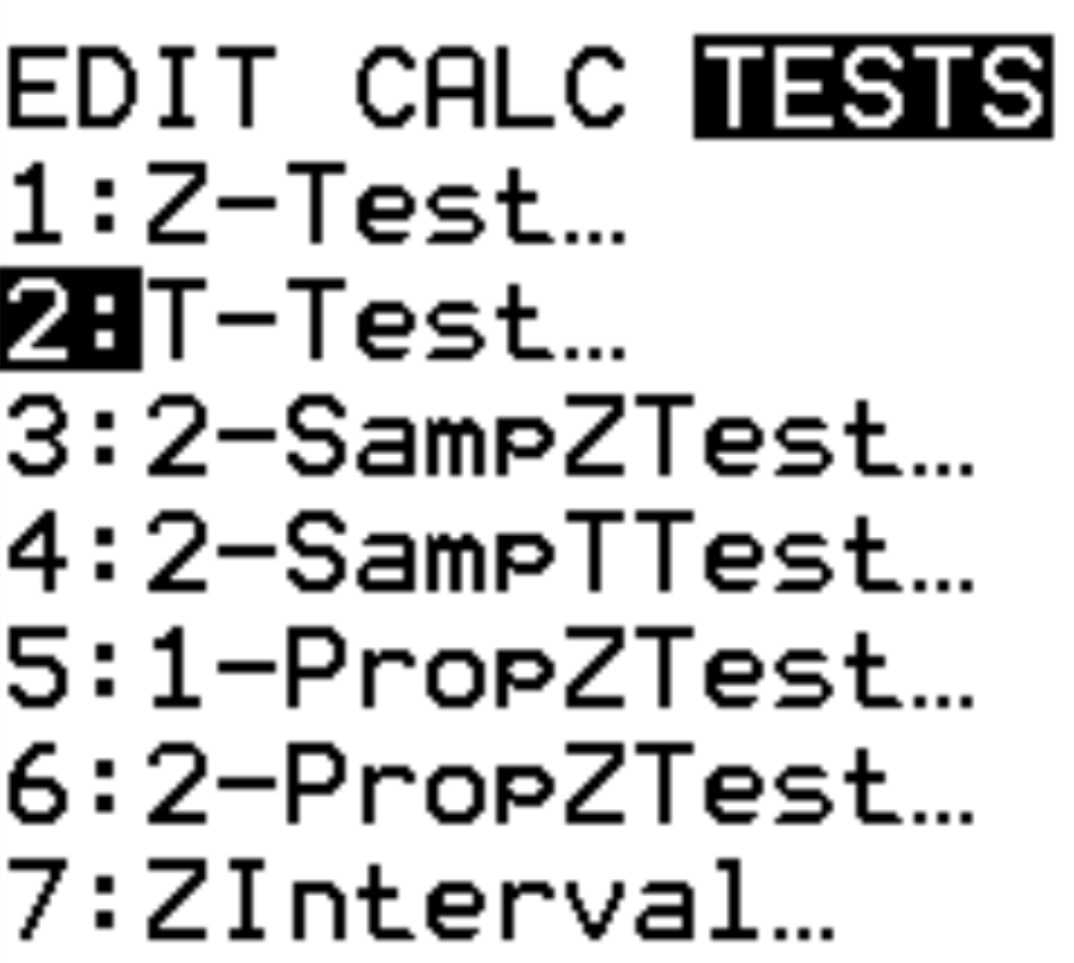
Stap 1: Selecteer T-test.

Tik op Stat . Scroll naar beneden naar TESTEN. Blader naar T-Test en druk op ENTER .

Stap 2: Vul de benodigde gegevens in.

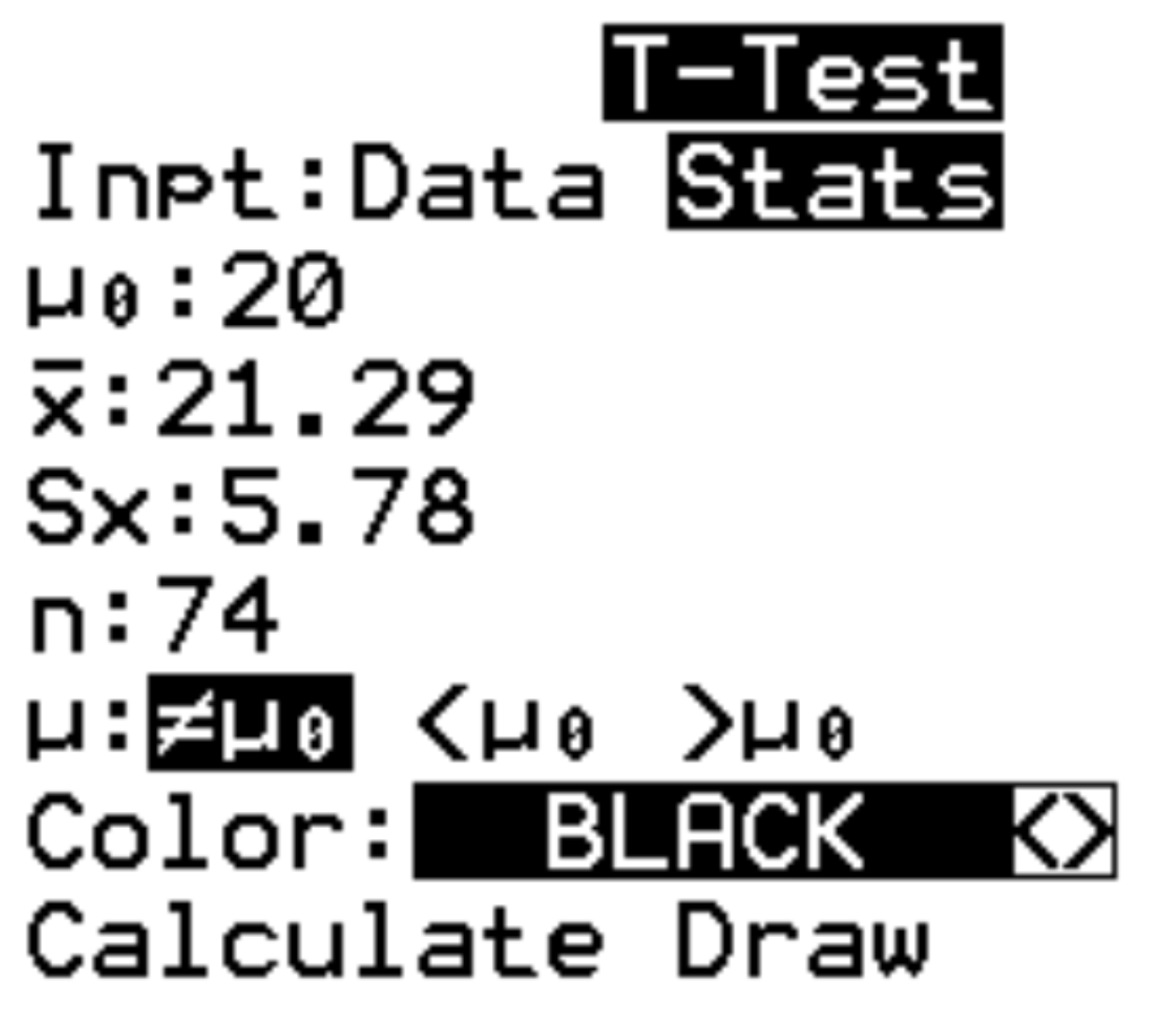
De rekenmachine vraagt om de volgende informatie:

• Invoer: Kies of u met ruwe gegevens (Data) of samenvattende statistieken (Stats) werkt. In dit geval zullen we Statistieken markeren en op ENTER drukken.
• μ ₀ : Het gemiddelde dat in de nulhypothese moet worden gebruikt. We typen 20 en drukken op ENTER .
• x : De steekproefgemiddelden. We typen 21.29 en drukken op ENTER .
• s _x : De standaardafwijking van het monster. We typen 5.78 en drukken op ENTER .
• n : De steekproefomvang. We typen 74 en drukken op ENTER .
• μ : De alternatieve hypothese die moet worden gebruikt. Omdat we een tweezijdige test uitvoeren, zullen we ≠ μ ₀ markeren en op ENTER drukken. Dit geeft aan dat onze alternatieve hypothese μ≠20 is. De andere twee opties zouden worden gebruikt voor linkertests (<μ ₀ ) en rechtertests (>μ ₀ ).

Markeer ten slotte Bereken en druk op ENTER .

Stap 3: Interpreteer de resultaten.

Onze rekenmachine produceert automatisch de resultaten van de one-sample t-test:

Zo interpreteert u de resultaten:

• μ≠20 : Dit is de alternatieve hypothese van de test.
• t=1,919896124 : Dit is de t-teststatistiek.
• p=0,0587785895 : Dit is de p-waarde die overeenkomt met de teststatistiek.
• x =21,59 . Dit is het gemiddelde monster dat we hebben genomen.
• _sx =5,78 . Dit is de standaarddeviatie van de steekproef die we hebben ingevoerd.
• n=74 : Dit is de steekproefomvang die we hebben ingevoerd.

Omdat de p-waarde van de test (0,0587785895) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de gemiddelde mpg voor dit type auto iets anders is dan 20 mpg.