Kan een z-score negatief zijn?

In de statistiek vertelt een z-score ons hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde . We gebruiken de volgende formule om een z-score te berekenen:

z = (X – μ) / σ

waarbij X de waarde is die we analyseren, μ het gemiddelde is en σ de standaardafwijking.

Een z-score kan positief, negatief of nul zijn.

Een positieve z-score geeft aan dat een bepaalde waarde boven het gemiddelde ligt, een negatieve z-score geeft aan dat een bepaalde waarde onder het gemiddelde ligt, en een z-score van nul geeft aan dat een bepaalde waarde gelijk is aan het gemiddelde.

Een paar voorbeelden moeten dit duidelijk maken.

Voorbeelden: Een Z-score berekenen

Laten we zeggen dat we de volgende gegevensset hebben die de hoogte (in inches) van een bepaalde groep planten weergeeft:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

Het steekproefgemiddelde van deze dataset is 13 en de standaarddeviatie van de steekproef is 5,51 .

1. Zoek de z-score voor de waarde “8” in deze dataset.

Zo berekent u de z-score:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Dit betekent dat de waarde “8” 0,91 standaardafwijkingen lager is dan het gemiddelde.

2. Zoek de z-score voor de waarde “13” in deze dataset.

Zo berekent u de z-score:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Dit betekent dat de waarde “13” exact gelijk is aan het gemiddelde.

3. Zoek de z-score voor de waarde “20” in deze dataset.

Zo berekent u de z-score:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Dit betekent dat de waarde “20” 1,28 standaardafwijkingen boven het gemiddelde ligt.

Hoe Z-scores te interpreteren

De AZ-grafiek vertelt ons welk percentage van de waarden onder bepaalde Z-scores valt. Een paar voorbeelden moeten dit duidelijk maken.

Voorbeeld 1: Negatieve Z-scores

Eerder ontdekten we dat de ruwe waarde ‚8‘ in onze dataset een z-score had van -0,91 . Volgens de Z-tabel is 18,14% van de waarden lager dan deze waarde.

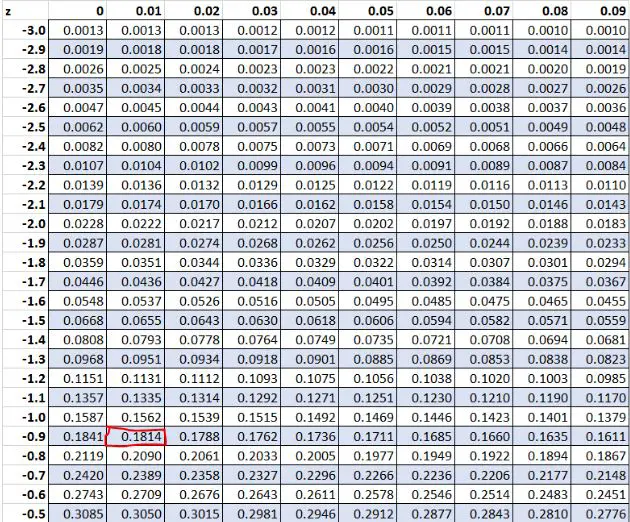
Voorbeeld 2: Z-scores gelijk aan nul

Eerder hebben we ontdekt dat de ruwe waarde „13“ in onze dataset een z-score van 0 had. Volgens de Z-tabel is 50,00% van de waarden kleiner dan deze waarde.

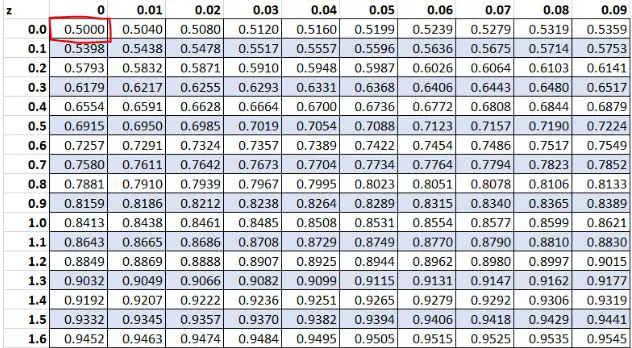
Voorbeeld 3: Positieve Z-scores

Eerder ontdekten we dat de ruwe waarde „20“ in onze dataset een z-score van 1,28 had. Volgens de Z-tabel is 89,97% van de waarden lager dan deze waarde.

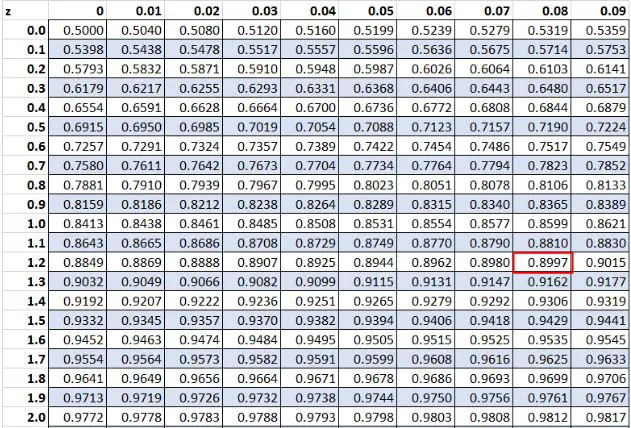
Conclusie

Z-scores kunnen elke waarde aannemen tussen negatief oneindig en positief oneindig, maar de meeste z-scores liggen binnen 2 standaarddeviaties van het gemiddelde. Er bestaat eigenlijk een regel in de statistiek die bekend staat als de vuistregel , die stelt dat voor een gegeven dataset met een normale verdeling:

• 68% van de datawaarden ligt binnen één standaardafwijking van het gemiddelde.
• 95% van de gegevenswaarden ligt binnen twee standaarddeviaties van het gemiddelde.
• 99,7% van de gegevenswaarden vallen binnen drie standaarddeviaties van het gemiddelde.

Hoe hoger de absolute waarde van een z-score, hoe verder een ruwe waarde verwijderd is van het gemiddelde van de dataset. Hoe lager de absolute waarde van een z-score, hoe dichter een ruwe waarde bij het gemiddelde van de dataset ligt.

Gerelateerde onderwerpen:

Rekenmachine met vuistregels
Hoe de vuistregel toe te passen in Excel