Wat is een monotone relatie? (definitie + voorbeelden)

In de statistiek verwijst een monotone relatie tussen twee variabelen naar een scenario waarin een verandering in de ene variabele gewoonlijk gepaard gaat met een verandering in een specifieke richting in een andere variabele.

Er zijn twee soorten monotone relaties:

Positief monotoon: wanneer de waarde van de ene variabele toeneemt, neigt de waarde van de andere variabele ook toe te nemen.

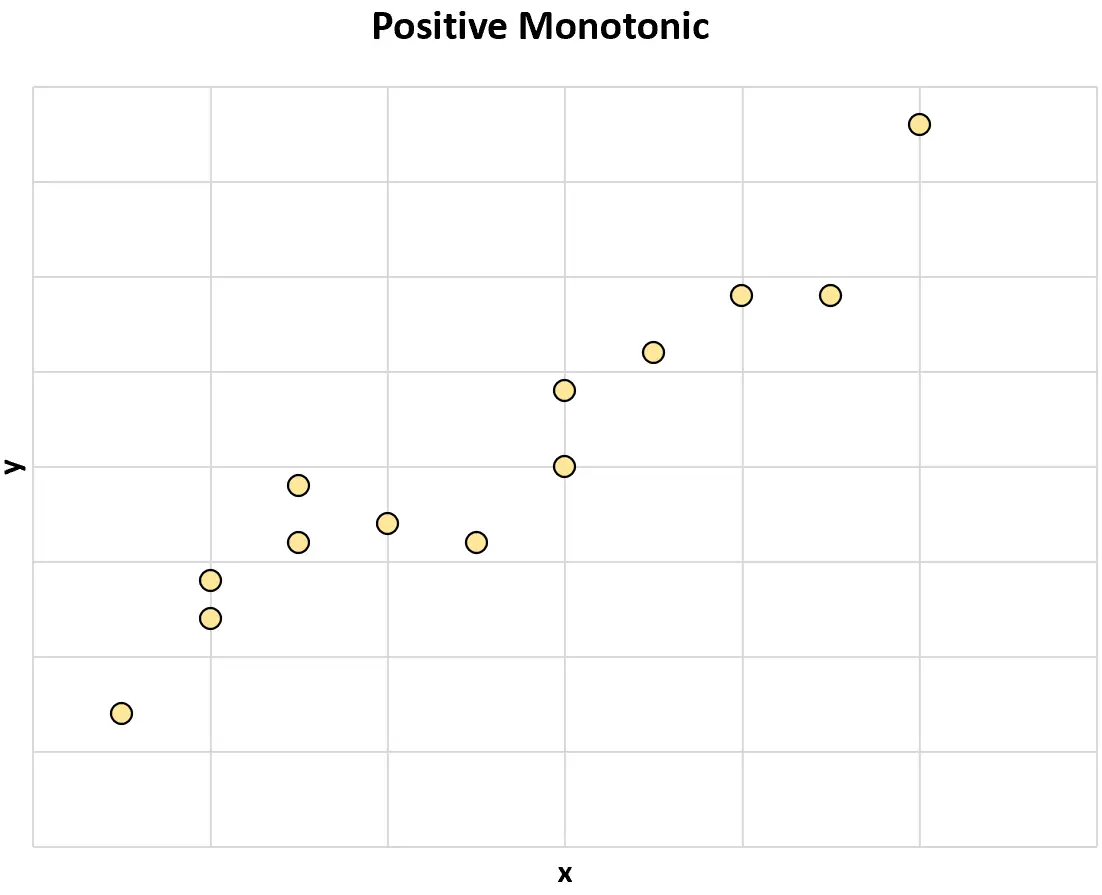
Negatief monotoon: wanneer de waarde van de ene variabele toeneemt, heeft de waarde van de andere variabele de neiging te dalen.

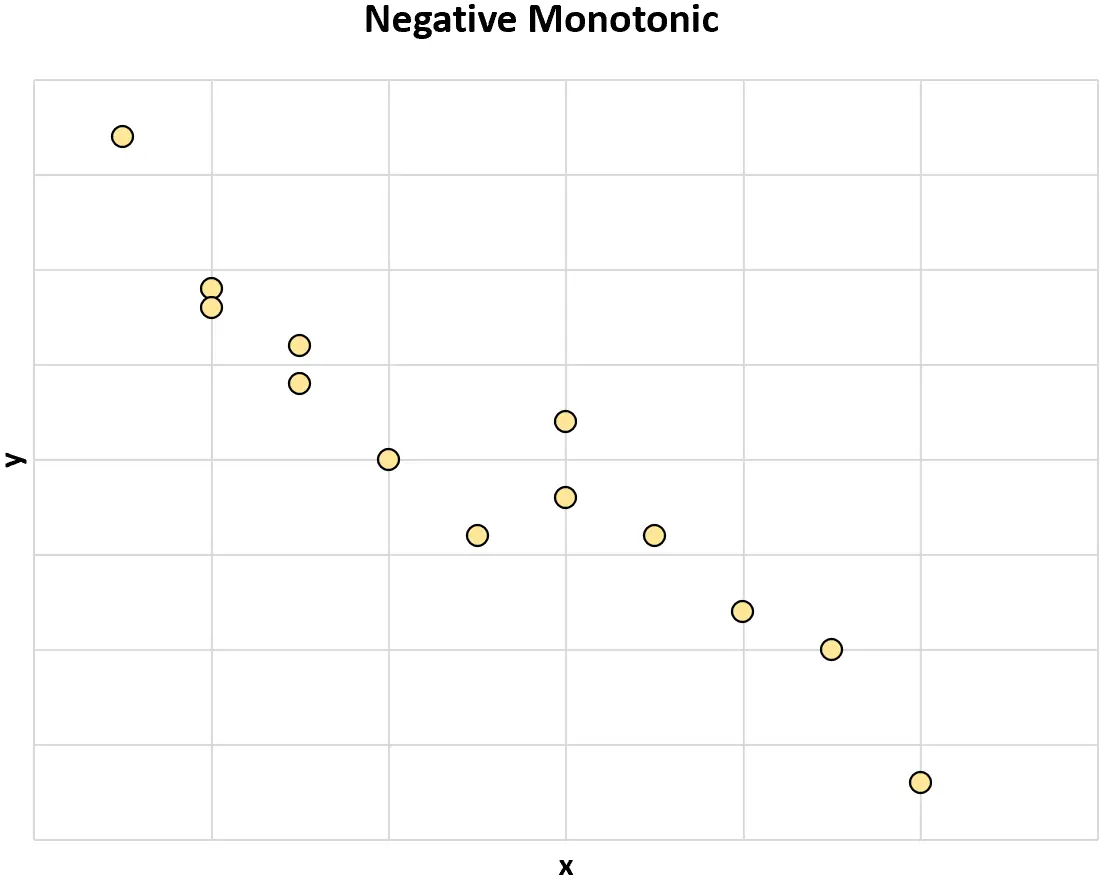
Als twee variabelen over het algemeen niet in dezelfde richting veranderen, wordt er gezegd dat ze een niet-monotone relatie hebben.

Hier is een voorbeeld van een niet-monotone relatie tussen twee variabelen:

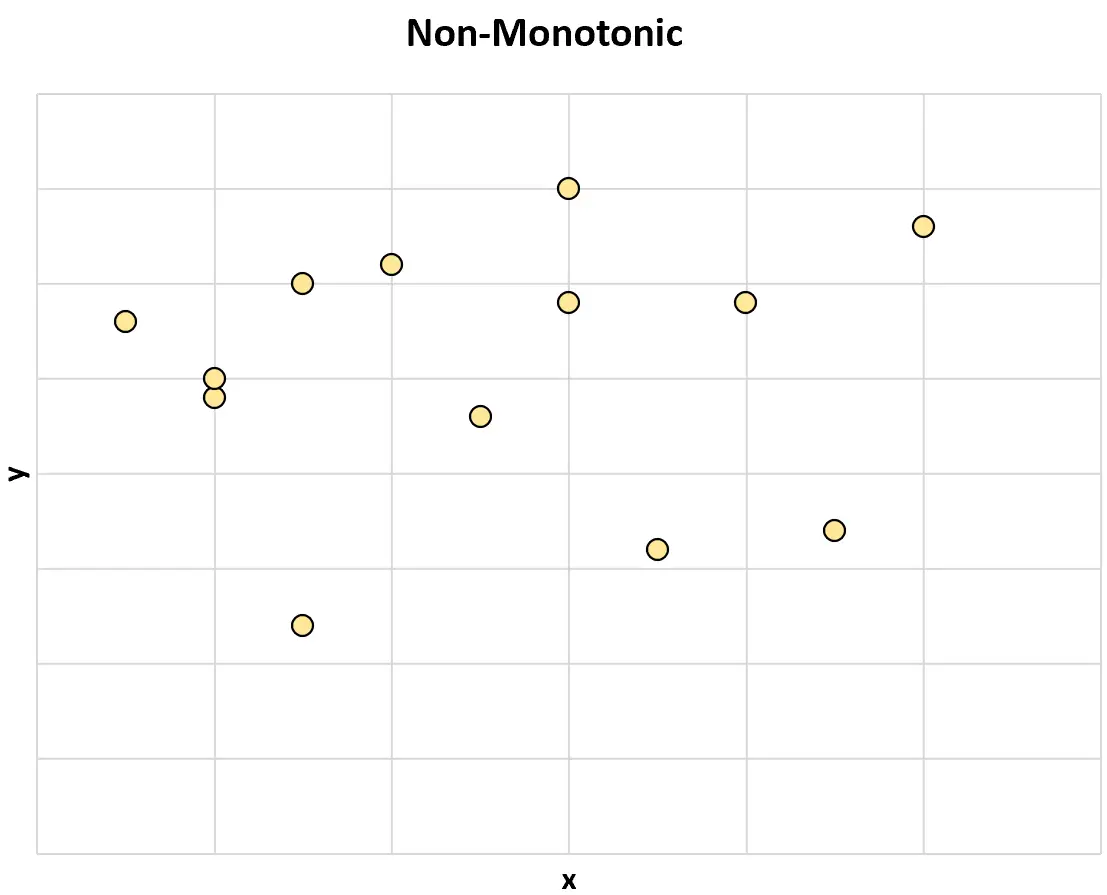
En hier is nog een voorbeeld van een niet-monotone relatie tussen twee variabelen:

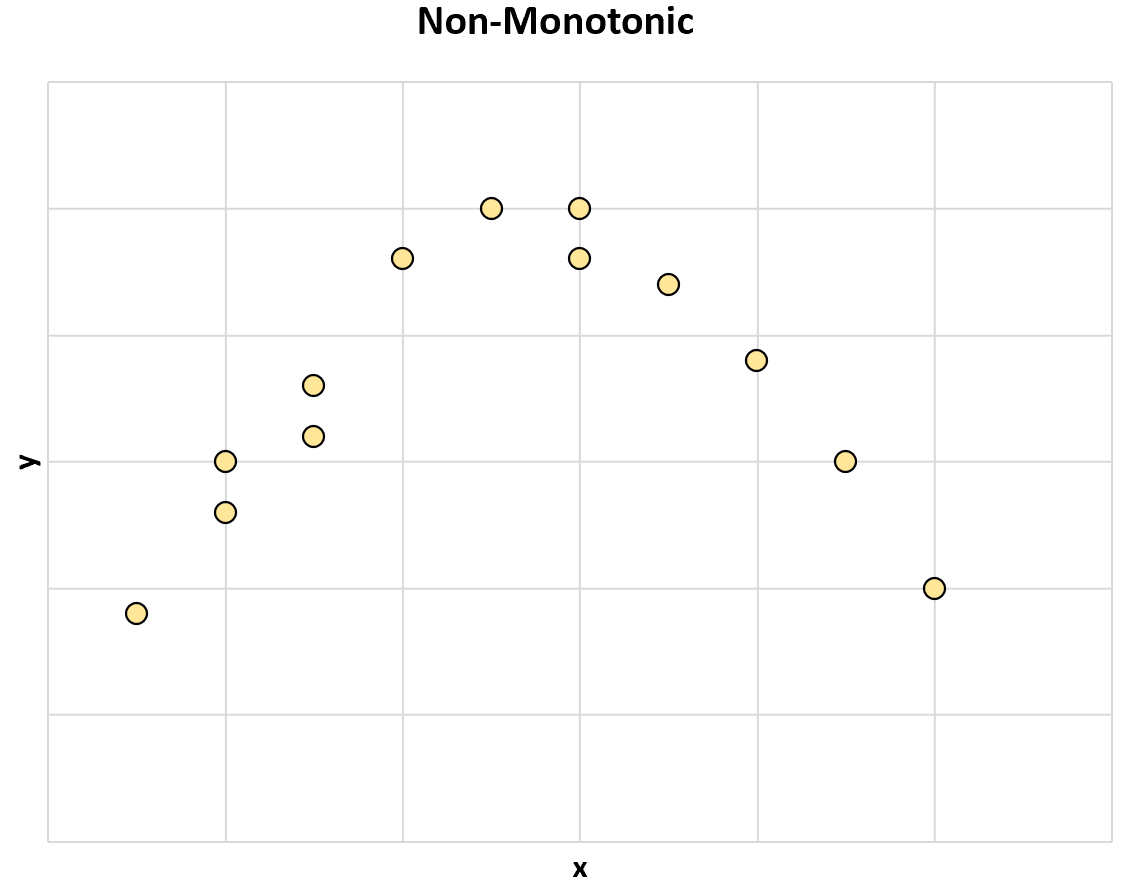
Naarmate de waarde van x toeneemt, neemt de waarde van y soms toe, maar soms neemt de waarde van y af .

Strikt eentonig of niet strikt eentonig

Van twee variabelen wordt gezegd dat ze een strikt monotone relatie hebben als veranderingen in de ene variabele altijd gepaard gaan met een verandering in dezelfde richting in een andere variabele.

De volgende grafiek illustreert bijvoorbeeld een strikt positieve monotone relatie tussen twee variabelen:

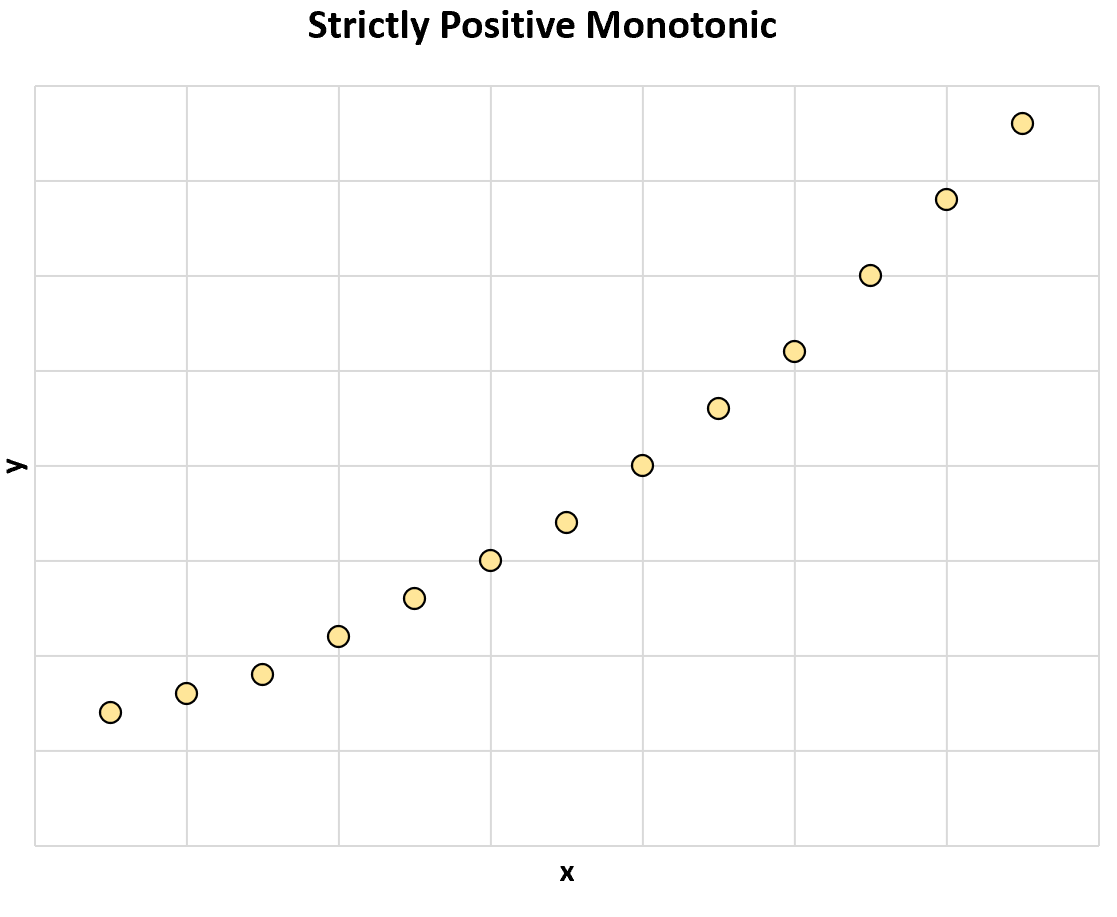
Naarmate de waarde van x toeneemt, neemt de waarde van y altijd toe.

De volgende grafiek illustreert een strikt negatieve monotone relatie tussen twee variabelen:

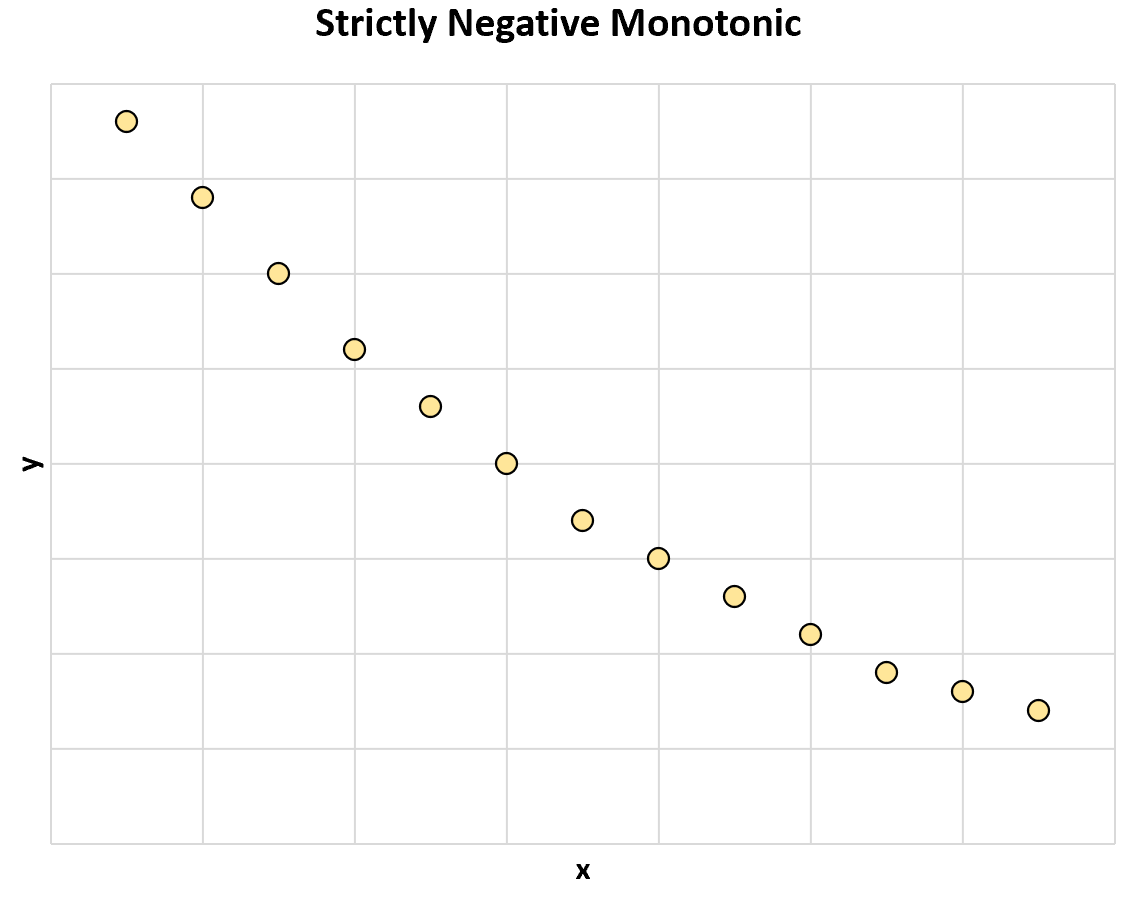
Naarmate de waarde van x toeneemt, neemt de waarde van y altijd af.

Hoe monotone relaties te kwantificeren

De meest gebruikelijke manier om de relatie tussen twee variabelen te kwantificeren is door dePearson-correlatiecoëfficiënt te gebruiken, die de lineaire associatie tussen twee variabelen meet.

Deze coëfficiënt heeft altijd een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Hoe dichter de coëfficiënt bij 1 ligt, hoe sterker de positieve relatie tussen twee variabelen. Omgekeerd geldt: hoe dichter de coëfficiënt bij -1 ligt, hoe sterker de negatieve relatie tussen twee variabelen.

Als de relatie tussen twee variabelen echter monotoon maar niet-lineair is (zoals een exponentiële relatie), dan is het een goed idee om de Spearman Rank-correlatie te gebruiken, die is ontworpen om monotone relaties goed aan te kunnen.

Ongeacht welk type correlatiecoëfficiënt u berekent, het is altijd een goed idee om een spreidingsdiagram te maken om ook de relatie tussen variabelen te visualiseren.