Eenvoudige lineaire regressie

In dit artikel wordt uitgelegd wat eenvoudige lineaire regressie in de statistiek is en hoe deze wordt uitgevoerd. Op dezelfde manier vindt u online een eenvoudige lineaire regressie-oefening opgelost en bovendien een eenvoudige lineaire regressiecalculator.

Wat is eenvoudige lineaire regressie?

Eenvoudige lineaire regressie is een statistisch model dat wordt gebruikt om een onafhankelijke variabele met elkaar in verband te brengen en we proberen de relatie tussen de twee variabelen te benaderen.

Daarom wordt eenvoudige lineaire regressie gebruikt om een vergelijking te vinden die twee variabelen lineair met elkaar in verband brengt. Logischerwijs moet de relatie tussen de twee variabelen lineair zijn, anders moet een ander type regressiemodel worden gebruikt.

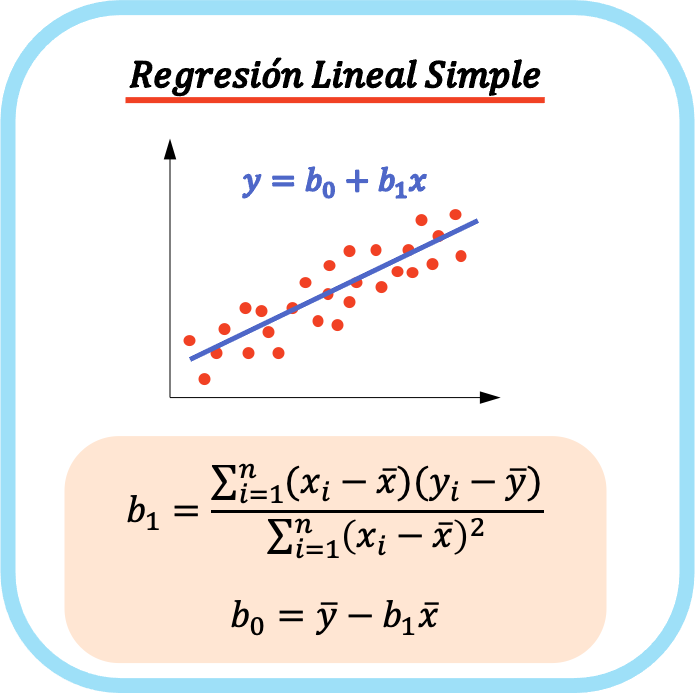
De vergelijking van een eenvoudig lineair regressiemodel bestaat uit twee coëfficiënten: de constante van de vergelijking (b ₀ ) en de correlatiecoëfficiënt tussen de twee variabelen (b ₁ ). Daarom is de vergelijking voor een eenvoudig lineair regressiemodel y=b ₀ +b ₁ x.

De vergelijking voor een eenvoudige lineaire regressie wordt weergegeven als een rechte lijn, dus de coëfficiënt b ₀ is het snijpunt en de coëfficiënt b ₁ is de helling van de lijn.

Eenvoudige lineaire regressieformules

De formules voor het berekenen van de coëfficiënten van een eenvoudige lineaire regressie zijn als volgt:

👉 U kunt de onderstaande rekenmachine gebruiken om de coëfficiënten van een eenvoudige lineaire regressie voor elke gegevensset te berekenen.

Het is duidelijk dat de vergelijking die voortkomt uit het eenvoudige lineaire regressiemodel niet in staat zal zijn de exacte waarde van alle waarnemingen te raden, aangezien dit model eenvoudigweg probeert een vergelijking te vinden die de relatie tussen de twee variabelen benadert. Het residu wordt dus gedefinieerd als het verschil tussen de werkelijke waarde en de waarde die wordt geschat door het lineaire regressiemodel.

Merk op dat het doel van een eenvoudig lineair regressiemodel is om de kwadraten van de residuen te minimaliseren, dat wil zeggen dat eenvoudige lineaire regressie gebaseerd is op het criterium van de kleinste kwadraten .

Concreet voorbeeld van een eenvoudige lineaire regressie

Om het begrip van de eenvoudige lineaire regressiemethode af te ronden, volgt hier een praktisch stapsgewijs voorbeeld waarin de vergelijking van een eenvoudig lineair regressiemodel wordt berekend op basis van een reeks statistische gegevens.

• Na het examen statistiek werd aan vijf studenten gevraagd hoeveel uren studie ze aan het examen hadden besteed. De gegevens worden weergegeven in de onderstaande tabel. Voer een eenvoudig lineair regressiemodel uit van de verzamelde statistische gegevens om de studie-uren lineair te relateren aan het behaalde cijfer.

Om een eenvoudig lineair regressiemodel uit te voeren moeten we de coëfficiënten b ₀ en b ₁ van de vergelijking bepalen en hiervoor moeten we de formules gebruiken die we in het bovenstaande gedeelte hebben gezien.

Om de eenvoudige lineaire regressieformules toe te passen, moeten we echter eerst het gemiddelde van de onafhankelijke variabele en het gemiddelde van de afhankelijke variabele berekenen:

Nu we de gemiddelden van de variabelen kennen, berekenen we de coëfficiënt b ₁ van het model met behulp van de bijbehorende formule:

Ten slotte berekenen we de coëfficiënt b ₀ van het model met behulp van de bijbehorende formule:

Kort gezegd is de vergelijking voor het eenvoudige lineaire regressiemodel van het probleem:

Hieronder ziet u de grafische weergave van de voorbeeldgegevens, evenals de rechte lijn van het eenvoudige lineaire regressiemodel:

Als we tenslotte de vergelijking van het eenvoudige lineaire regressiemodel hebben berekend, hoeven we alleen nog maar het verkregen resultaat te interpreteren. Hiervoor is het essentieel om de determinatiecoëfficiënt van het regressiemodel te berekenen, hoe dit gebeurt kunt u zien door te zoeken naar het betreffende artikel op onze website.

Eenvoudige lineaire regressie-aannames

Om een eenvoudige lineaire regressie uit te voeren, moet aan de volgende aannames worden voldaan:

• Onafhankelijkheid : de waargenomen residuen moeten onafhankelijk van elkaar zijn. Een gebruikelijke manier om de onafhankelijkheid van het model te garanderen, is door willekeur aan het steekproefproces toe te voegen.
• Homoscedasticiteit : Er moet homogeniteit zijn in de varianties van de residuen, dat wil zeggen dat de variabiliteit van de residuen constant moet zijn.
• Normaliteit : De residuen moeten normaal verdeeld zijn, of met andere woorden, ze moeten een normale verdeling volgen met een gemiddelde van 0.
• Lineariteit – De relatie tussen de onafhankelijke variabele en de afhankelijke variabele moet lineair zijn.

Eenvoudige lineaire regressiecalculator

Sluit voorbeeldgegevens aan op de onderstaande rekenmachine om een eenvoudig lineair regressiemodel tussen twee variabelen in te passen. U moet de gegevensparen scheiden, zodat in het eerste vak alleen de waarden van de onafhankelijke variabele X staan en in het tweede vak alleen de waarden van de afhankelijke variabele Y.

Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Eenvoudige en meervoudige lineaire regressie

Ten slotte zullen we zien wat het verschil is tussen eenvoudige lineaire regressie en meervoudige lineaire regressie, aangezien het twee soorten lineaire regressies zijn die vaak in statistieken worden gebruikt.

Meervoudige lineaire regressie maakt het mogelijk om twee of meer verklarende variabelen wiskundig aan een responsvariabele te koppelen. Dat wil zeggen dat bij meervoudige lineaire regressie een model wordt gemaakt waarin er ten minste twee onafhankelijke variabelen zijn.

Daarom is het verschil tussen eenvoudige lineaire regressie en meervoudige lineaire regressie het aantal onafhankelijke variabelen. Bij eenvoudige lineaire regressie is er slechts één onafhankelijke variabele, terwijl er bij meervoudige lineaire regressie twee of meer onafhankelijke variabelen zijn.