Hoe u eenvoudige lineaire regressie uitvoert in excel

Eenvoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een verklarende variabele, x, en een responsvariabele, y, te begrijpen.

In deze zelfstudie wordt uitgelegd hoe u een eenvoudige lineaire regressie in Excel uitvoert.

Voorbeeld: eenvoudige lineaire regressie in Excel

Stel dat we inzicht willen krijgen in de relatie tussen het aantal uren dat een student voor een examen studeert en het cijfer dat hij voor dat examen krijgt.

Om deze relatie te onderzoeken, kunnen we een eenvoudige lineaire regressie uitvoeren met bestudeerde uren als verklarende variabele en examenscores als responsvariabele.

Voer de volgende stappen in Excel uit om een eenvoudige lineaire regressie uit te voeren.

Stap 1: Voer de gegevens in.

Vul voor het aantal gestudeerde uren en de behaalde examenscore voor 20 studenten de volgende gegevens in:

Stap 2: Visualiseer de gegevens.

Voordat u een eenvoudige lineaire regressie uitvoert, is het handig om een spreidingsdiagram van de gegevens te maken om er zeker van te zijn dat er werkelijk een lineair verband bestaat tussen het aantal gestudeerde uren en de examenscore.

Markeer de gegevens in de kolommen A en B. Navigeer op het bovenste lint van Excel naar het tabblad Invoegen . Klik in de groep Afbeeldingen op Scatter invoegen (X, Y) en klik op de eerste optie met de naam Scatter . Dit levert automatisch de volgende puntenwolk op:

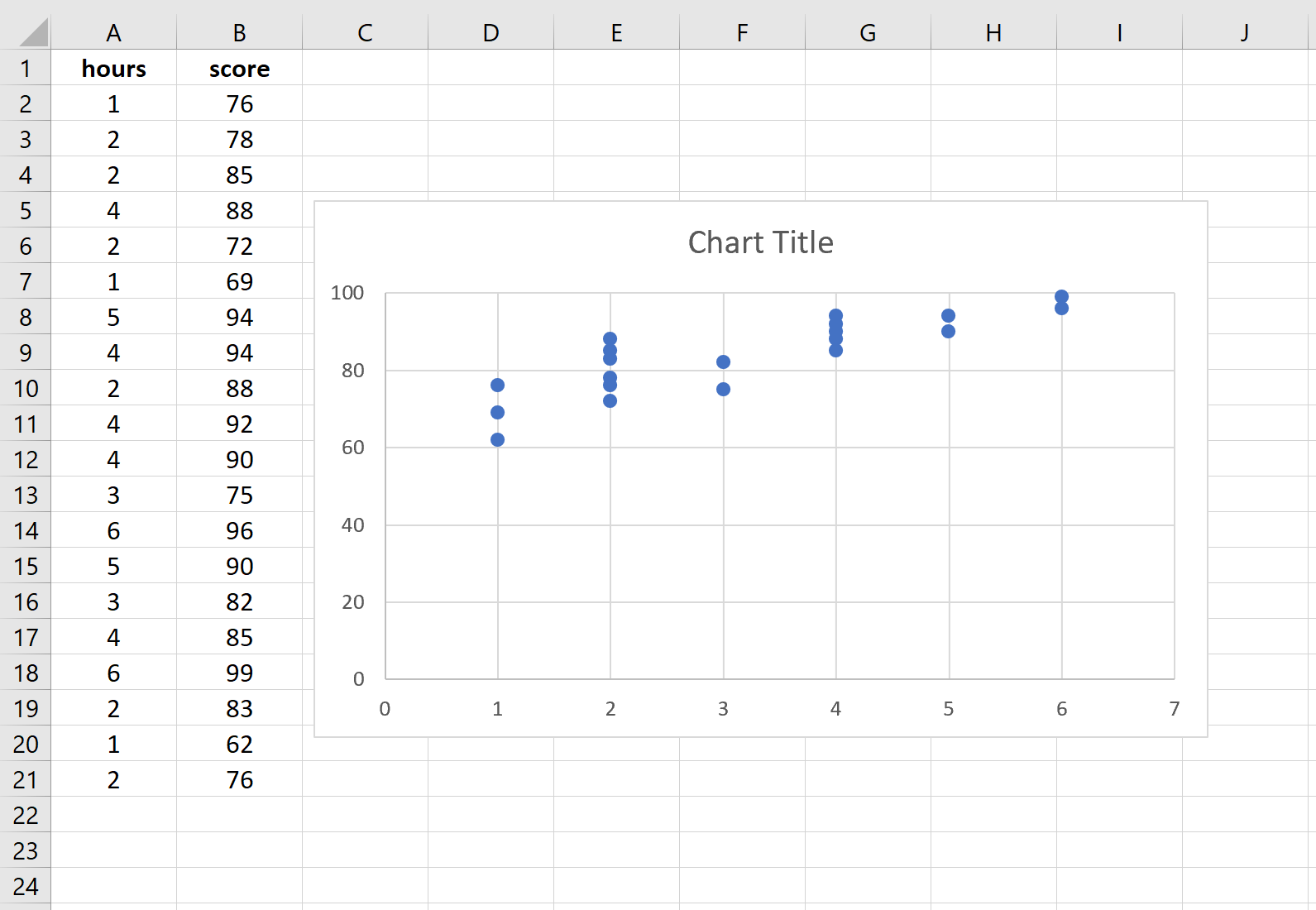
Op de x-as wordt het aantal bestudeerde uren weergegeven en op de y-as de examenresultaten. We zien dat er een lineair verband bestaat tussen de twee variabelen: meer uren studie gaan gepaard met hogere examenscores.

Om de relatie tussen deze twee variabelen te kwantificeren, kunnen we een eenvoudige lineaire regressie uitvoeren.

Stap 3: Voer een eenvoudige lineaire regressie uit.

Ga op het bovenste lint van Excel naar het tabblad Gegevens en klik op Gegevensanalyse . Als u deze optie niet ziet, moet u eerst de gratis Analysis ToolPak-software installeren .

Zodra u op Data-analyse klikt, verschijnt een nieuw venster. Selecteer Regressie en klik op OK.

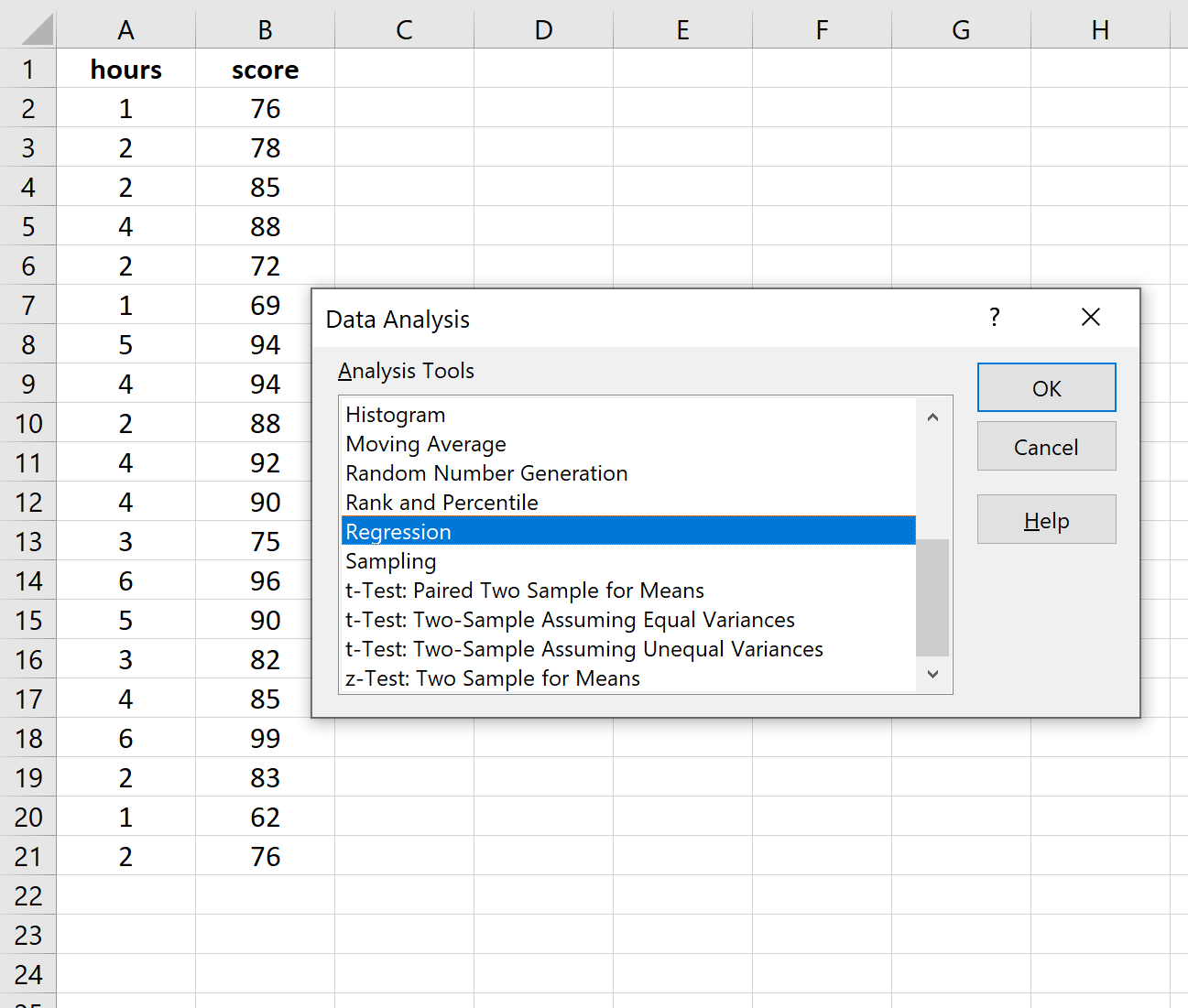
Vul bij Invoer Y- bereik de reeks waarden voor de responsvariabele in. Vul bij Invoer X- bereik de reeks waarden voor de verklarende variabele in.

Vink het vakje naast Labels aan om Excel te laten weten dat we de namen van de variabelen in het invoerbereik hebben opgenomen.

Selecteer bij Uitvoerbereik een cel waarin u de regressie-uitvoer wilt laten verschijnen.

Klik vervolgens op OK .

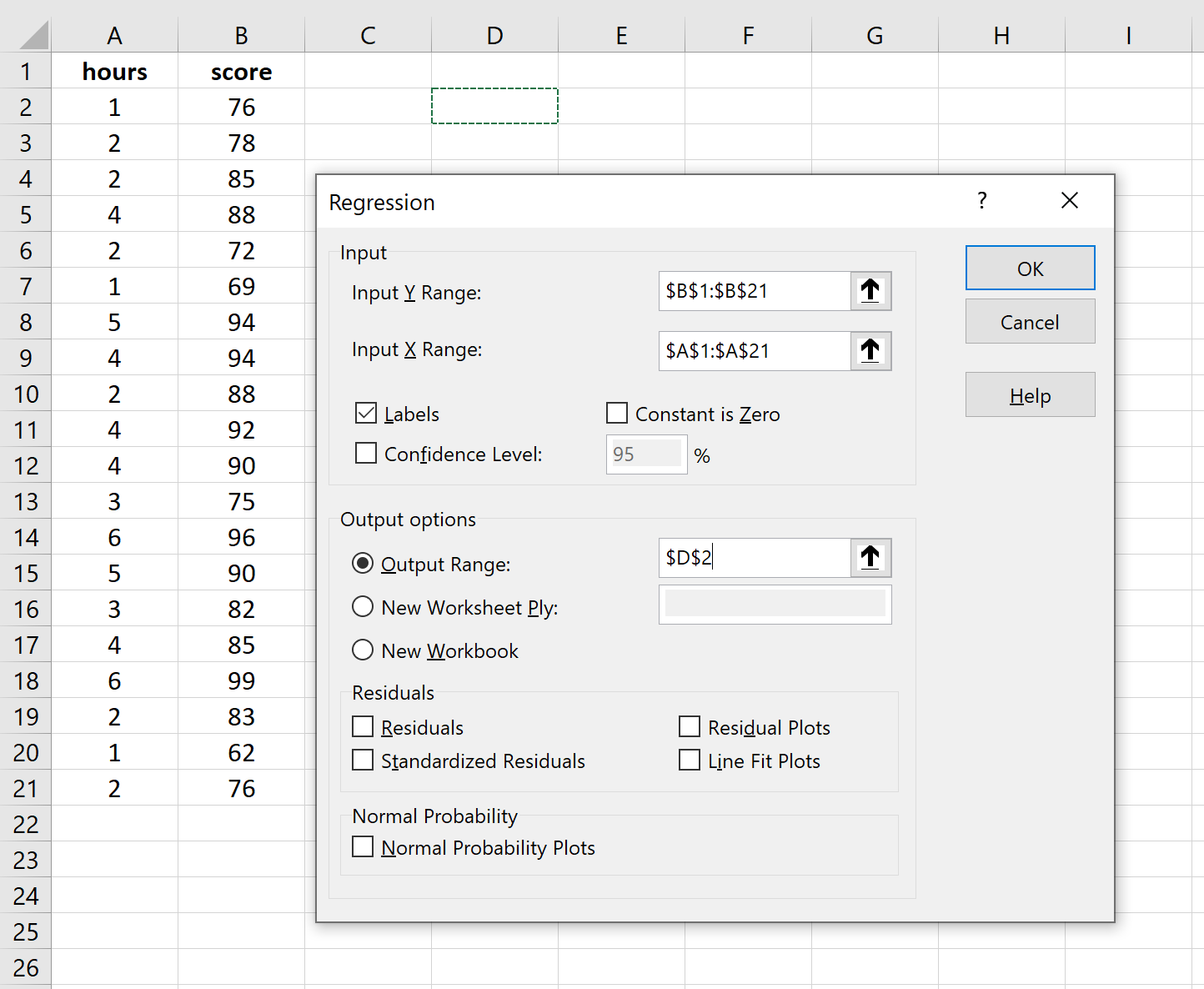
De volgende uitvoer verschijnt automatisch:

Stap 4: Interpreteer het resultaat.

Zo interpreteert u de meest relevante cijfers in het resultaat:

R-kwadraat: 0,7273 . Dit wordt de determinatiecoëfficiënt genoemd. Het is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld wordt 72,73% van de variatie in examenscores verklaard door het aantal gestudeerde uren.

Standaardfout: 5.2805 . Dit is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 5,2805 eenheden af van de regressielijn.

V: 47,9952 . Dit is de algemene F-statistiek voor het regressiemodel, berekend als regressie-MS/residuele MS.

Betekenis F: 0,0000 . Dit is de p-waarde die is gekoppeld aan de algehele F-statistiek. Dit vertelt ons of het regressiemodel statistisch significant is of niet. Met andere woorden, het vertelt ons of de verklarende variabele een statistisch significant verband heeft met de responsvariabele. In dit geval is de p-waarde kleiner dan 0,05, wat aangeeft dat er een statistisch significant verband bestaat tussen het aantal gestudeerde uren en het cijfer dat op het examen wordt behaald.

Coëfficiënten: De coëfficiënten geven ons de getallen die nodig zijn om de geschatte regressievergelijking te schrijven. In dit voorbeeld is de geschatte regressievergelijking:

examenscore = 67,16 + 5,2503*(uren)

We interpreteren de urencoëfficiënt zo dat voor elk extra bestudeerd uur de examenscore gemiddeld met 5,2503 zou moeten stijgen. We interpreteren de coëfficiënt van het intercept zo dat de verwachte examenscore voor een student die nul uur studeert 67,16 is.

Met deze geschatte regressievergelijking kunnen we de verwachte examenscore voor een student berekenen, op basis van het aantal uren studie.

Een student die bijvoorbeeld drie uur studeert, moet een examenscore van 82,91 behalen:

examenscore = 67,16 + 5,2503*(3) = 82,91

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in Excel kunt uitvoeren:

Hoe u een restplot in Excel maakt
Hoe u een voorspellingsinterval in Excel kunt construeren
Hoe u een QQ-plot maakt in Excel