Hoe u eenvoudige lineaire regressie in python uitvoert (stap voor stap)

Eenvoudige lineaire regressie is een techniek die we kunnen gebruiken om de relatie tussen een enkele verklarende variabele en een enkele responsvariabele te begrijpen.

Deze techniek vindt een lijn die het beste bij de gegevens past en neemt de volgende vorm aan:

ŷ = _b0 + _b1 x

Goud:

• ŷ : De geschatte responswaarde
• b ₀ : De oorsprong van de regressielijn
• b ₁ : De helling van de regressielijn

Deze vergelijking kan ons helpen de relatie tussen de verklarende variabele en de responsvariabele te begrijpen en kan (ervan uitgaande dat deze statistisch significant is) worden gebruikt om de waarde van een responsvariabele te voorspellen gegeven de waarde van de verklarende variabele.

Deze tutorial biedt stapsgewijze uitleg over het uitvoeren van eenvoudige lineaire regressie in Python.

Stap 1: Gegevens laden

Voor dit voorbeeld maken we een nep-dataset met de volgende twee variabelen voor 15 studenten:

• Totaal aantal uren gestudeerd voor bepaalde examens
• Examenresultaat

We zullen proberen een eenvoudig lineair regressiemodel in te passen met uren als verklarende variabele en onderzoeksresultaten als responsvariabele.

De volgende code laat zien hoe u deze nep-dataset in Python kunt maken:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

Stap 2: Visualiseer de gegevens

Voordat we een eenvoudig lineair regressiemodel kunnen toepassen, moeten we eerst de gegevens visualiseren om deze te begrijpen.

Ten eerste willen we ervoor zorgen dat de relatie tussen uren en score ongeveer lineair is, aangezien dit een onderliggende aanname is van eenvoudige lineaire regressie.

We kunnen een eenvoudig spreidingsdiagram maken om de relatie tussen de twee variabelen te visualiseren:

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

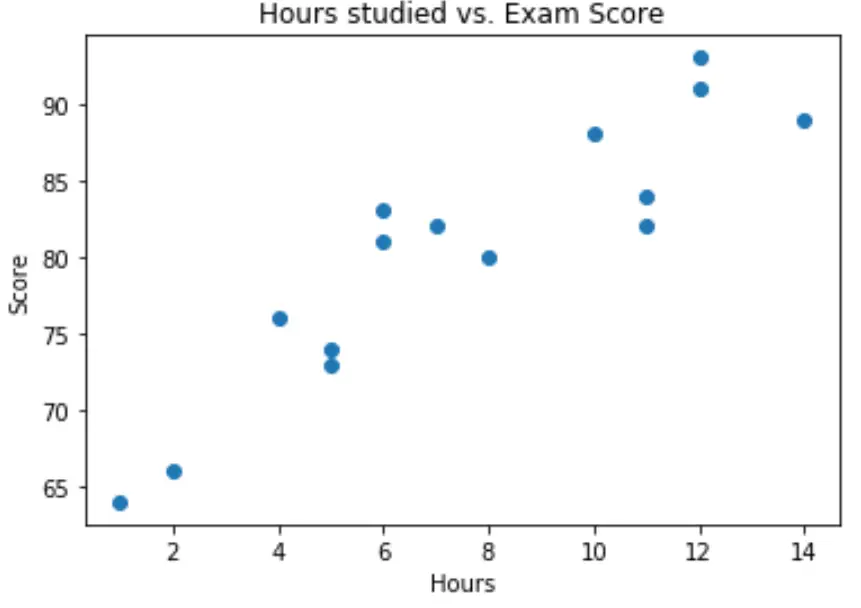
Uit de grafiek kunnen we zien dat de relatie lineair lijkt te zijn. Naarmate het aantal uren toeneemt, stijgt de score ook lineair.

Vervolgens kunnen we een boxplot maken om de verdeling van de examenresultaten te visualiseren en te controleren op uitschieters . Standaard definieert Python een waarneming als een uitbijter als deze 1,5 keer de interkwartielafstand boven het derde kwartiel (Q3) of 1,5 keer de interkwartielafstand onder het eerste kwartiel (Q1) ligt.

Als een waarneming een uitbijter is, verschijnt er een kleine cirkel in de boxplot:

 df. boxplot (column=[' score ']) 

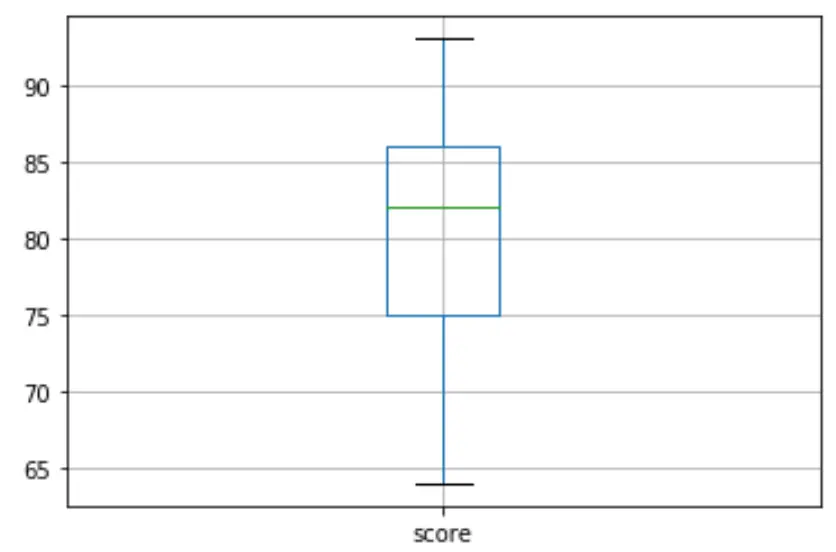
Er zijn geen kleine cirkels in de boxplot, wat betekent dat er geen uitschieters in onze dataset voorkomen.

Stap 3: Voer een eenvoudige lineaire regressie uit

Zodra we hebben bevestigd dat de relatie tussen onze variabelen lineair is en er geen uitschieters zijn, kunnen we overgaan tot het fitten van een eenvoudig lineair regressiemodel met uren als verklarende variabele en de score als responsvariabele:

Opmerking: we zullen de functie OLS() uit de statsmodels-bibliotheek gebruiken om in het regressiemodel te passen.

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Uit de samenvatting van het model kunnen we zien dat de aangepaste regressievergelijking is:

Score = 65.334 + 1.9824*(uren)

Dit betekent dat elk extra bestudeerd uur gepaard gaat met een gemiddelde stijging van de examenscore van 1,9824 punten. En de oorspronkelijke waarde van 65.334 vertelt ons de gemiddelde verwachte examenscore voor een student die nul uur studeert.

We kunnen deze vergelijking ook gebruiken om de verwachte examenscore te vinden op basis van het aantal uren dat een student studeert. Een student die bijvoorbeeld 10 uur studeert, moet een examenscore van 85,158 behalen:

Score = 65,334 + 1,9824*(10) = 85,158

Zo interpreteert u de rest van de modelsamenvatting:

• P>|t| : Dit is de p-waarde die is gekoppeld aan de modelcoëfficiënten. Omdat de p-waarde voor uren (0,000) aanzienlijk kleiner is dan 0,05, kunnen we zeggen dat er een statistisch significant verband bestaat tussen uren en score .
• R-kwadraat: Dit getal vertelt ons dat het percentage variatie in examenscores kan worden verklaard door het aantal gestudeerde uren. Over het algemeen geldt dat hoe groter de R-kwadraatwaarde van een regressiemodel is, hoe beter de verklarende variabelen de waarde van de responsvariabele kunnen voorspellen. In dit geval wordt 83,1% van de variatie in scores verklaard door bestudeerde uren.
• F-statistiek en p-waarde: De F-statistiek ( 63.91 ) en de bijbehorende p-waarde ( 2.25e-06 ) vertellen ons de algehele betekenis van het regressiemodel, dat wil zeggen of de verklarende variabelen in het model nuttig zijn bij het verklaren van variatie . in de responsvariabele. Omdat de p-waarde in dit voorbeeld kleiner is dan 0,05, is ons model statistisch significant en worden uren als nuttig beschouwd bij het verklaren van de scorevariatie .

Stap 4: Maak resterende plots

Nadat het eenvoudige lineaire regressiemodel aan de gegevens is aangepast, is de laatste stap het maken van residuele plots.

Een van de belangrijkste aannames van lineaire regressie is dat de residuen van een regressiemodel bij benadering normaal verdeeld zijn en homoscedastisch zijn op elk niveau van de verklarende variabele. Als niet aan deze aannames wordt voldaan, kunnen de resultaten van ons regressiemodel misleidend of onbetrouwbaar zijn.

Om te verifiëren dat aan deze aannames wordt voldaan, kunnen we de volgende restplots maken:

Plot van residuen versus aangepaste waarden: deze plot is nuttig voor het bevestigen van homoscedasticiteit. Op de x-as worden de gefitte waarden weergegeven en op de y-as de residuen. Zolang de residuen willekeurig en uniform verspreid lijken te zijn over de grafiek rond de nulwaarde, kunnen we aannemen dat de homoscedasticiteit niet wordt geschonden:

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

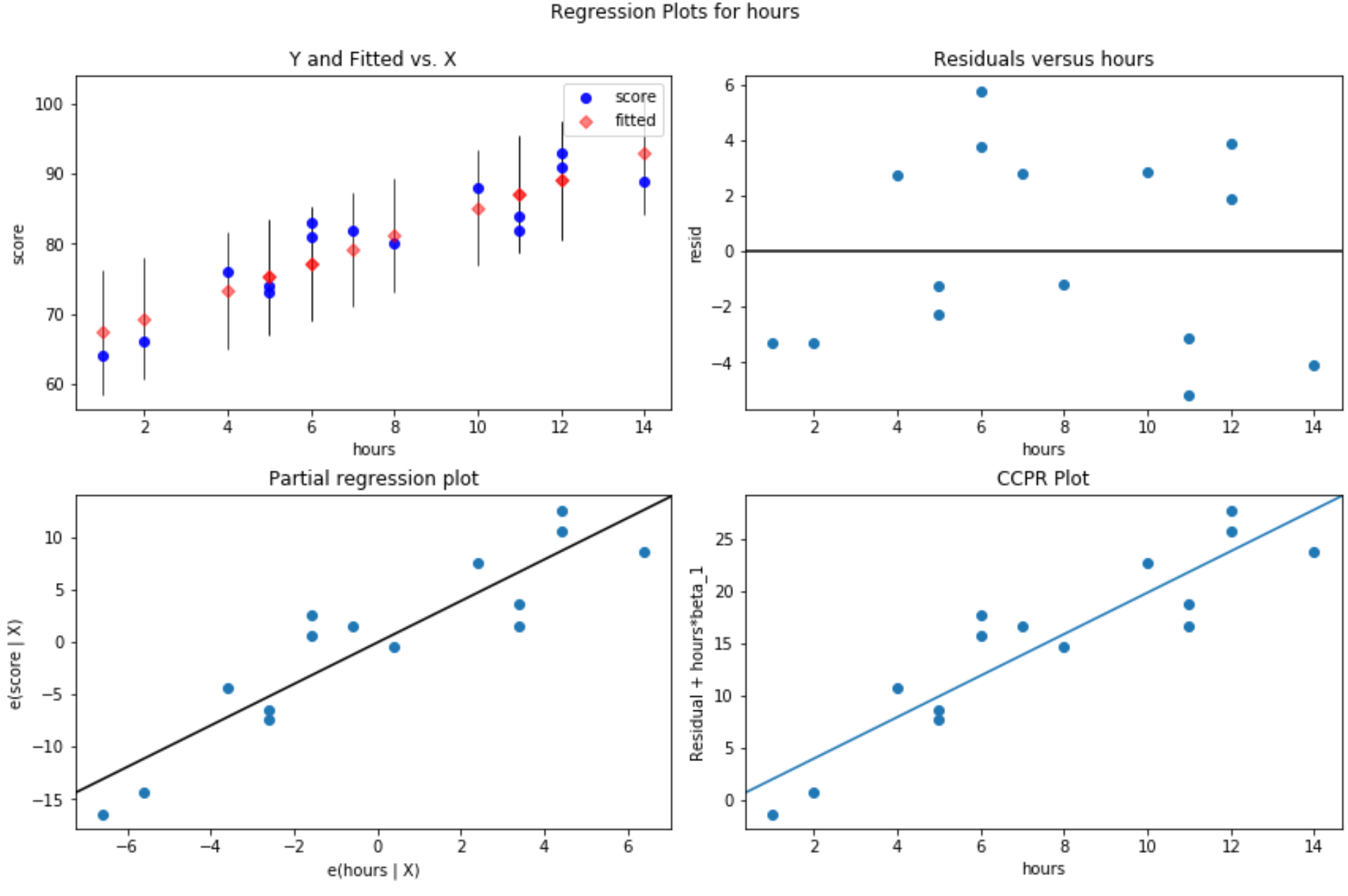
Er worden vier plots geproduceerd. De grafiek in de rechterbovenhoek is de restgrafiek versus de aangepaste grafiek. De x-as in deze grafiek toont de werkelijke waarden van de punten van de voorspellende variabele en de y-as toont het residu voor die waarde.

Omdat de residuen willekeurig rond nul verspreid lijken te zijn, geeft dit aan dat heteroscedasticiteit geen probleem is met de verklarende variabele.

QQ-plot: Deze plot is nuttig om te bepalen of de residuen een normale verdeling volgen. Als de gegevenswaarden in de grafiek een ruwweg rechte lijn volgen in een hoek van 45 graden, zijn de gegevens normaal verdeeld:

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

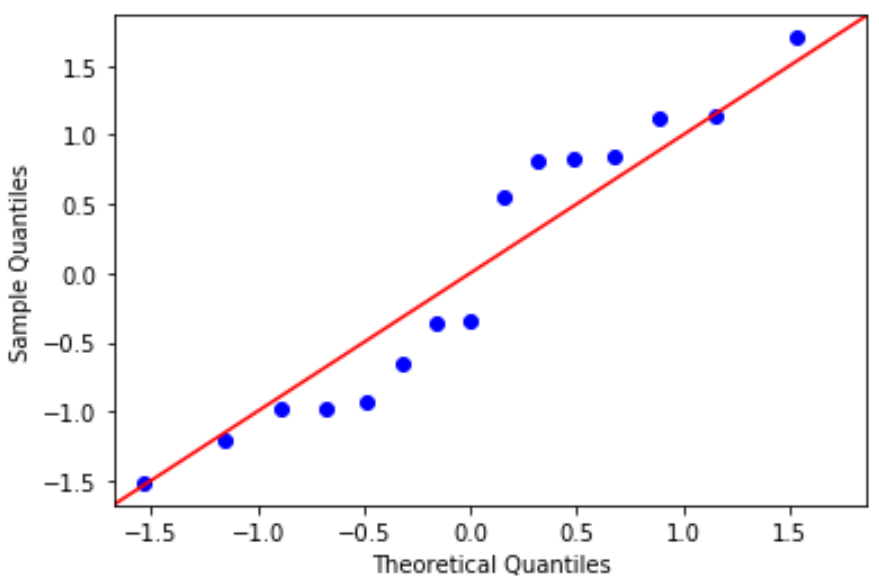
De residuen wijken een beetje af van de 45 graden-lijn, maar niet genoeg om ernstige zorgen te veroorzaken. We kunnen ervan uitgaan dat aan de normaliteitsaanname is voldaan.

Omdat de residuen normaal verdeeld en homoscedastisch zijn, hebben we geverifieerd dat aan de aannames van het eenvoudige lineaire regressiemodel is voldaan. De output van ons model is dus betrouwbaar.

De volledige Python-code die in deze tutorial wordt gebruikt, kun je hier vinden.