Hoe eenvoudige lineaire regressie uit te voeren in stata

Eenvoudige lineaire regressie is een methode die u kunt gebruiken om de relatie tussen een verklarende variabele, x, en een responsvariabele, y, te begrijpen.

In deze tutorial wordt uitgelegd hoe u een eenvoudige lineaire regressie uitvoert in Stata.

Voorbeeld: eenvoudige lineaire regressie in Stata

Stel dat we de relatie willen begrijpen tussen het gewicht van een auto en het aantal kilometers per gallon. Om deze relatie te onderzoeken, kunnen we een eenvoudige lineaire regressie uitvoeren met gewicht als verklarende variabele en mijlen per gallon als responsvariabele.

Voer de volgende stappen in Stata uit om een eenvoudige lineaire regressie uit te voeren met behulp van de dataset genaamd auto , die gegevens over 74 verschillende auto’s bevat.

Stap 1: Gegevens laden.

Laad de gegevens door het volgende in het opdrachtvenster te typen:

gebruik https://www.stata-press.com/data/r13/auto

Stap 2: Krijg een gegevensoverzicht.

Krijg snel inzicht in de gegevens waarmee u werkt door het volgende in het opdrachtvak te typen:

samenvatten

We kunnen zien dat er twaalf verschillende variabelen in de dataset zitten, maar de enige twee waar we om geven zijn mpg enweight .

Stap 3: Visualiseer de gegevens.

Voordat we een eenvoudige lineaire regressie uitvoeren, maken we eerst een spreidingsdiagram van gewicht versus mpg, zodat we de relatie tussen deze twee variabelen kunnen visualiseren en kunnen controleren op duidelijke uitschieters. Typ het volgende in het vak Opdracht om een spreidingsdiagram te maken:

mpg-gewichtsspreiding

Dit levert het volgende spreidingsdiagram op:

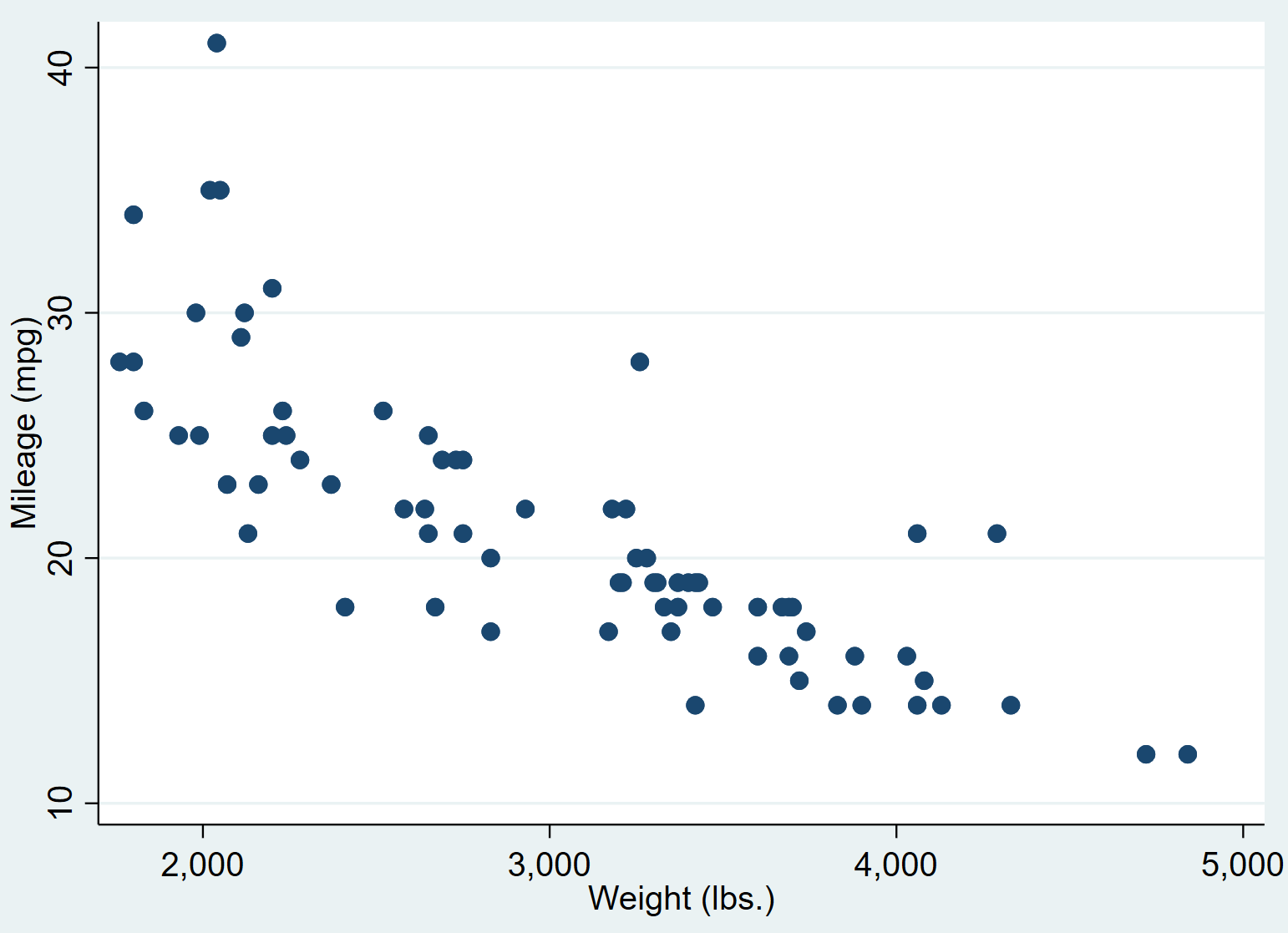
We kunnen zien dat auto’s met hogere gewichten doorgaans minder kilometers per gallon afleggen. Om deze relatie te kwantificeren, zullen we nu een eenvoudige lineaire regressie uitvoeren.

Stap 4: Voer een eenvoudige lineaire regressie uit.

Typ het volgende in het vak Opdracht om een eenvoudige lineaire regressie uit te voeren, waarbij u gewicht als verklarende variabele en mpg als responsvariabele gebruikt.

gewicht terugbrengen naar mpg

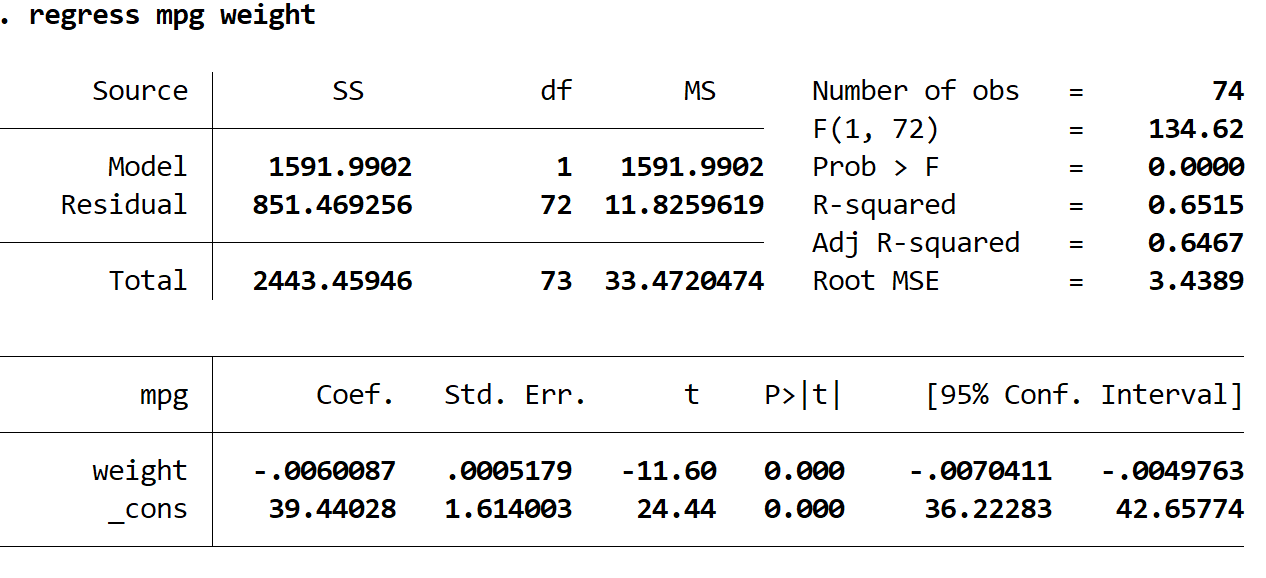
Zo interpreteert u de meest interessante cijfers in het resultaat:

R kwadraat: 0,6515. Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld kan 65,15% van de variatie in mpg worden verklaard aan de hand van het gewicht.

Coef (gewicht): -0,006. Dit vertelt ons de gemiddelde verandering in de responsvariabele die gepaard gaat met een toename van één eenheid in de verklarende variabele. In dit voorbeeld gaat elke gewichtstoename van één pond gepaard met een afname van gemiddeld 0,006 mpg.

Coef (_cons): 39.44028. Dit vertelt ons de gemiddelde waarde van de responsvariabele wanneer de verklarende variabele nul is. In dit voorbeeld is de gemiddelde mpg 39,44028 wanneer het gewicht van een auto nul is. Dit is niet echt logisch om te interpreteren, aangezien het gewicht van een auto niet nul kan zijn, maar het getal 39,44028 is nodig om een regressievergelijking te vormen.

P>|t| (gewicht): 0,000. Dit is de p-waarde die is gekoppeld aan de teststatistiek voor gewicht. In dit geval kunnen we, aangezien deze waarde kleiner is dan 0,05, concluderen dat er een statistisch significante relatie bestaat tussen gewicht en mpg.

Regressievergelijking: Ten slotte kunnen we een regressievergelijking vormen met behulp van de twee coëfficiëntwaarden. In dit geval zou de vergelijking zijn:

voorspelde mpg = 39,44028 – 0,0060087*(gewicht)

We kunnen deze vergelijking gebruiken om het verwachte mpg voor een auto te vinden, gegeven zijn gewicht. Een auto die 4.000 pond weegt, zou bijvoorbeeld een mpg van 15.405 moeten hebben:

voorspelde mpg = 39,44028 – 0,0060087*(4000) = 15,405

Stap 5: Rapporteer de resultaten.

Ten slotte willen we de resultaten van onze eenvoudige lineaire regressie rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een lineaire regressie uitgevoerd om de relatie tussen het gewicht van een auto en het aantal kilometers per gallon te kwantificeren. Voor de analyse is gebruik gemaakt van een steekproef van 74 auto’s.

De resultaten toonden aan dat er een statistisch significante relatie was tussen gewicht en mpg (t = -11,60, p < 0,0001) en dat gewicht verantwoordelijk was voor 65,15% van de verklaarde variabiliteit in mpg.

De regressievergelijking bleek:

voorspelde mpg = 39,44 – 0,006 (gewicht)

Elk extra pond ging gepaard met een afname van gemiddeld -0,006 mijl per gallon.