Hoe de elbow-methode in r te gebruiken om optimale clusters te vinden

Een van de meest gebruikte clusteralgoritmen bij machinaal leren staat bekend als k-means clustering .

K-means clustering is een techniek waarbij we elke waarneming uit een dataset in een van de K- clusters plaatsen.

Het einddoel is om K- clusters te hebben waarin waarnemingen binnen elke cluster behoorlijk op elkaar lijken, terwijl waarnemingen in verschillende clusters behoorlijk van elkaar verschillen.

Bij k-means clustering is de eerste stap het kiezen van een waarde voor K – het aantal clusters waarin we waarnemingen willen plaatsen.

Een van de meest gebruikelijke manieren om een waarde voor K te kiezen staat bekend als de elleboogmethode , waarbij een grafiek wordt gemaakt met het aantal clusters op de x-as en het totaal in de som van de kwadraten op de y-as. waar een „knie“ of draai in de plot verschijnt.

Het punt op de x-as waar de ‘knie’ voorkomt, vertelt ons het optimale aantal clusters dat we kunnen gebruiken in het k-means clusteringalgoritme.

Het volgende voorbeeld laat zien hoe u de elleboogmethode in R gebruikt.

Voorbeeld: gebruik van de elleboogmethode in R

Voor dit voorbeeld gebruiken we de in R ingebouwde USArrests- dataset, die het aantal arrestaties per 100.000 mensen in elke Amerikaanse staat in 1973 bevat voor moord, mishandeling en verkrachting, evenals het percentage van de bevolking van elke staat dat in stedelijke gebieden woont. gebieden. , UrbanPop.

De volgende code laat zien hoe u de gegevensset laadt, rijen met ontbrekende waarden verwijdert en elke variabele in de gegevensset schaalt zodat deze een gemiddelde van 0 en een standaardafwijking van 1 heeft:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Om het optimale aantal clusters te vinden dat we in het k-means-algoritme kunnen gebruiken, zullen we de functie fviz_nblust() uit het factoextra- pakket gebruiken om een grafiek te maken van het aantal clusters versus het totaal in de som van de kwadraten:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

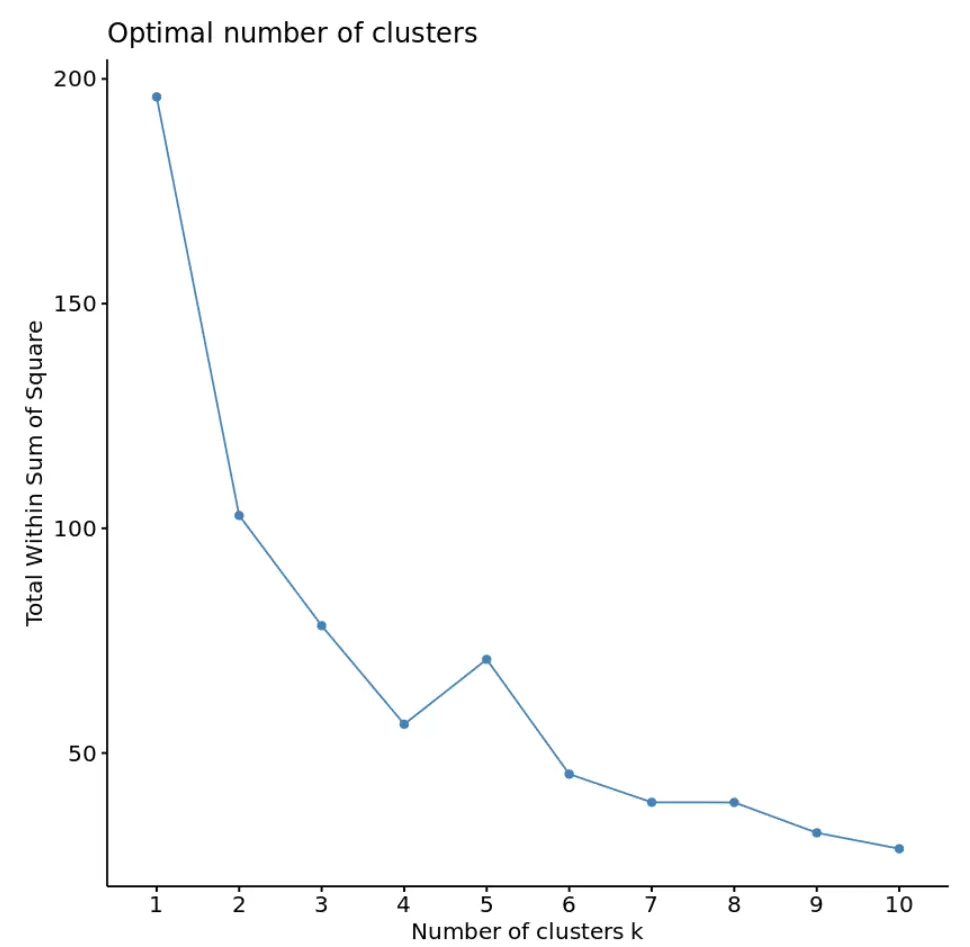
In deze grafiek lijkt het erop dat er een “knie” of knik is bij k = 4 clusters. Dit is het punt waarop het totaal in de som van de kwadraten begint te stabiliseren.

Dit vertelt ons dat het optimale aantal clusters dat in het k-means-algoritme moet worden gebruikt, 4 is.

Opmerking : hoewel we een lager totaal in de som van de kwadraten zouden kunnen krijgen door meer clusters te gebruiken, zouden we waarschijnlijk de trainingsgegevens te veel aanpassen en daarom zou het k-means-algoritme niet zo goed werken op de testgegevens.

We kunnen de kmeans() -functie uit het clusterpakket gebruiken om k-means-clustering op de dataset uit te voeren met behulp van de optimale waarde voor k van 4:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Uit de resultaten kunnen we zien dat:

• Aan het eerste cluster werden 16 staten toegewezen
• Er zijn 13 staten toegewezen aan het tweede cluster
• Er zijn 13 staten toegewezen aan het derde cluster
• Er zijn 8 staten toegewezen aan het vierde cluster

We kunnen ook de clustertoewijzingen van elke staat toevoegen aan de originele dataset:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Elke waarneming uit de oorspronkelijke database werd in een van de vier groepen geplaatst.

Aanvullende bronnen

De volgende zelfstudies bieden stapsgewijze voorbeelden van het uitvoeren van verschillende clusteralgoritmen in R:

K-betekent clustering in R: stapsgewijs voorbeeld
K-Medoids Clustering in R: stapsgewijs voorbeeld
Hiërarchische clustering in R: stapsgewijs voorbeeld