Empirische waarschijnlijkheid

In dit artikel leggen we uit hoe je de empirische waarschijnlijkheid kunt berekenen. Je ontdekt wat empirische waarschijnlijkheid is, wat de formule ervan is, een voorbeeld en wat de verschillen zijn tussen empirische waarschijnlijkheid en theoretische waarschijnlijkheid.

Wat is empirische waarschijnlijkheid?

Empirische waarschijnlijkheid is een statistische maatstaf gebaseerd op empirische experimenten of feiten die de waarschijnlijkheid aangeeft dat een gebeurtenis plaatsvindt.

Met andere woorden: de empirische waarschijnlijkheid wordt berekend op basis van de resultaten van een experiment en vertelt ons hoe waarschijnlijk het is dat een gebeurtenis zal plaatsvinden.

Hoe vaker het experiment wordt herhaald, hoe nauwkeuriger de verkregen empirische waarschijnlijkheid zal zijn. Daarom wordt dit soort waarschijnlijkheid meestal bepaald met behulp van computerprogramma’s die duizenden iteraties simuleren en deze in zeer korte tijd kunnen analyseren.

Empirische waarschijnlijkheid is een getal tussen 0 en 1. Hoe waarschijnlijker het is dat een gebeurtenis zal plaatsvinden, hoe hoger de empirische waarschijnlijkheid, en omgekeerd: hoe kleiner de kans dat een gebeurtenis zal plaatsvinden, hoe lager de empirische waarschijnlijkheid ervan.

Empirische waarschijnlijkheidsformule

De formule voor empirische waarschijnlijkheid is het aantal keren dat een gebeurtenis plaatsvond tijdens een experiment gedeeld door het totale aantal keren dat het experiment werd uitgevoerd.

Als we bijvoorbeeld tien keer naar een boom kijken en zeven keer een vogel in de boom hebben gezien, is de empirische waarschijnlijkheid dat we een vogel zien terwijl we naar de boom kijken:

Voorbeeld van empirische waarschijnlijkheid

Gezien de definitie van empirische waarschijnlijkheid, zullen we een stapsgewijze oefening met dit soort waarschijnlijkheid oplossen. Zo kun je zien hoe de empirische waarschijnlijkheid wordt berekend.

• Berekent de empirische waarschijnlijkheid van de elementaire gebeurtenissen waaruit het willekeurige experiment van het gooien van een dobbelsteen bestaat.

Eerst zullen we de theoretische waarschijnlijkheid berekenen van het vergelijken van de verkregen experimentele resultaten met de theoretische resultaten. Er zijn zes mogelijke uitkomsten bij het gooien van een dobbelsteen (1, 2, 3, 4, 5 en 6), dus de theoretische waarschijnlijkheid van elke elementaire gebeurtenis is:

Om deze oefening op te lossen, moeten we simuleren dat we meerdere keren met een dobbelsteen gooien en de resultaten in een kruistabel vastleggen. Hiervoor kunnen we bijvoorbeeld het programma Excel gebruiken.

Om het belang van het aantal uitgevoerde experimenten te kunnen zien, zullen we eerst tien lanceringen simuleren, daarna honderd en ten slotte duizend. De resultaten verkregen uit de simulatie van de eerste 10 willekeurige worpen van een dobbelsteen zijn dus als volgt:

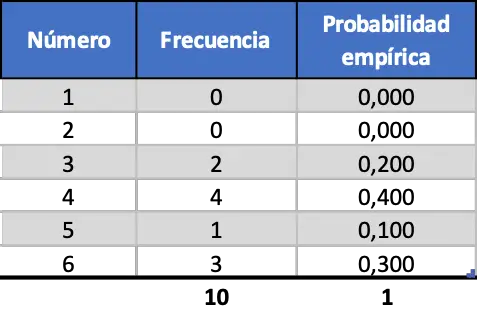
Zoals u kunt zien, komen de empirische kansen die worden verkregen door het simuleren van slechts tien worpen niet in de buurt van de theoretische kansen (0,167).

Maar naarmate we het aantal experimenten vergroten, gaan deze twee statistieken meer op elkaar lijken, kijk eens naar de simulatie van 100 lanceringen:

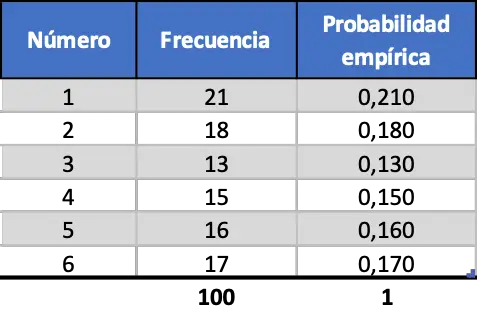
Nu lijkt de empirische waarschijnlijkheid die voor elk getal op de dobbelsteen wordt berekend meer op de theoretische waarschijnlijkheid, maar we krijgen nog steeds heel verschillende waarden.

Ten slotte voeren we dezelfde procedure uit, maar simuleren we 1000 lanceringen:

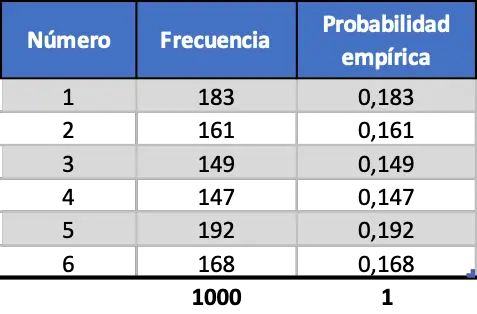
Zoals we in de laatste contingentietabel kunnen zien, liggen de waarden van de empirische waarschijnlijkheden nu heel dicht bij de theoretische waarschijnlijkheden.

Samenvattend : hoe meer we het aantal uitgevoerde experimenten vergroten, hoe dichter de waarde van de empirische waarschijnlijkheid van een gebeurtenis zal liggen bij de theoretische waarschijnlijkheid van optreden . Deze regel wordt gedefinieerd als de wet van de grote getallen , die stelt dat hoe meer gegevens er zijn, hoe dichter de experimentele waarden bij de theoretische waarden zullen liggen.

Als we bovendien de drie frequentietabellen vergelijken, zien we dat de empirische waarschijnlijkheid niet definitief is, maar verandert afhankelijk van het aantal uitgevoerde experimenten. Dat betekent dat je moet weten hoe je de verkregen waarden moet interpreteren.

Empirische waarschijnlijkheid en theoretische waarschijnlijkheid

Ten slotte zullen we het begrip empirische waarschijnlijkheid en dat van theoretische waarschijnlijkheid analyseren, omdat het weliswaar twee soorten waarschijnlijkheden zijn, maar een totaal verschillende betekenis hebben.

Het verschil tussen empirische waarschijnlijkheid en theoretische waarschijnlijkheid (of klassieke waarschijnlijkheid) is dat empirische waarschijnlijkheid wordt berekend op basis van gegevens verzameld uit echte ervaring, terwijl theoretische waarschijnlijkheid wordt berekend rekening houdend met ideale omstandigheden zonder enig experiment uit te voeren.

Dat wil zeggen, om de empirische waarschijnlijkheid te vinden, moet een experiment worden gesimuleerd en moet de berekening worden uitgevoerd op basis van de verkregen resultaten. Maar om de theoretische waarschijnlijkheid te kennen, moet er geen experiment worden uitgevoerd, maar eerder een theoretische berekening.

Bovendien wordt de mate van vertekening gedefinieerd als het verschil tussen de empirische waarschijnlijkheid en de theoretische waarschijnlijkheid. De vertekening kan positief of negatief zijn, maar het is erg moeilijk om deze nul te laten zijn, omdat dat zou betekenen dat een willekeurig experiment precies de theoretische waarschijnlijkheid bereikt, wat zeer onwaarschijnlijk is.