Hoe qq-plots te gebruiken om de normaliteit te controleren

Een QQ-plot, een afkorting van ‘quantile-quantile’, wordt gebruikt om te evalueren of een dataset mogelijk afkomstig is van een theoretische distributie.

In de meeste gevallen wordt dit type plot gebruikt om te bepalen of een dataset al dan niet een normale verdeling volgt.

Als de gegevens normaal verdeeld zijn, liggen de punten op een QQ-plot op een rechte diagonale lijn.

Omgekeerd geldt dat hoe significanter de punten in de grafiek afwijken van een rechte diagonale lijn, hoe kleiner de kans dat de gegevensset een normale verdeling volgt.

De volgende voorbeelden laten zien hoe u QQ-plots in R kunt maken om de normaliteit te controleren.

Voorbeeld 1: QQ-plot voor normale gegevens

De volgende code laat zien hoe u een normaal verdeelde gegevensset met 200 waarnemingen genereert en een QQ-plot voor de gegevensset in R maakt:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create QQ plot
qqnorm(data)
qqline(data)

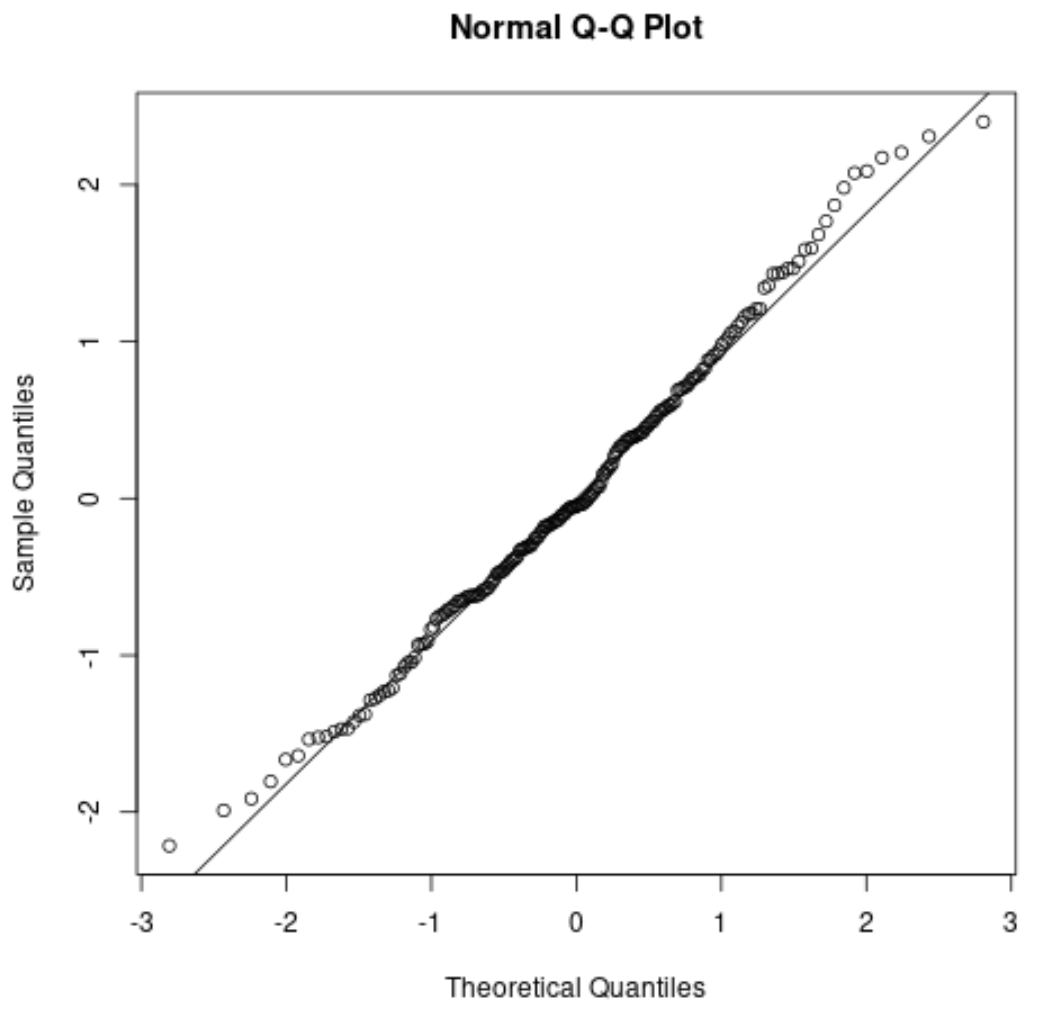
We kunnen zien dat de punten voornamelijk langs de rechte diagonale lijn liggen, met enkele kleine afwijkingen langs elk van de staarten.

Op basis van deze grafiek kunnen we veilig aannemen dat deze dataset normaal verdeeld is.

Voorbeeld 2: QQ-plot voor niet-normale gegevens

De volgende code laat zien hoe u een QQ-plot maakt voor een gegevensset die een exponentiële verdeling volgt met 200 waarnemingen:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create QQ plot
qqnorm(data)
qqline(data)

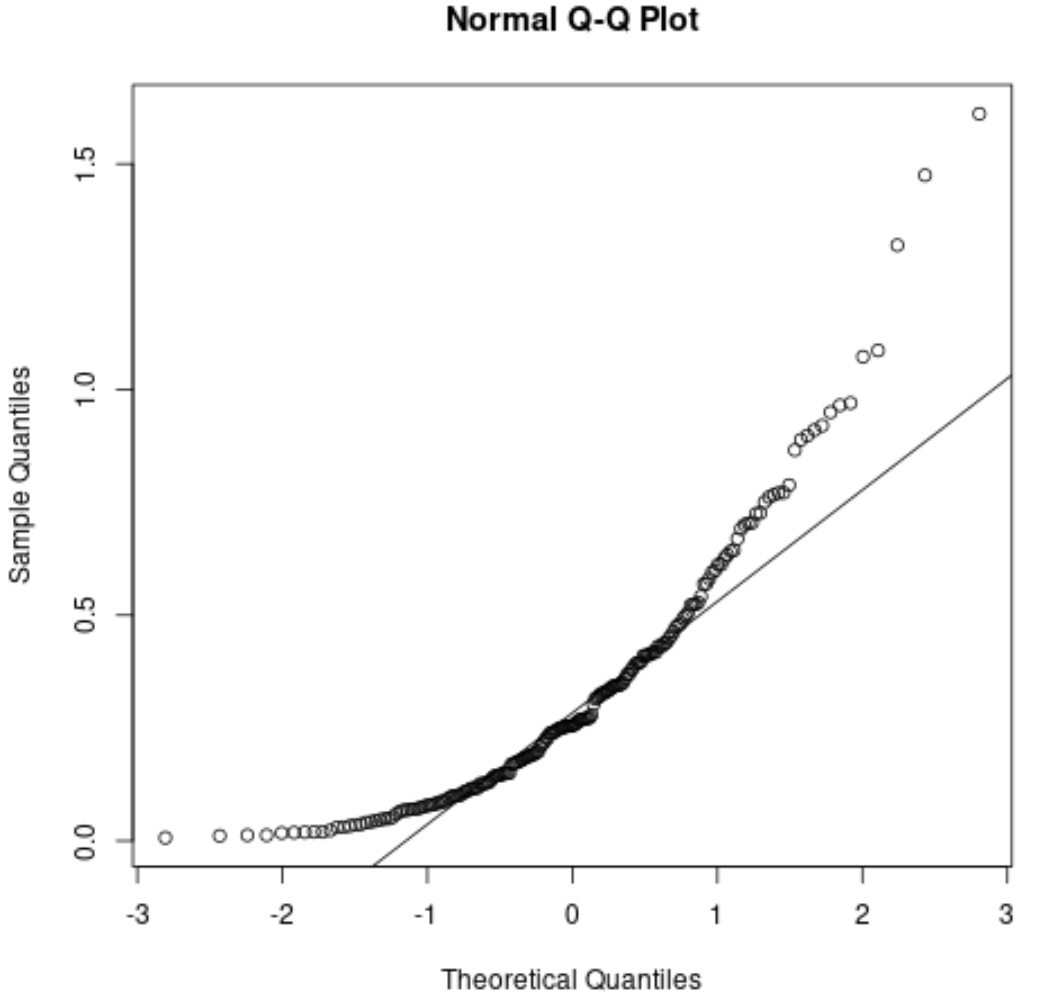
We zien dat de punten flink afwijken van de diagonale lijn. Dit geeft duidelijk aan dat de dataset niet normaal verdeeld is.

Dit zou logisch moeten zijn, aangezien we hebben gespecificeerd dat de gegevens een exponentiële verdeling moeten volgen.

QQ-plots en histogrammen

Opgemerkt moet worden dat QQ-plots een manier zijn om visueel te controleren of een dataset al dan niet een normale verdeling volgt.

Een andere manier om de normaliteit visueel te controleren, is door een histogram van de gegevensset te maken. Als de gegevens in het histogram ongeveer de vorm van een belcurve volgen, kunnen we aannemen dat de gegevensset normaal verdeeld is.

Zo kunt u bijvoorbeeld als volgt een histogram maken voor de eerder normaal verdeelde gegevensset:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create a histogram to visualize the distribution
hist(data) 

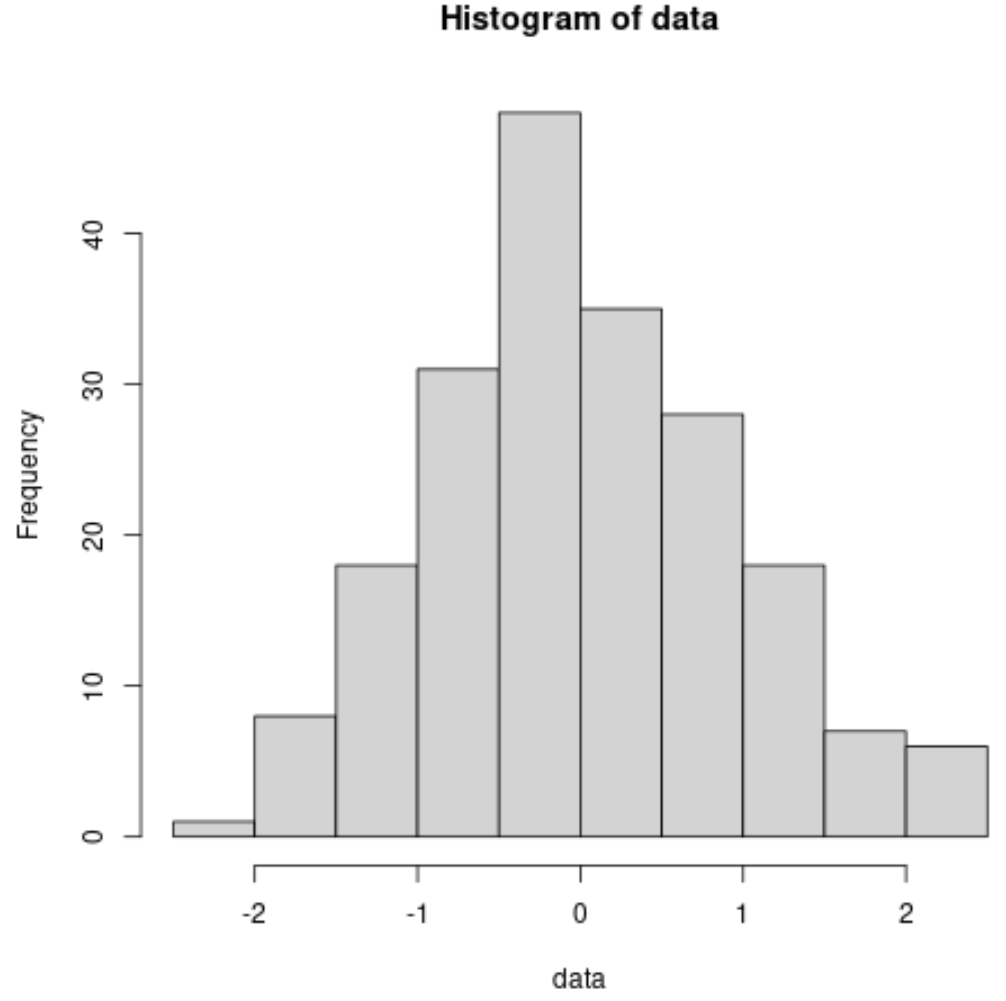
En zo kunt u een histogram maken voor de dataset die een exponentiële eerdere verdeling volgt:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create a histogram to visualize the distribution
hist(data) 

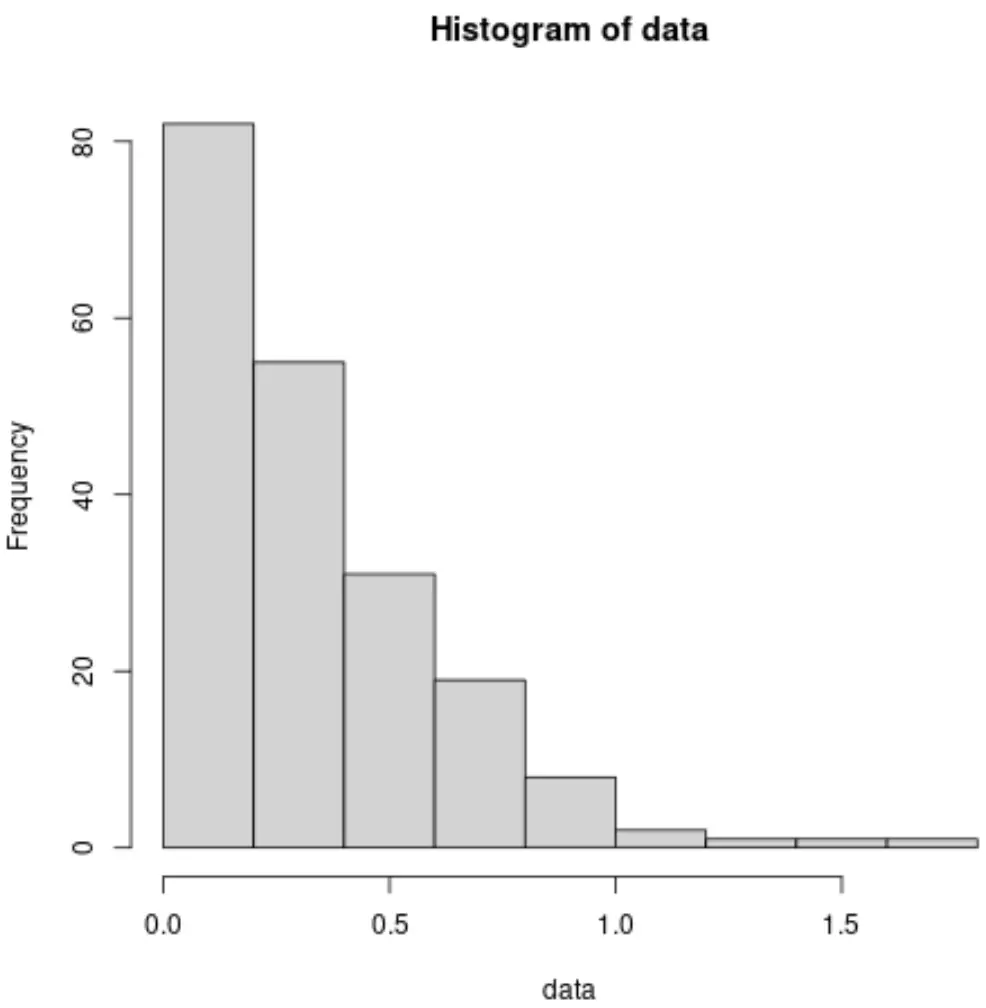
We zien dat het histogram helemaal niet op een belcurve lijkt, wat duidelijk aangeeft dat de gegevens geen normale verdeling volgen.

Aanvullende bronnen

Wat is de normaliteitsaanname in de statistiek?
Hoe maak je een QQ-plot in R
Hoe u een QQ-plot maakt in Excel
Hoe u een QQ-plot maakt in Python