One-way anova: definitie, formule en voorbeeld
Een one-way ANOVA (“variantieanalyse”) vergelijkt de gemiddelden van drie of meer onafhankelijke groepen om te bepalen of er een statistisch significant verschil bestaat tussen de gemiddelden van de overeenkomstige populatie.
In deze zelfstudie wordt het volgende uitgelegd:
- De motivatie om een one-way ANOVA uit te voeren.
- De aannames waaraan moet worden voldaan om een eenrichtings-ANOVA uit te voeren.
- Het proces voor het uitvoeren van een eenrichtings-ANOVA.
- Een voorbeeld van hoe u een eenrichtings-ANOVA uitvoert.
One-way ANOVA: motivatie
Stel dat we willen weten of drie verschillende examenvoorbereidingsprogramma’s al dan niet tot verschillende gemiddelde scores op een toelatingsexamen voor een universiteit leiden. Aangezien er in het hele land miljoenen middelbare scholieren zijn, zou het te tijdrovend en te duur zijn om naar elke leerling toe te gaan en hem een van de examenvoorbereidingsprogramma’s te laten gebruiken.
In plaats daarvan zouden we drie willekeurige steekproeven van honderd studenten uit de populatie kunnen selecteren en elke steekproef een van de drie toetsvoorbereidingsprogramma’s kunnen laten gebruiken ter voorbereiding op het examen. Dan kunnen we de scores van elke student registreren zodra hij of zij het examen aflegt.
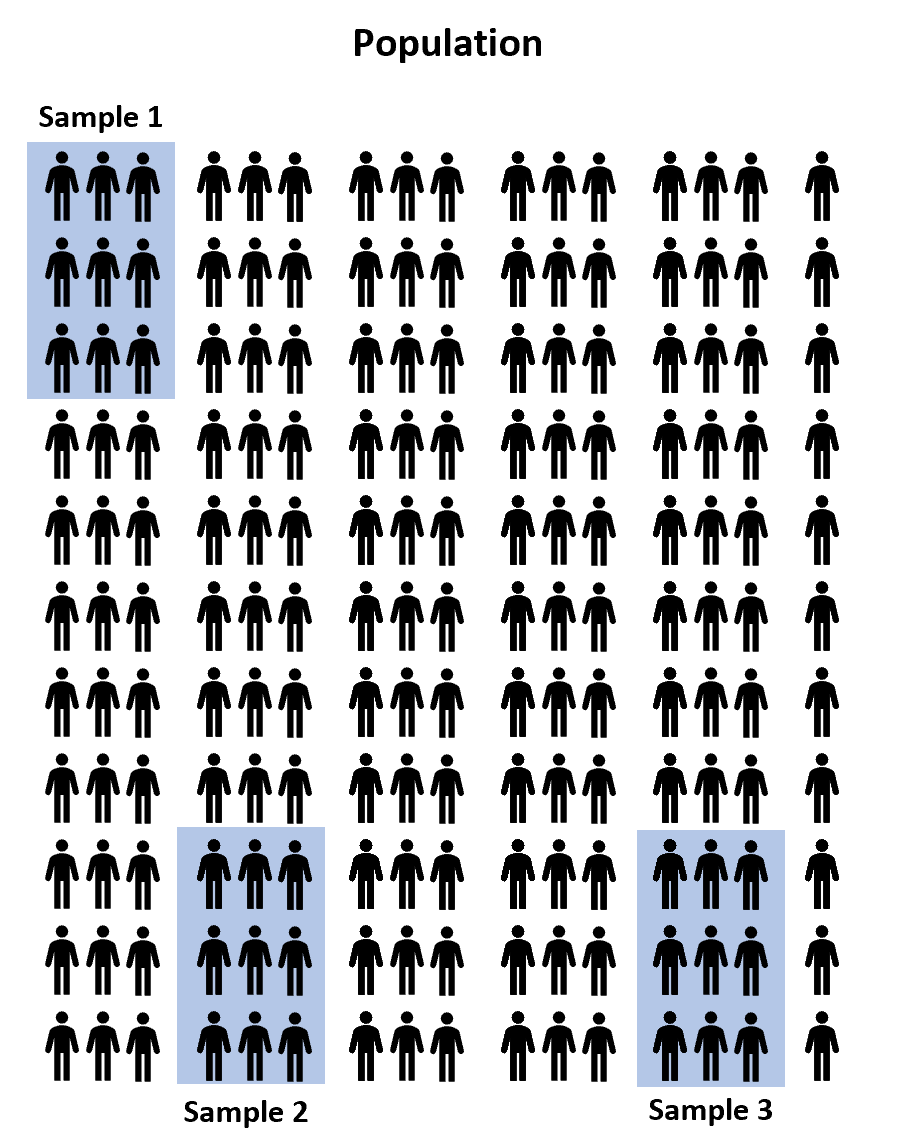
Het is echter vrijwel gegarandeerd dat de gemiddelde examenscore tussen de drie monsters op zijn minst een beetje zal verschillen. De vraag is of dit verschil statistisch significant is . Gelukkig stelt een one-way ANOVA ons in staat deze vraag te beantwoorden.
One-way ANOVA: aannames
Om de resultaten van een eenrichtings-ANOVA geldig te laten zijn, moet aan de volgende aannames worden voldaan:
1. Normaliteit – Elke steekproef werd getrokken uit een normaal verdeelde populatie.
2. Gelijke varianties – De varianties van de populaties waaruit de steekproeven zijn getrokken, zijn gelijk. Je kunt de test van Bartlett gebruiken om deze hypothese te testen.
3. Onafhankelijkheid – De waarnemingen binnen elke groep zijn onafhankelijk van elkaar en de waarnemingen binnen de groepen zijn verkregen door middel van willekeurige steekproeven.
Lees dit artikel voor meer informatie over hoe u deze aannames kunt verifiëren.
One-way ANOVA: het proces
Een eenrichtings-ANOVA gebruikt de volgende nul- en alternatieve hypothesen:
- H 0 (nulhypothese): μ 1 = μ 2 = μ 3 = … = μ k (alle populatiegemiddelden zijn gelijk)
- H 1 (alternatieve hypothese): minstens één populatiegemiddelde is anders rest
Normaal gesproken gebruikt u bepaalde statistische software (zoals R, Excel, Stata, SPSS, enz.) om eenrichtings-ANOVA uit te voeren, omdat dit vervelend is om handmatig uit te voeren.
Ongeacht de software die u gebruikt, ontvangt u de volgende tabel als uitvoer:
| Bron | Som van kwadraten (SS) | df | Gemiddelde kwadraten (MS) | F | P |
|---|---|---|---|---|---|
| Behandeling | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Fout | ESS | df e | MSE | ||
| Totaal | OHS | df t |
Goud:
- SSR: regressie van de kwadratensom
- SSE: som van de gekwadrateerde fout
- SST: totale som van kwadraten (SST = SSR + SSE)
- df r : regressievrijheidsgraden (df r = k-1)
- df e : foutvrijheidsgraden (df e = nk)
- df t : totale vrijheidsgraden (df t = n-1)
- k: totaal aantal groepen
- n: totaal aantal waarnemingen
- MSR: gemiddelde kwadratische regressie (MSR = SSR/df r )
- MSE: gemiddelde kwadratische fout (MSE = SSE/df e )
- F: De F-teststatistiek (F = MSR/MSE)
- p: De waarde p die overeenkomt met F dfr, dfe
Als de p-waarde kleiner is dan het gekozen significantieniveau (bijvoorbeeld 0,05), dan kun je de nulhypothese verwerpen en concluderen dat ten minste één van de populatiegemiddelden verschilt van de andere.
Opmerking: als u de nulhypothese verwerpt, geeft dit aan dat ten minste één van de populatiegemiddelden verschilt van de andere, maar de ANOVA-tabel specificeert niet welke populatiegemiddelden verschillend zijn. Om dit te bepalen, moet u post-hoc-testen uitvoeren, ook wel ‚multiple-vergelijking‘-testen genoemd.
One-way ANOVA: voorbeeld
Stel dat we willen weten of drie verschillende toetsvoorbereidingsprogramma’s al dan niet tot verschillende gemiddelde scores op een bepaald examen leiden. Om dit te testen werven we 30 studenten om mee te doen aan een onderzoek en verdelen ze in drie groepen.
Studenten in elke groep worden willekeurig toegewezen om de komende drie weken een van de drie toetsvoorbereidingsprogramma’s te gebruiken ter voorbereiding op een examen. Aan het einde van de drie weken leggen alle studenten hetzelfde examen af.
Hieronder vindt u de examenresultaten per groep:

Om een one-way ANOVA op deze gegevens uit te voeren, gebruiken we de Statistics One-Way ANOVA Calculator met de volgende invoer:

Uit de uitvoertabel zien we dat de F-teststatistiek 2,358 is en de overeenkomstige p-waarde 0,11385 .

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.
Dit betekent dat we onvoldoende bewijs hebben om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde examenscores van de drie groepen.
Aanvullende bronnen
In de volgende artikelen wordt uitgelegd hoe u een eenrichtings-ANOVA uitvoert met behulp van verschillende statistische software:
Eenrichtings-ANOVA uitvoeren in Excel
Eenrichtings-ANOVA uitvoeren in R
Eenrichtings-ANOVA uitvoeren in Python
Eenrichtings-ANOVA uitvoeren in SAS
Eenrichtings-ANOVA uitvoeren in SPSS
Hoe u eenrichtings-ANOVA uitvoert in Stata
Eenrichtings-ANOVA uitvoeren op een TI-84-rekenmachine
Online One-Way ANOVA-calculator