Eenrichtings-anova uitvoeren in spss

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Dit type test wordt eenrichtings-ANOVA genoemd omdat we de impact van een voorspellende variabele op een responsvariabele analyseren.

Als we in plaats daarvan geïnteresseerd zouden zijn in de impact van twee voorspellende variabelen op een responsvariabele, zouden we een tweerichtings-ANOVA kunnen uitvoeren.

In deze tutorial wordt uitgelegd hoe u een one-way ANOVA uitvoert in SPSS.

Voorbeeld: One-way ANOVA in SPSS

Stel dat een onderzoeker 30 studenten recruteert om aan een onderzoek deel te nemen. Studenten worden willekeurig toegewezen om de volgende maand een van de drie studietechnieken te gebruiken ter voorbereiding op een examen. Aan het einde van de maand maken alle studenten dezelfde toets.

De resultaten van de studententest worden hieronder weergegeven:

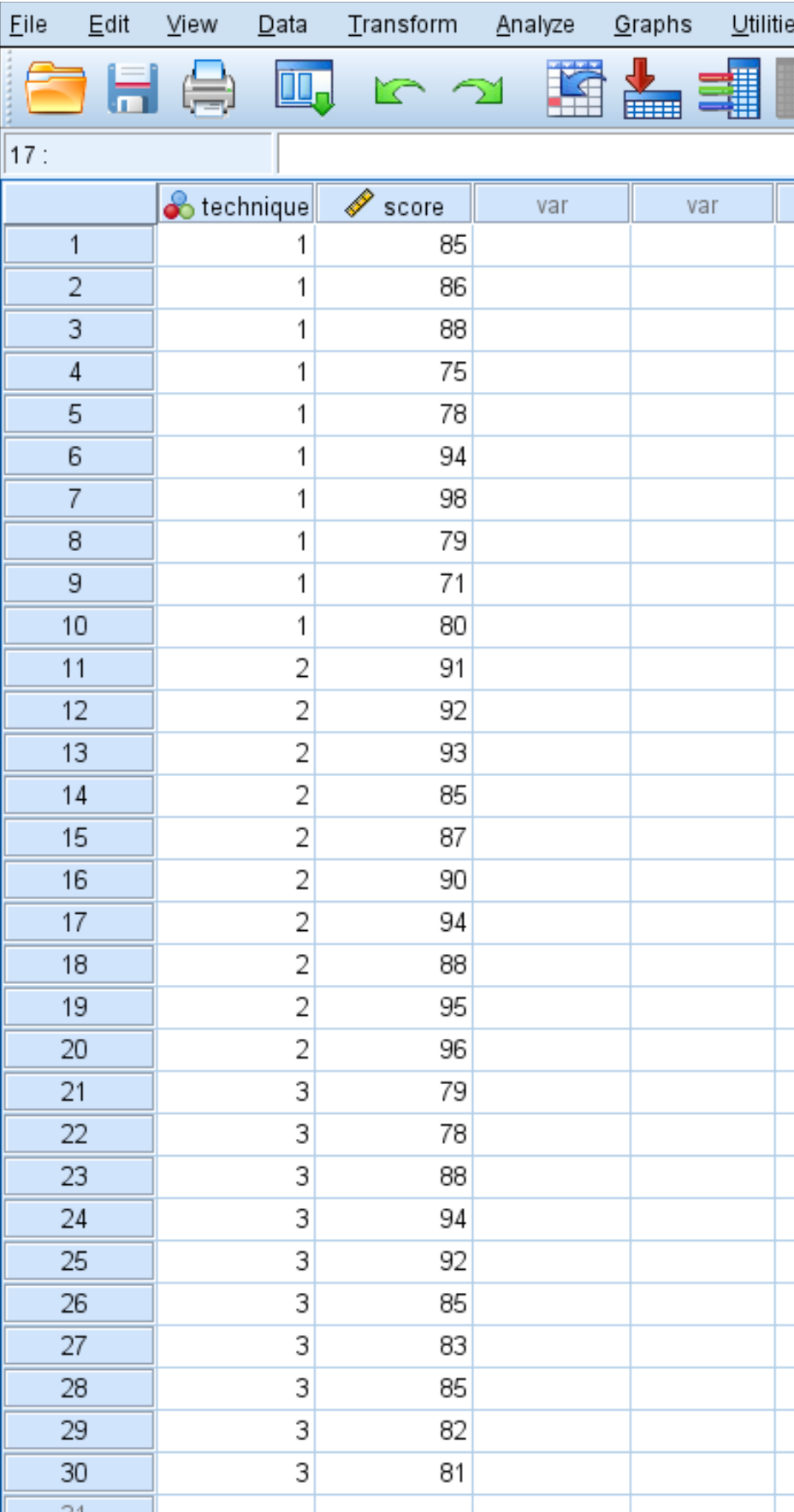
Gebruik de volgende stappen om een eenrichtings-ANOVA uit te voeren om te bepalen of de gemiddelde scores voor de drie groepen hetzelfde zijn.

Stap 1: Visualiseer de gegevens.

Eerst zullen we boxplots maken om de verdeling van testscores voor elk van de drie onderzoekstechnieken te visualiseren. Klik op het tabblad Grafieken en klik vervolgens op Grafiekbouwer .

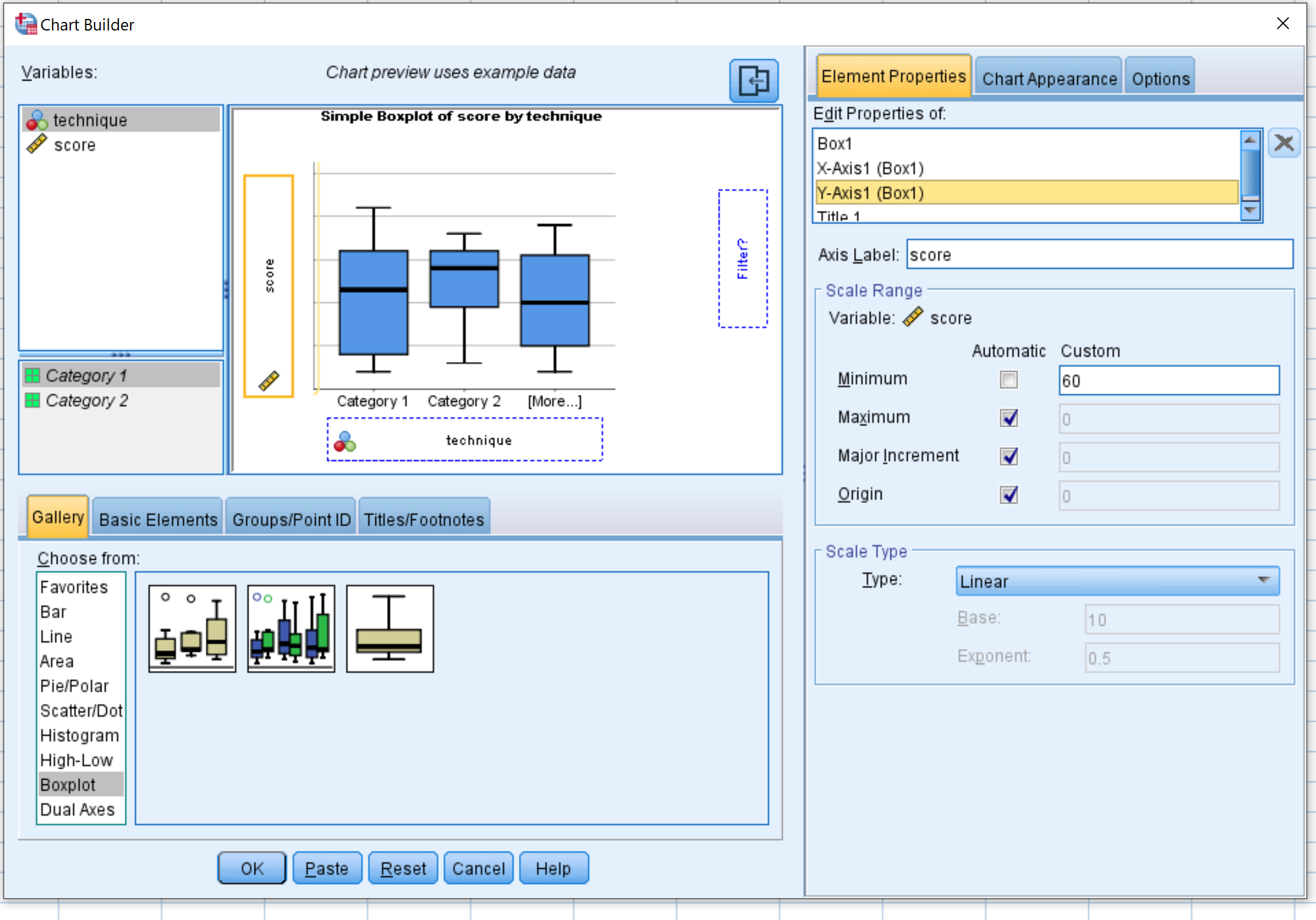
Selecteer Boxplot in het venster Kiezen uit:. Sleep vervolgens het eerste diagram met de naam Simple boxplot naar het hoofdbewerkingsvenster. Sleep de technische variabele op de x-as en de score op de y-as.

Klik vervolgens op Elementeigenschappen en vervolgens op Y1-as . Wijzig de minimumwaarde in 60. Klik vervolgens op OK .

De volgende boxplots verschijnen:

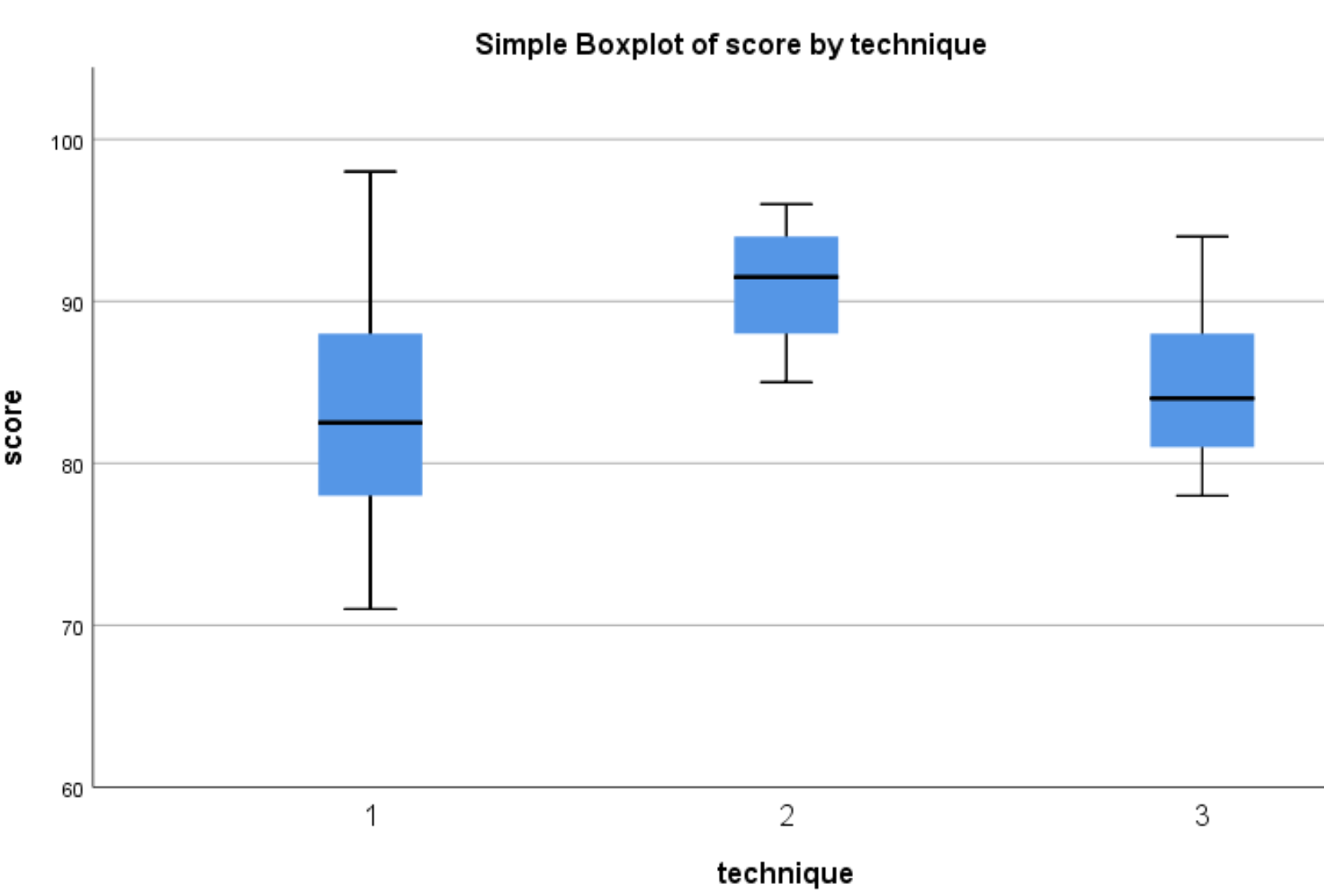
We kunnen zien dat de verdeling van toetsscores doorgaans hoger is voor leerlingen die Techniek 2 gebruikten dan voor leerlingen die Techniek 1 en 3 gebruikten. Om te bepalen of deze scoreverschillen statistisch significant zijn, zullen we een one-way ANOVA uitvoeren.

Stap 2: Voer een eenrichtings-ANOVA uit.

Klik op het tabblad Analyseren , vervolgens op Middelen vergelijken en vervolgens op One-Way ANOVA .

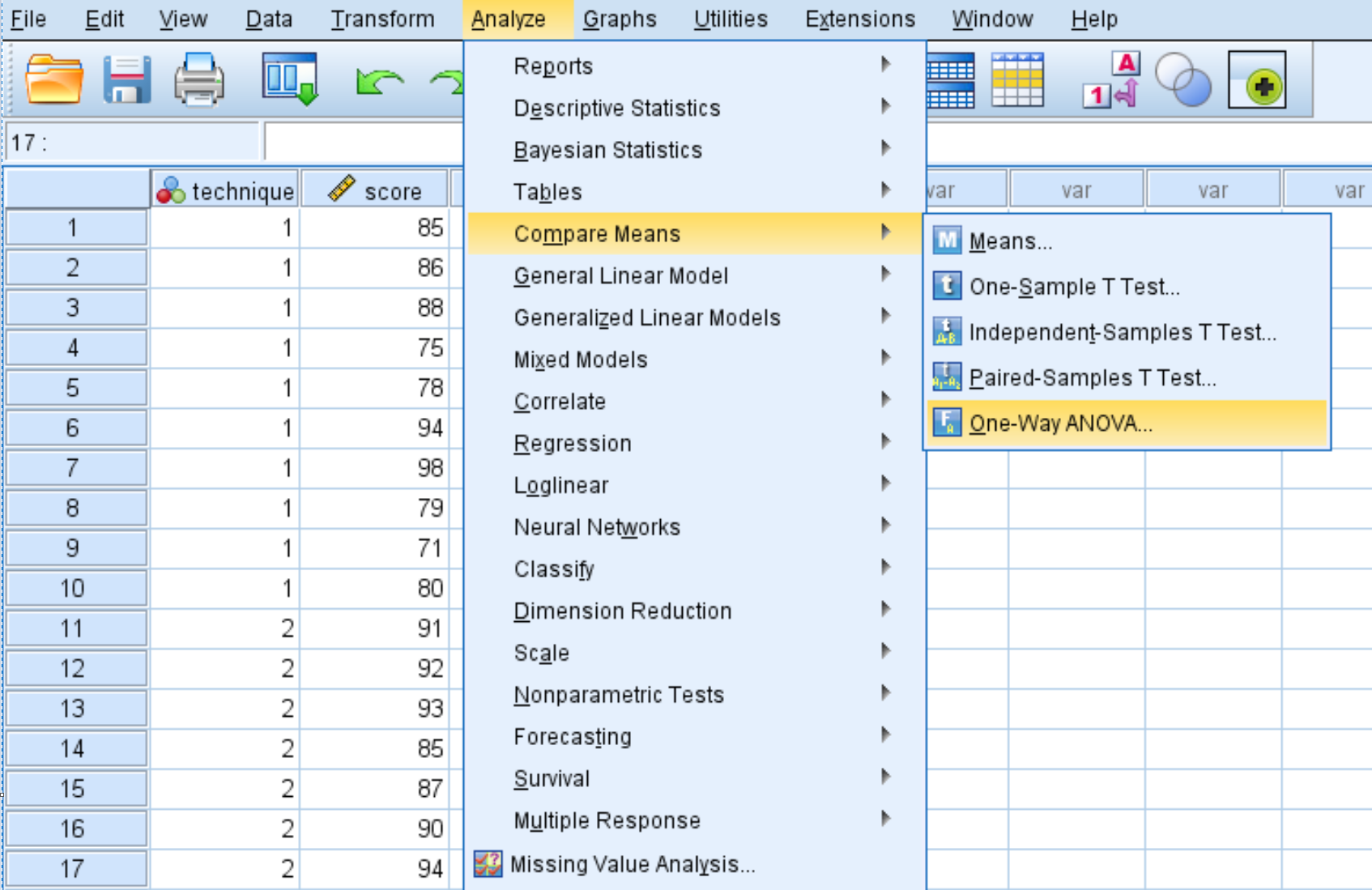
In het nieuwe venster dat verschijnt, plaatst u de variabele score in het vak met de naam Dependent List en de variabele techniek in het vak met de naam Factor.

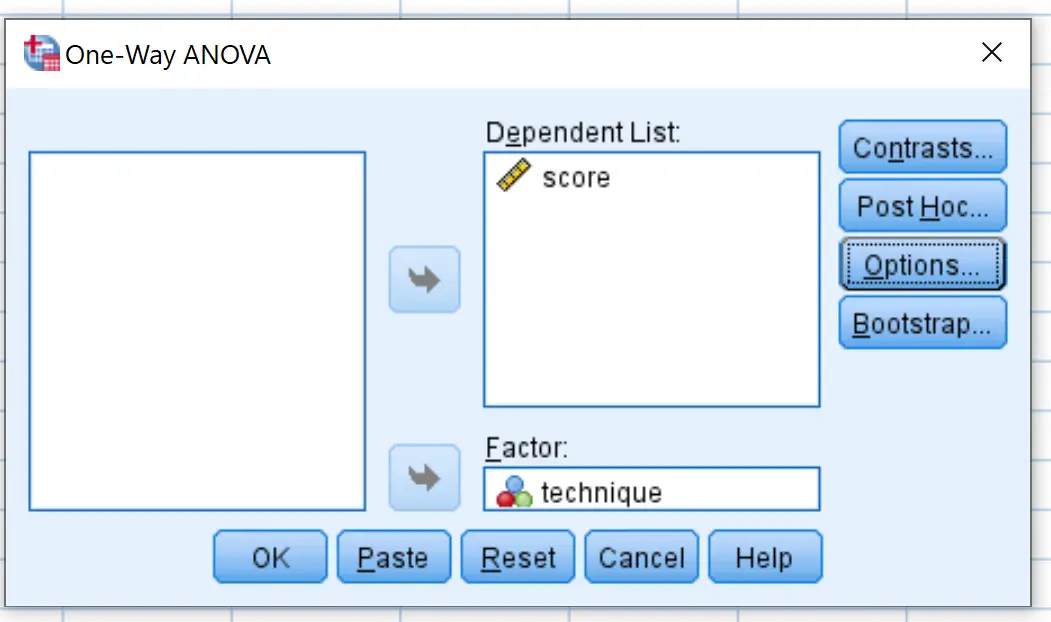
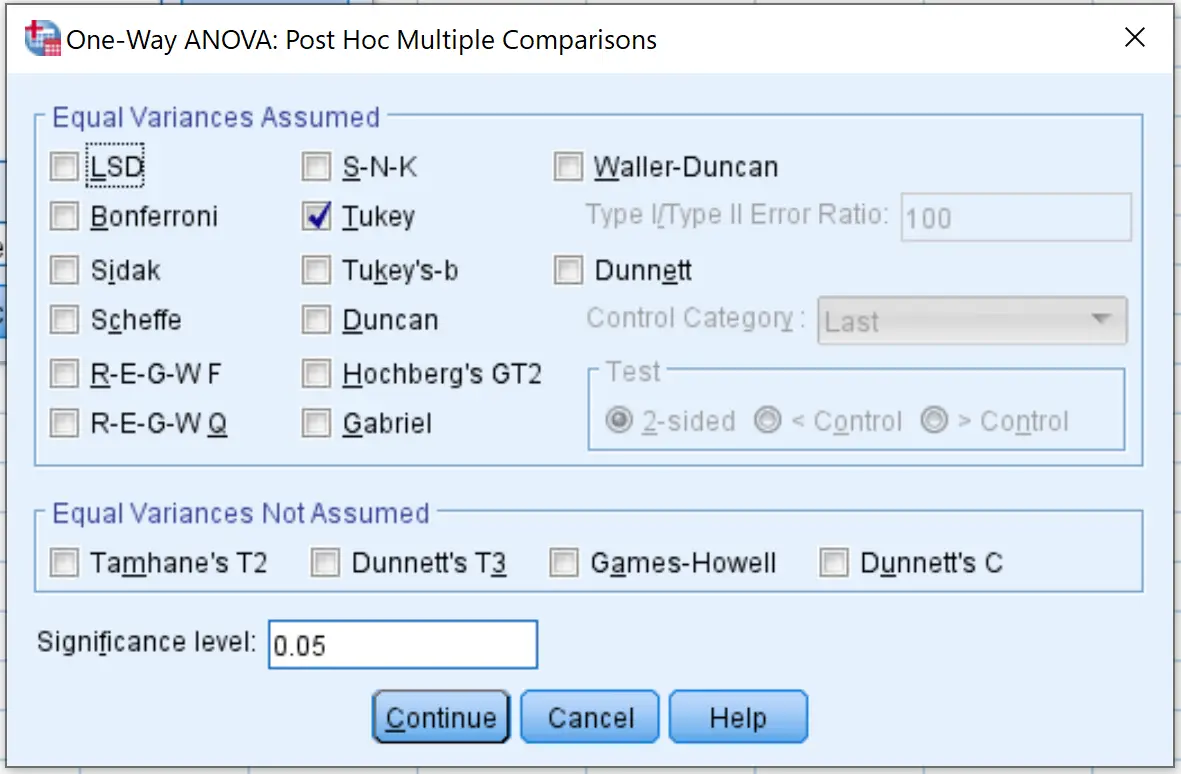
Klik vervolgens op Post Hoc en vink het vakje naast Tukey aan. Klik vervolgens op Doorgaan .

Klik vervolgens op Opties en vink het vakje naast Beschrijvend aan. Klik vervolgens op Doorgaan .

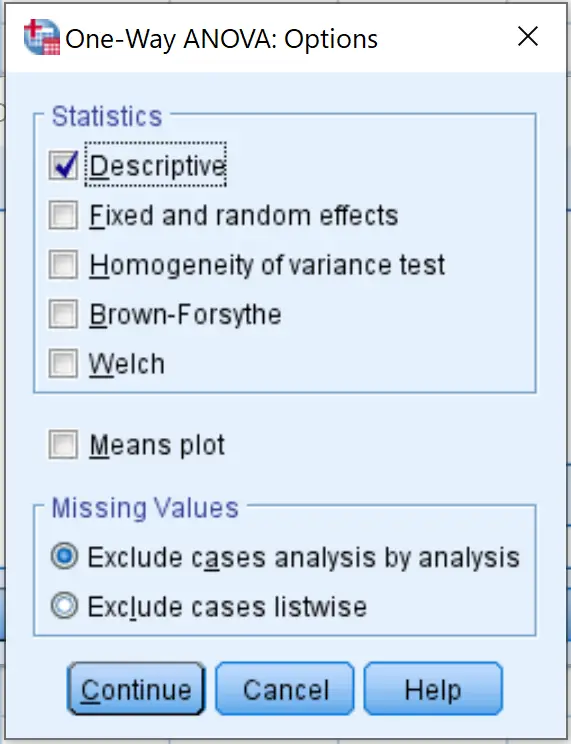
Klik ten slotte op OK .

Stap 3: Interpreteer het resultaat.

Zodra u op OK klikt, verschijnen de eenrichtings-ANOVA-resultaten. Zo interpreteert u het resultaat:

Tabelbeschrijving

Deze tabel toont beschrijvende statistieken voor elk van de drie groepen in onze dataset.

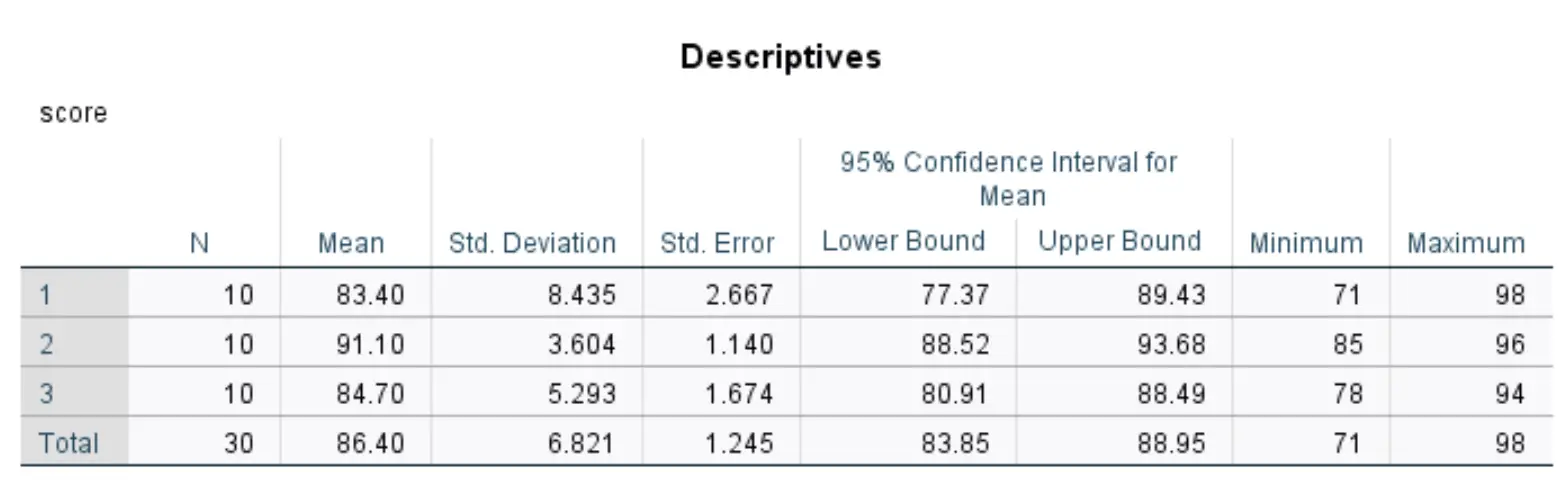
De meest relevante cijfers zijn onder meer:

• N: Het aantal studenten in elke groep.
• Gemiddeld: de gemiddelde testscore voor elke groep.
• Standaard. Afwijking: Standaardafwijking van testresultaten voor elke groep.

ANOVA-tafel

Deze tabel toont de resultaten van de eenrichtings-ANOVA:

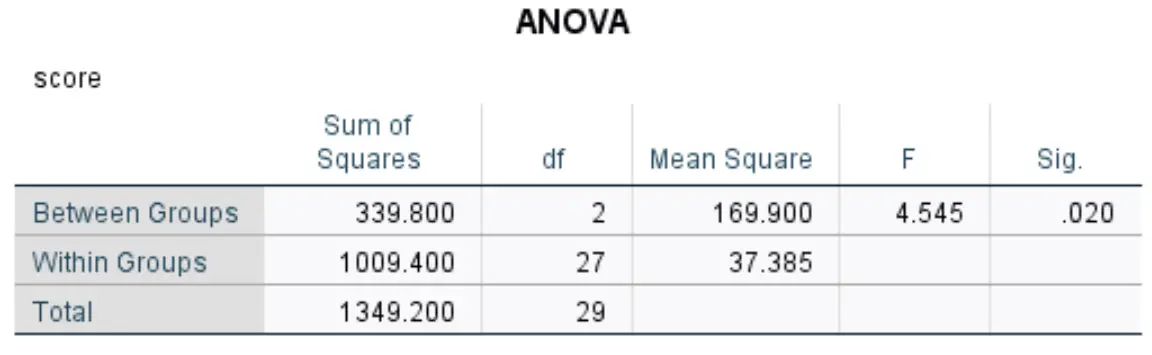
De meest relevante cijfers zijn onder meer:

• F: De algemene F-statistiek.
• Sig: De p-waarde die overeenkomt met de F-statistiek (4,545) met de teller df (2) en de noemer df (27). In dit geval blijkt de p-waarde 0,020 te zijn.

Bedenk dat een eenrichtings-ANOVA de volgende nul- en alternatieve hypothesen gebruikt:

• H ₀ (nulhypothese): μ ₁ = μ ₂ = μ ₃ = … = μ _k (alle populatiegemiddelden zijn gelijk)
• _HA (alternatieve hypothese): ten minste één populatiegemiddelde is anders   rest

Omdat de p-waarde van de ANOVA-tabel kleiner is dan 0,05, hebben we voldoende bewijs om de nulhypothese te verwerpen en te concluderen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Om precies te weten welke groepsgemiddelden van elkaar verschillen, kunnen we de laatste tabel met het ANOVA-resultaat raadplegen.

Meerdere vergelijkingstabel

Deze tabel toont Tukey’s post-hoc meervoudige vergelijkingen tussen elk van de drie groepen. Wij zijn vooral geïnteresseerd in Sig. kolom, die de p-waarden weergeeft voor de verschillen in gemiddelden tussen elke groep:

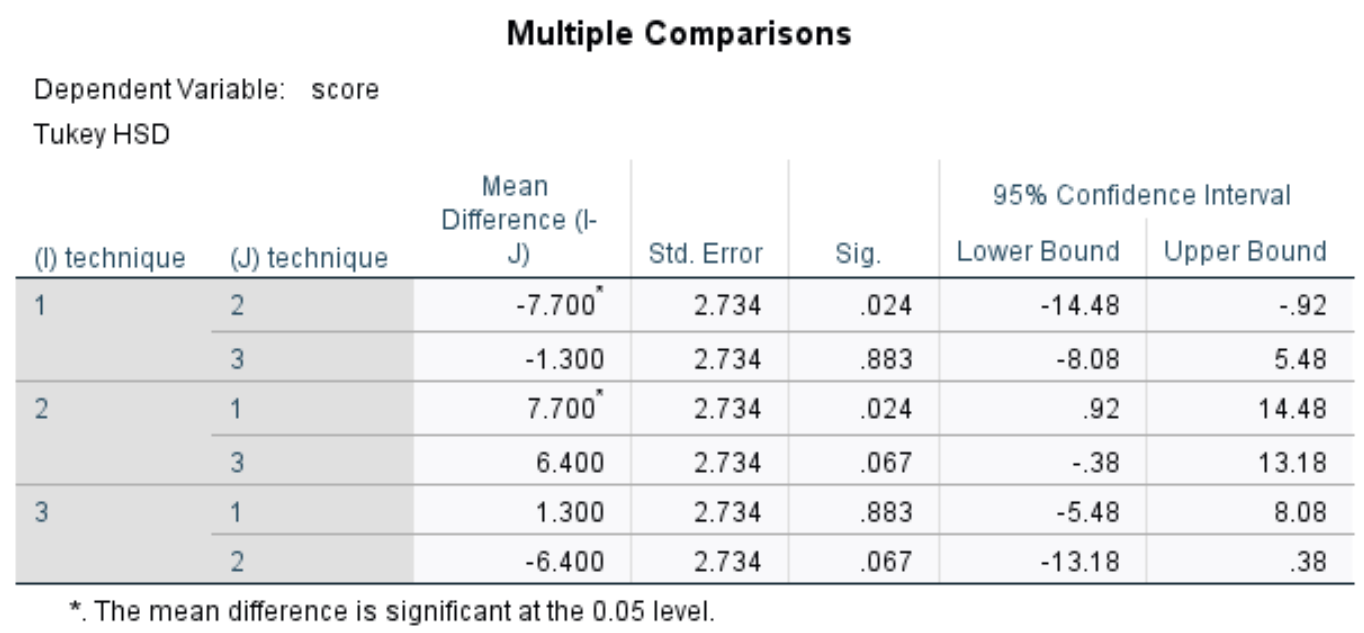
In de tabel kunnen we de p-waarden zien voor de volgende vergelijkingen:

• Techniek 1 tegen 2: | p-waarde = 0,024
• Techniek 1 tegen 3 | p-waarde = 0,883
• Techniek 2 tegen 3 | p-waarde = 0,067

De enige groepsvergelijking met een p-waarde kleiner dan 0,05 vindt plaats tussen Techniek 1 en Techniek 2.

Dit vertelt ons dat er een statistisch significant verschil is in de gemiddelde toetsscores tussen leerlingen die Techniek 1 gebruikten en degenen die Techniek 2 gebruikten.

Er is echter geen statistisch significant verschil tussen techniek 1 en 3, noch tussen techniek 2 en 3.

Stap 4: Rapporteer de resultaten.

Ten slotte kunnen we de resultaten van de one-way ANOVA rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een one-way ANOVA uitgevoerd om te bepalen of drie verschillende onderzoekstechnieken tot verschillende testresultaten leidden.

In totaal gebruikten tien studenten elk van de drie studietechnieken een maand lang voordat ze allemaal dezelfde test aflegden.

Uit een one-way ANOVA bleek dat er een statistisch significant verschil was in testscores tussen ten minste twee groepen (F(2, 27) = 4,545, p = 0,020).

Uit Tukey’s test voor meerdere vergelijkingen bleek dat de gemiddelde testscores significant verschillend waren tussen studenten die techniek 1 en techniek 2 gebruikten (p = 0,024, 95% BI = [-14,48, -0, 92]).

Er was geen statistisch significant verschil tussen scores voor techniek 1 en 3 (p = 0,883) of tussen scores voor techniek 2 en 3 (p = 0,067).