Hoe qq-plots in stata te maken en te interpreteren

Een QQ-plot , een afkorting van „kwantiel-kwantiel“, wordt vaak gebruikt om te evalueren of de residuen van een regressieanalyse normaal verdeeld zijn of niet.

In deze tutorial wordt uitgelegd hoe u een QQ-plot in Stata maakt en interpreteert.

Voorbeeld: QQ-plot in Stata

Voor dit voorbeeld gebruiken we de automatische gegevensset die in Stata is ingebouwd. We zullen een meervoudig lineair regressiemodel toepassen, waarbij mpg en verplaatsing als verklarende variabelen en prijs als responsvariabele worden gebruikt. Vervolgens verkrijgen we de residuen voor het model en maken we een QQ-plot om te zien of de residuen een normale verdeling volgen.

Stap 1: Gegevens laden en weergeven.

Eerst zullen we de gegevens laden met behulp van de volgende opdracht:

automatisch gebruik van het systeem

Vervolgens krijgen we een snel overzicht van de gegevens met behulp van de volgende opdracht:

samenvatten

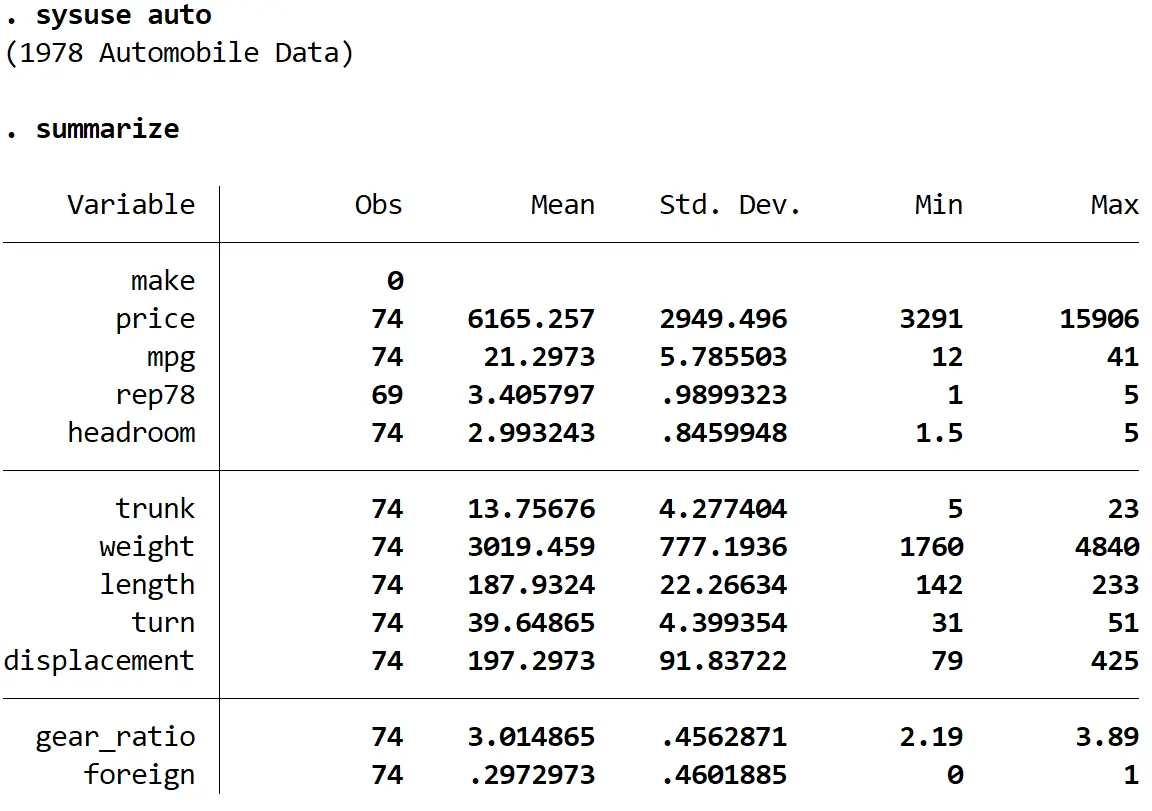
Stap 2: Pas het regressiemodel aan.

Vervolgens zullen we de volgende opdracht gebruiken om het regressiemodel aan te passen:

regressie prijs mpg verplaatsing

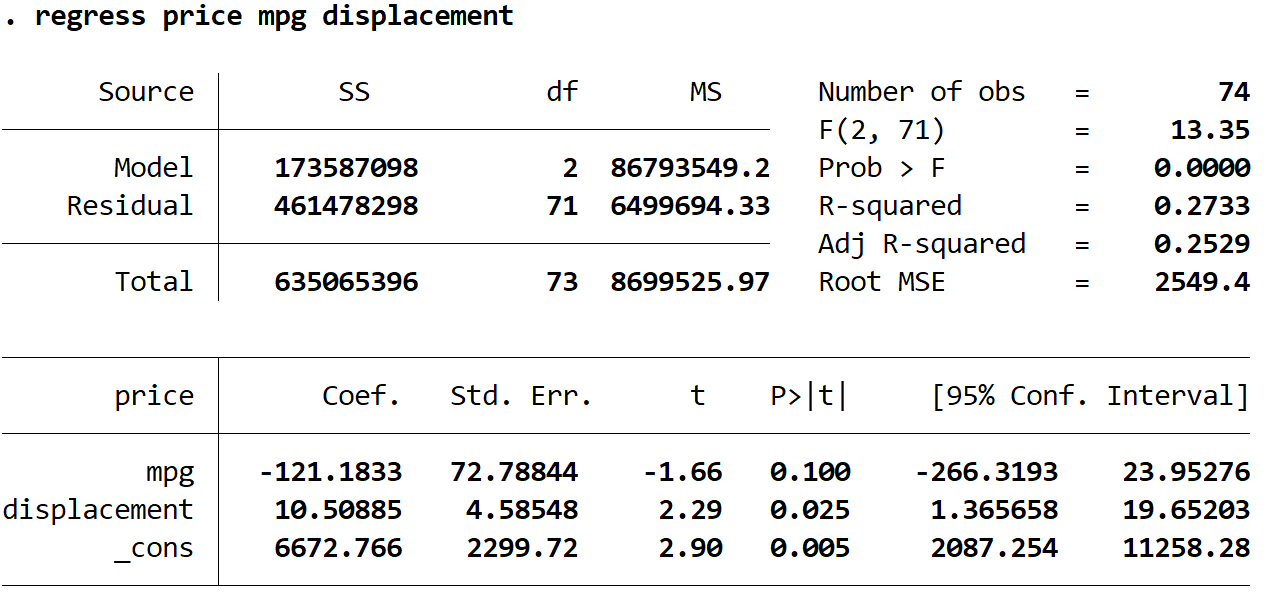
Stap 3: Bereken de residuen .

Bedenk dat een residu simpelweg het verschil is tussen de voorspelde responswaarde (zoals berekend door de geschatte regressievergelijking) en de werkelijke responswaarde.

We kunnen de residuen van elke voorspelling verkrijgen door het commando residuen te gebruiken en deze waarden op te slaan in een variabele met de naam welke we maar willen. In dit geval gebruiken we de naam resid_price :

voorspel verblijfsprijs, residuen

Stap 4: Maak de QQ-plot.

Nu we een lijst met residuen hebben, kunnen we een QQ-plot maken met behulp van de opdracht qnorm :

qnorm prijs_resid

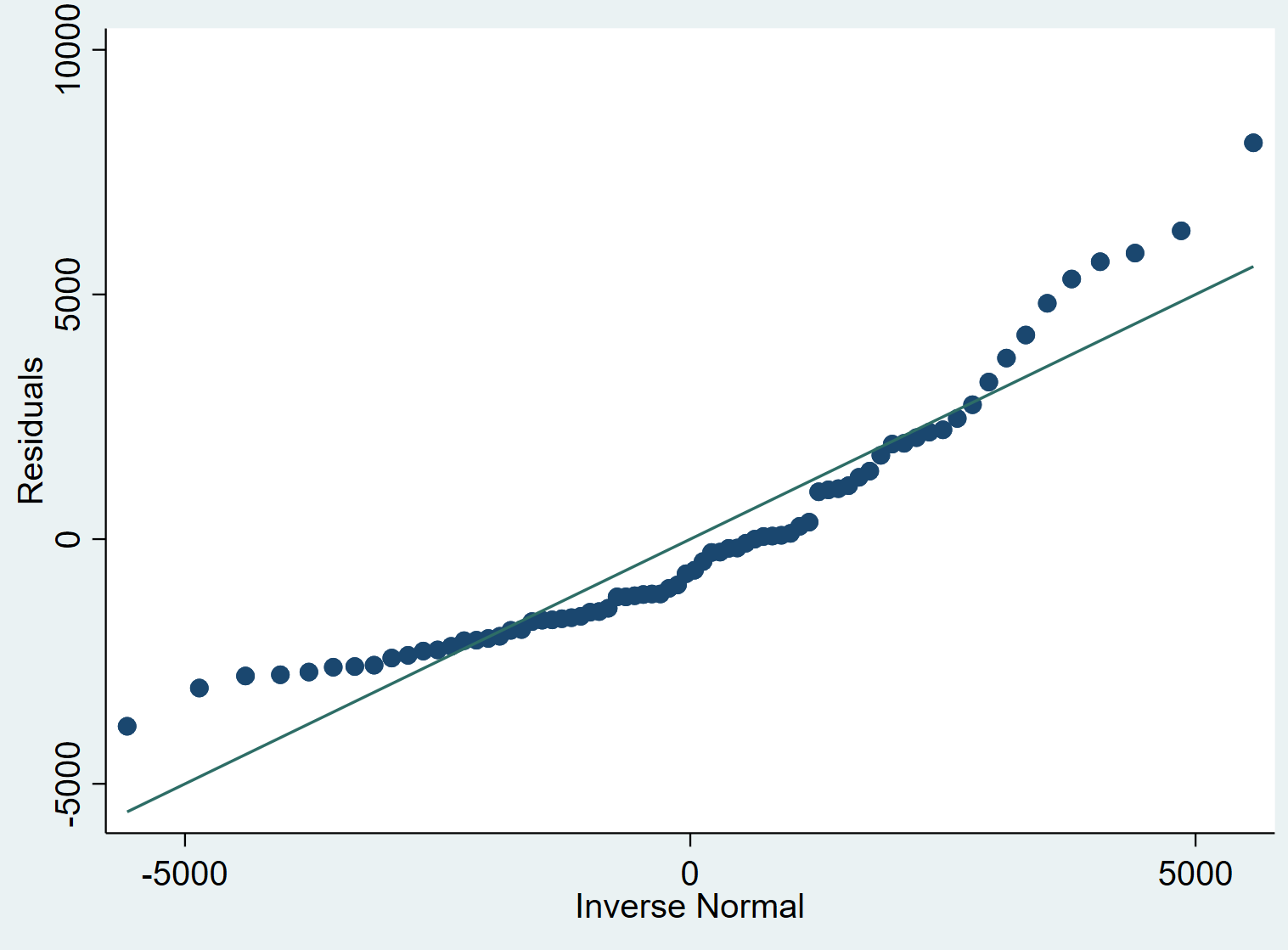
Stap 5: Interpreteer de QQ-plot.

Het idee achter een QQ-plot is eenvoudig: als de residuen een min of meer rechte lijn volgen in een hoek van 45 graden, dan zijn de residuen grofweg normaal verdeeld. We kunnen in onze QQ-grafiek hierboven zien dat de residuen de neiging hebben iets af te wijken van de 45 graden-lijn, vooral aan de uiteinden, wat erop zou kunnen wijzen dat ze niet normaal verdeeld zijn.

Hoewel een QQ-plot geen formele statistische test is, biedt het een eenvoudige manier om visueel te controleren of de residuen normaal verdeeld zijn of niet.

Als blijkt dat uw residuen aanzienlijk afwijken van de 45 graden-lijn in de QQ-grafiek, kunt u overwegen een transformatie uit te voeren op de responsvariabele in uw regressie, bijvoorbeeld met behulp van de vierkantswortel of de log van de responsvariabele.

Als de residuen maar een klein beetje afwijken, hoeft u zich geen zorgen te maken over het transformeren van de responsvariabele, omdat de regressie behoorlijk robuust is voor afwijkingen van de normaliteit.