Wat is de d van somers? (definitie & #038; voorbeeld)

Somers‘ D , een afkorting van Somers‘ Delta, is een maatstaf voor de sterkte en richting van het verband tussen een ordinaal afhankelijke variabele en een ordinaal onafhankelijke variabele.

Een ordinale variabele is een variabele waarin de waarden een natuurlijke volgorde hebben (bijvoorbeeld „slecht“, „neutraal“, „goed“).

De waarde van Somers‘ D ligt tussen -1 en 1 waarbij:

• -1: Geeft aan dat niet alle paren variabelen overeenkomen
• 1: geeft aan dat alle paren variabelen overeenkomen

Somers‘ D wordt in de praktijk gebruikt voor veel niet-parametrische statistische methoden.

Somers‘ D: definitie

Gegeven twee variabelen, X en Y, kunnen we zeggen:

• Twee paren ( _xi , _yi ) en ( _xj , _yj ) zijn concordant als de rangorde van de twee elementen overeenkomt.
• Twee paren (xi _, y _i ) en (x _j , y _j ) zijn dissonant als de rangen van de twee elementen overeenkomen.

We kunnen vervolgens Somers‘ D berekenen met behulp van de volgende formule:

Somers‘ D = ( _NC – N _D ) / ( _NC + N _D + N _T )

Goud:

• N _C : Het aantal overeenkomende paren
• _ND : Het aantal dissonante paren
• N _T : Het aantal gelijke paren

De resulterende waarde ligt altijd tussen -1 en 1.

Somers‘ D: voorbeeld in R

Stel dat een supermarkt de relatie tussen de volgende twee ordinale variabelen wil evalueren:

• Algemene vriendelijkheid van de kassier (gerangschikt van 1 tot 3)
• Algemene tevredenheid over de klantervaring (ook gerangschikt van 1 tot 3)

Ze verzamelen de volgende beoordelingen uit een steekproef van 10 klanten:

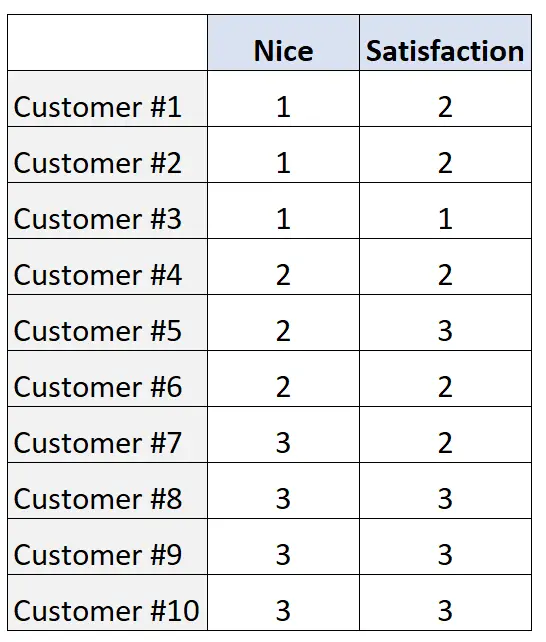
Om de relatie tussen de twee variabelen te kwantificeren, kunnen we Somers‘ D berekenen met behulp van de volgende code in R:

 #enter data
nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3)
satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3)

#load DescTools package
library(DescTools)

#calculate Somers' D
SomersDelta(nice, satisfaction)

[1] 0.6896552

Somers‘ D blijkt 0,6896552 te zijn.

Omdat deze waarde vrij dicht bij 1 ligt, geeft dit aan dat er een vrij sterke positieve relatie bestaat tussen de twee variabelen.

Dit is intuïtief logisch: klanten die kassamedewerkers als aardiger beoordelen, hebben ook de neiging hun algehele tevredenheid hoger te beoordelen.

Aanvullende bronnen

Een inleiding tot de Pearson-correlatiecoëfficiënt
Een inleiding tot Kendall’s Tau