Wat is gebalanceerde nauwkeurigheid? (definitie & #038; voorbeeld)

Evenwichtige nauwkeurigheid is een maatstaf die we kunnen gebruiken om de prestaties van een classificatiemodel te evalueren.

Het wordt als volgt berekend:

Evenwichtige nauwkeurigheid = (gevoeligheid + specificiteit) / 2

Goud:

• Gevoeligheid : het “echte positieve percentage” – het percentage positieve gevallen dat het model kan detecteren.
• Specificiteit : Het “echte negatieve percentage” – het percentage negatieve gevallen dat het model kan detecteren.

Deze metriek is vooral handig wanneer de twee klassen niet in evenwicht zijn, dat wil zeggen dat de ene klasse veel meer voorkomt dan de andere.

Het volgende voorbeeld laat zien hoe u de gebalanceerde nauwkeurigheid in de praktijk kunt berekenen en laat zien waarom dit zo’n nuttige metriek is.

Voorbeeld: Evenwichtige precisie berekenen

Stel dat een sportanalist een logistisch regressiemodel gebruikt om te voorspellen of 400 verschillende universiteitsbasketbalspelers wel of niet zullen worden opgeroepen voor de NBA.

De volgende verwarringsmatrix vat de voorspellingen van het model samen:

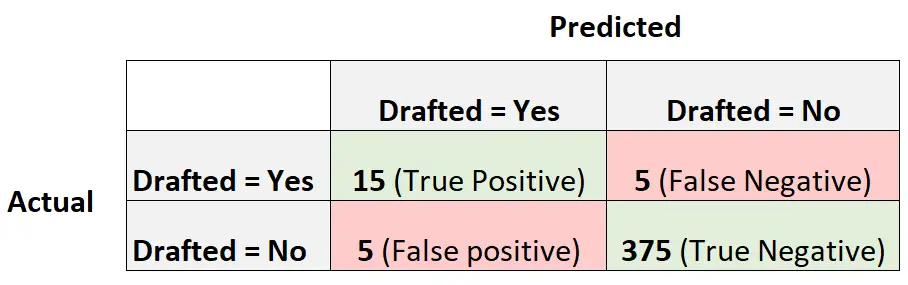
Om de evenwichtige nauwkeurigheid van het model te berekenen, berekenen we eerst de gevoeligheid en specificiteit:

• Gevoeligheid : het “echte positieve percentage” = 15 / (15 + 5) = 0,75
• Specificiteit : Het “echte negatieve percentage” = 375 / (375 + 5) = 0,9868

We kunnen de gebalanceerde precisie dan als volgt berekenen:

• Evenwichtige nauwkeurigheid = (gevoeligheid + specificiteit) / 2
• Gebalanceerde nauwkeurigheid = (0,75 + 9868) / 2
• Gebalanceerde nauwkeurigheid = 0,8684

De gebalanceerde nauwkeurigheid van het model blijkt 0,8684 te zijn.

Merk op dat hoe dichter de uitgebalanceerde precisie bij 1 ligt, hoe beter het model waarnemingen correct kan classificeren.

In dit voorbeeld is de gebalanceerde nauwkeurigheid vrij hoog, wat ons vertelt dat het logistieke regressiemodel heel goed kan voorspellen of universiteitsspelers wel of niet zullen worden opgeroepen voor de NBA.

In dit scenario geeft de gebalanceerde nauwkeurigheid ons een realistischer beeld van de modelprestaties, omdat de klassen erg onevenwichtig zijn (20 spelers waren opgesteld en 380 spelers niet).

We zouden de modelnauwkeurigheid bijvoorbeeld als volgt berekenen:

• Nauwkeurigheid = (TP + TN) / (TP + TN + FP + FN)
• Nauwkeurigheid = (15 + 375) / (15 + 375 + 5 + 5)
• Nauwkeurigheid = 0,975

De nauwkeurigheid van het model is 0,975 , wat extreem hoog lijkt.

Overweeg echter een model dat eenvoudigweg voorspelt dat elke speler niet wordt opgesteld. Het zou een nauwkeurigheid hebben van 380/400 = 0,95 . Dit is slechts iets lager dan de nauwkeurigheid van ons model.

De uitgebalanceerde nauwkeurigheidsscore van 0,8684 geeft ons een beter idee van het vermogen van het model om beide klassen te voorspellen.

Met andere woorden, het geeft ons een beter idee van het vermogen van het model om te voorspellen welke spelers niet zullen worden opgesteld en welke niet.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een verwarringsmatrix maakt in verschillende statistische software:

Hoe u een verwarringsmatrix maakt in Excel
Hoe maak je een verwarringsmatrix in R
Hoe je een verwarringsmatrix creëert in Python