Excel: hoe u lijnsch gebruikt om meervoudige lineaire regressie uit te voeren

U kunt de LIJNSCH- functie in Excel gebruiken om een meervoudig lineair regressiemodel aan een reeks gegevens te koppelen.

Deze functie gebruikt de volgende basissyntaxis:

 = LINEST ( known_y's, [known_x's], [const], [stats] )

Goud:

• bekende_y’s : een array met bekende y-waarden
• bekende_x’s : een array met bekende x-waarden
• const : Optioneel argument. Indien WAAR, wordt constante b normaal verwerkt. Indien ONWAAR, wordt constante b ingesteld op 1.
• stats : Optioneel argument. Indien TRUE worden aanvullende regressiestatistieken geretourneerd. Als FALSE worden er geen aanvullende regressiestatistieken geretourneerd.

Het volgende stap-voor-stap voorbeeld laat zien hoe u deze functie in de praktijk kunt gebruiken.

Stap 1: Voer de gegevens in

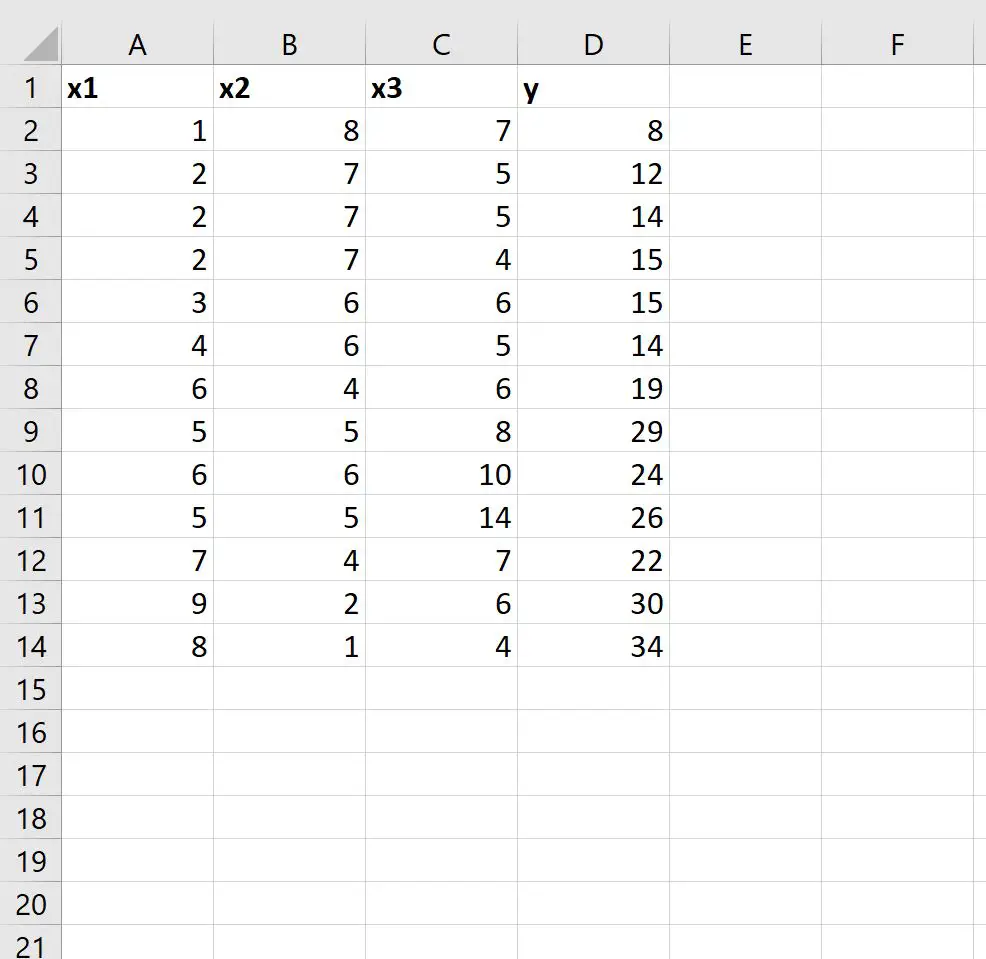
Laten we eerst de volgende gegevensset in Excel invoeren:

Stap 2: Gebruik LIJNSCH om een meervoudig lineair regressiemodel te fitten

Stel dat we een meervoudig lineair regressiemodel willen fitten met behulp van x1 , x2 en x3 als voorspellende variabelen en y als responsvariabele.

Om dit te doen, kunnen we de volgende formule in elke cel typen, zodat deze in dit meervoudige lineaire regressiemodel past

 =LINEST( D2:D14 , A2:C14 )

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken:

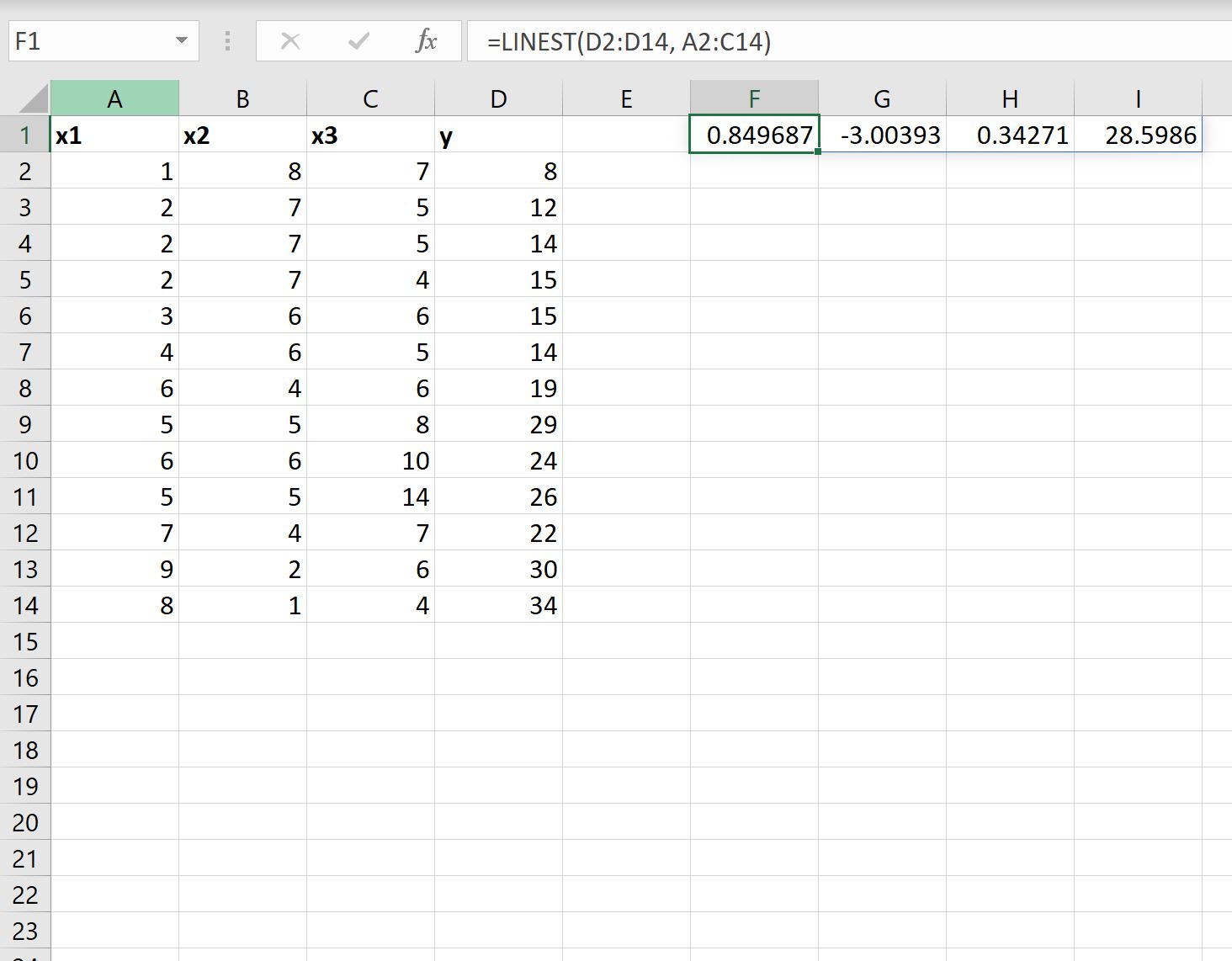
Zo interpreteert u het resultaat:

• De coëfficiënt van het snijpunt is 28,5986 .
• De coëfficiënt voor x1 is 0,34271 .
• De coëfficiënt voor x2 is -3,00393 .
• De coëfficiënt voor x3 is 0,849687 .

Met behulp van deze coëfficiënten kunnen we de aangepaste regressievergelijking als volgt schrijven:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Stap 3 (Optioneel): Bekijk aanvullende regressiestatistieken

We kunnen ook de waarde van het stats- argument in de LIJNSCH- functie gelijk stellen aan TRUE om aanvullende regressiestatistieken weer te geven voor de aangepaste regressievergelijking:

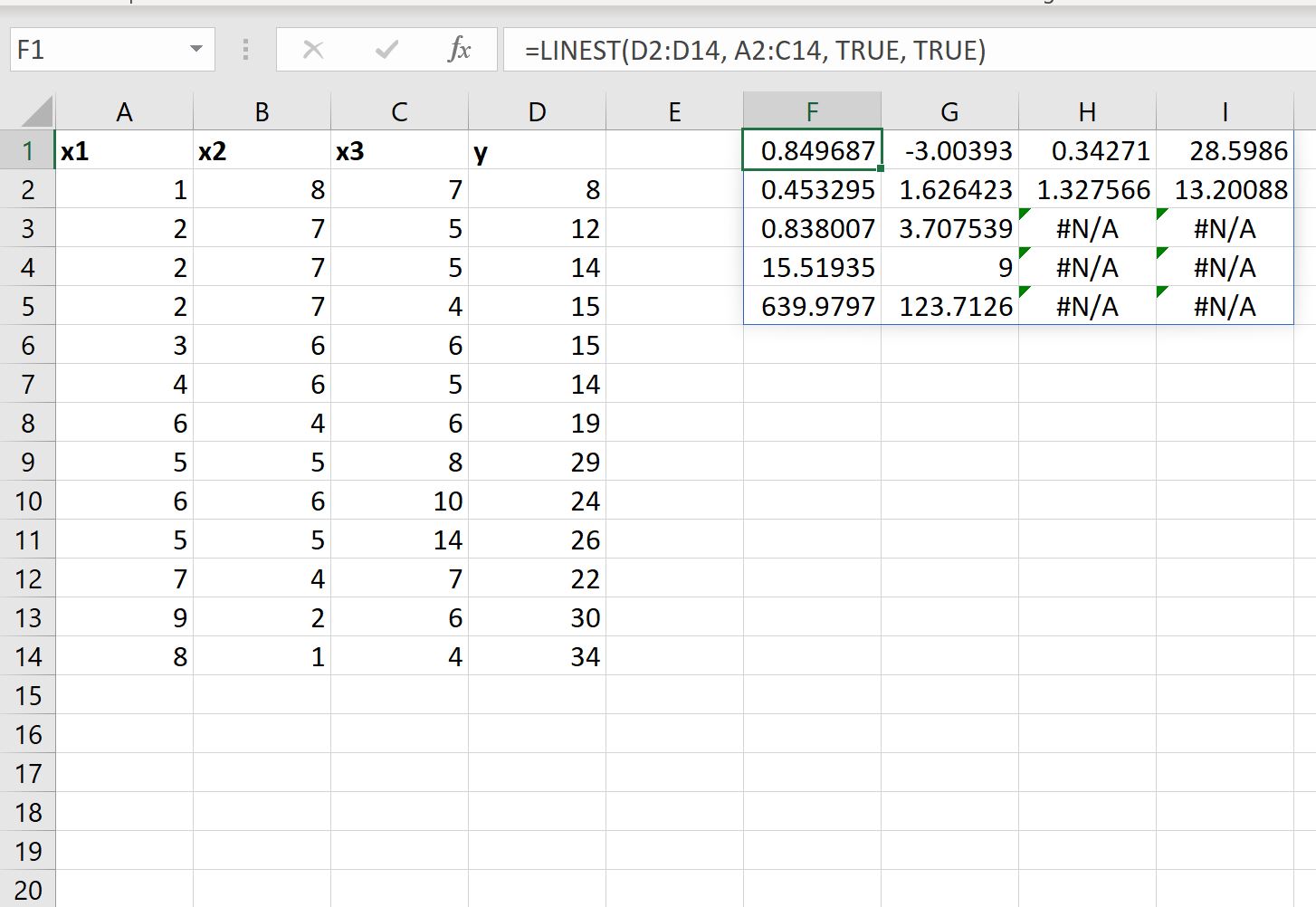
De aangepaste regressievergelijking is nog steeds hetzelfde:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Hier leest u hoe u de andere waarden van het resultaat interpreteert:

• De standaardfout voor x3 is 0.453295 .
• De standaardfout voor x2 is 1.626423 .
• De standaardfout voor x1 is 1.327566 .
• De standaardfout voor het onderscheppen is 13.20088 .
• De R ² van het model is .838007 .
• De resterende standaardfout voor y is 3,707539 .
• De algemene F-statistiek is 15,51925 .
• De vrijheidsgraden zijn 9 .
• De regressiesom van de kwadraten is 639,9797 .
• De resterende kwadratensom is 123,7126 .

Over het algemeen is de maatstaf die in deze aanvullende statistieken het meest interessant is, de ^R2- waarde, die het deel van de variantie in de responsvariabele vertegenwoordigt dat kan worden verklaard door de voorspellende variabele.

De waarde van ^R2 kan variëren van 0 tot 1.

Omdat de R ² van dit specifieke model 0,838 is, vertelt dit ons dat de voorspellende variabelen de waarde van de responsvariabele y goed voorspellen.

Gerelateerd: Wat is een goede R-kwadraatwaarde?

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende bewerkingen in Excel uitvoert:

Hoe de LOGSCH-functie in Excel te gebruiken
Hoe niet-lineaire regressie uit te voeren in Excel
Hoe kubieke regressie uit te voeren in Excel