Hoe de standaardfout van regressie in excel te berekenen

We passen een lineair regressiemodel toe, het model heeft de volgende vorm:

Y = β ₀ + β ₁ X + … + β _ik

waarbij ϵ een foutterm is die onafhankelijk is van X.

Hoe X ook kan worden gebruikt om de waarden van Y te voorspellen, er zullen altijd willekeurige fouten in het model voorkomen.

Eén manier om de spreiding van deze willekeurige fout te meten is door de standaardfout van het regressiemodel te gebruiken, wat een manier is om de standaardafwijking van de residuen ϵ te meten.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe u de standaardfout van een regressiemodel in Excel kunt berekenen.

Stap 1: Creëer de gegevens

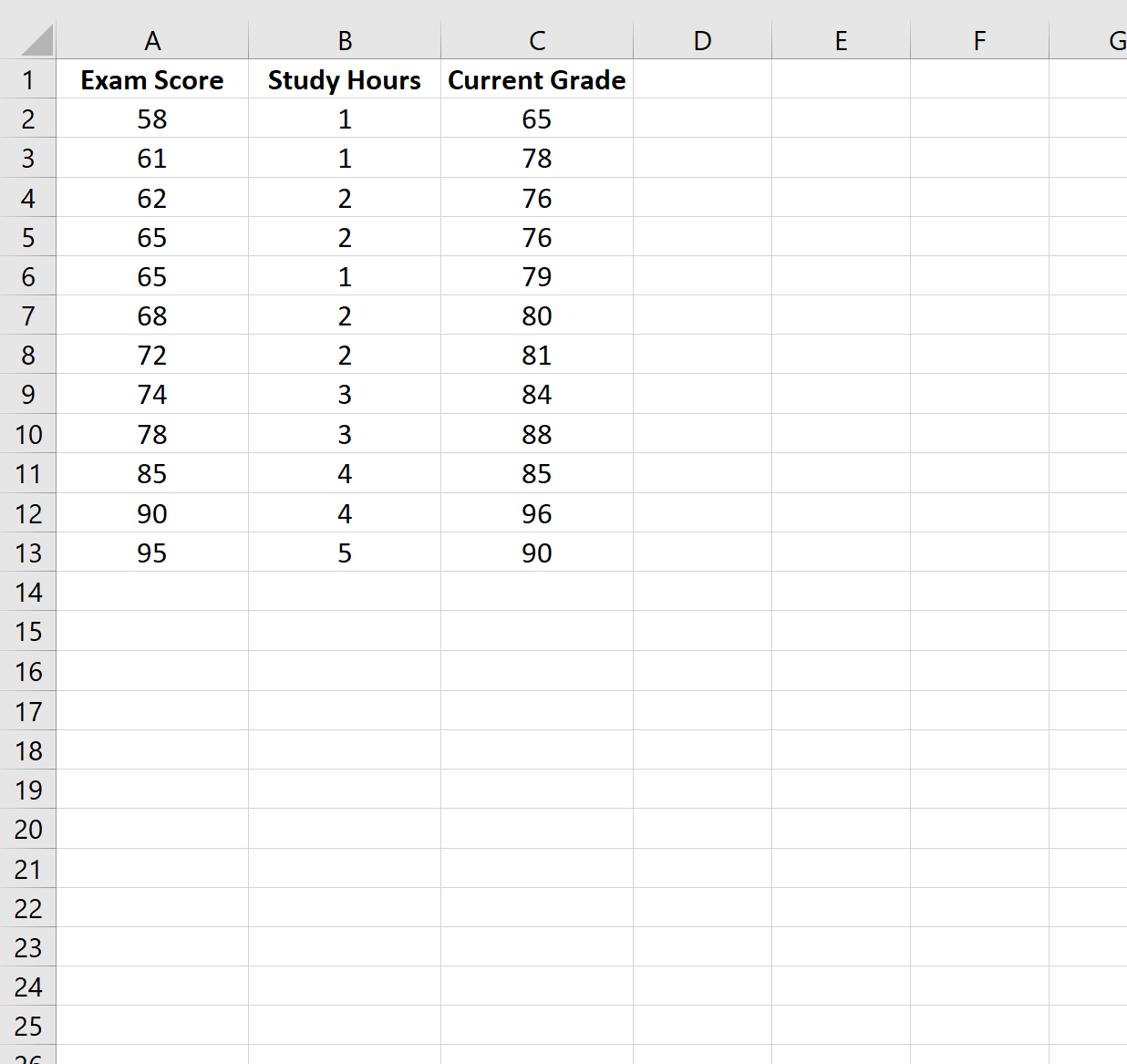
Voor dit voorbeeld maken we een dataset met de volgende variabelen voor 12 verschillende studenten:

• Examenresultaat
• Uren besteed aan studeren
• Huidige klasse

Stap 2: Pas het regressiemodel aan

Vervolgens passen we een meervoudig lineair regressiemodel toe, waarbij we de examenscore alsresponsvariabele gebruiken, en studie-uren en het huidige cijfer als voorspellende variabelen.

Om dit te doen, klikt u op het tabblad Gegevens op het bovenste lint en klikt u vervolgens op Gegevensanalyse :

Als deze optie niet beschikbaar is, moet u eerst het Data Analysis ToolPak laden .

Selecteer Regressie in het venster dat verschijnt. Geef in het nieuwe venster dat verschijnt de volgende informatie op:

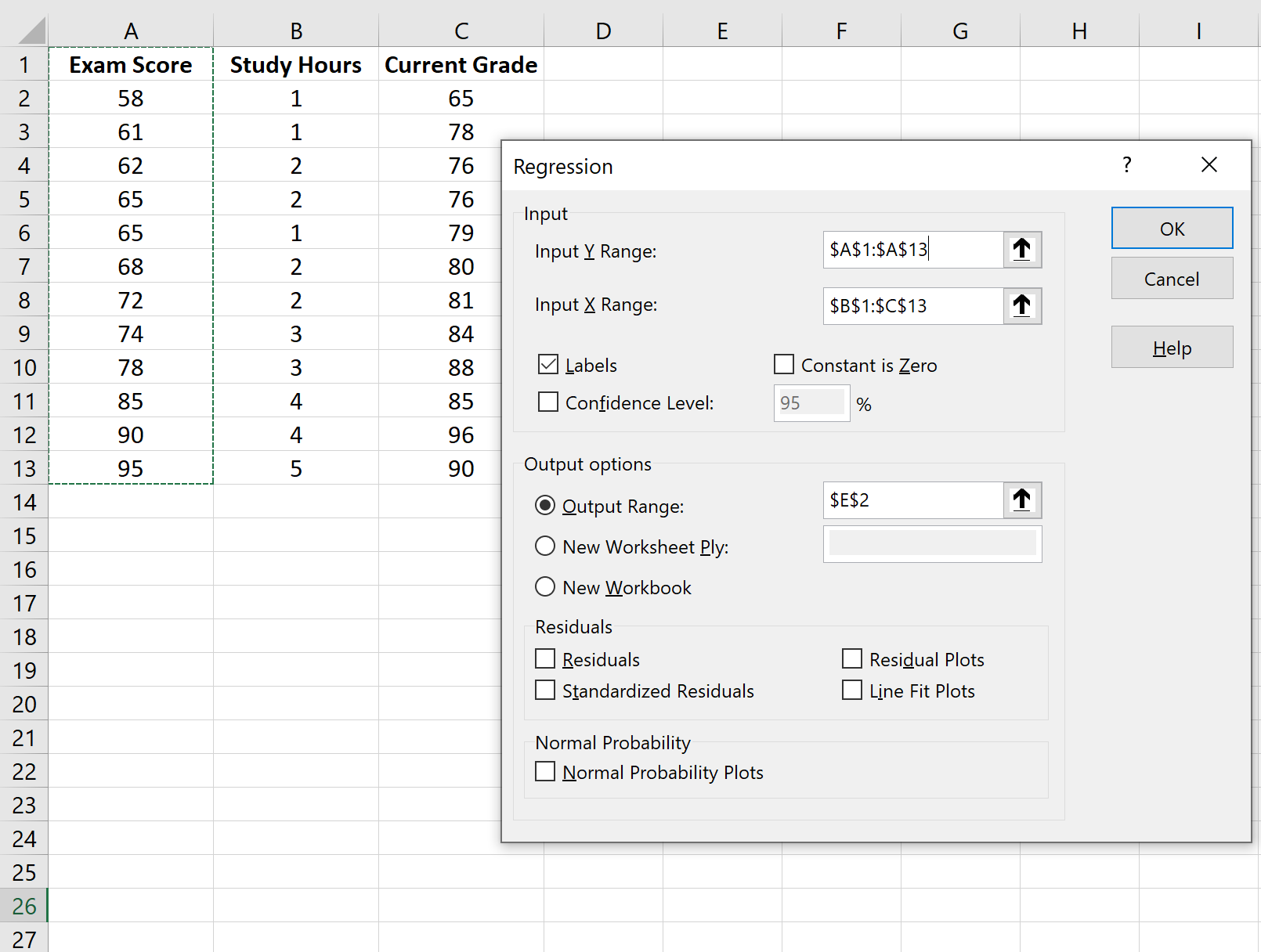
Zodra u op OK klikt, verschijnt de uitvoer van het regressiemodel:

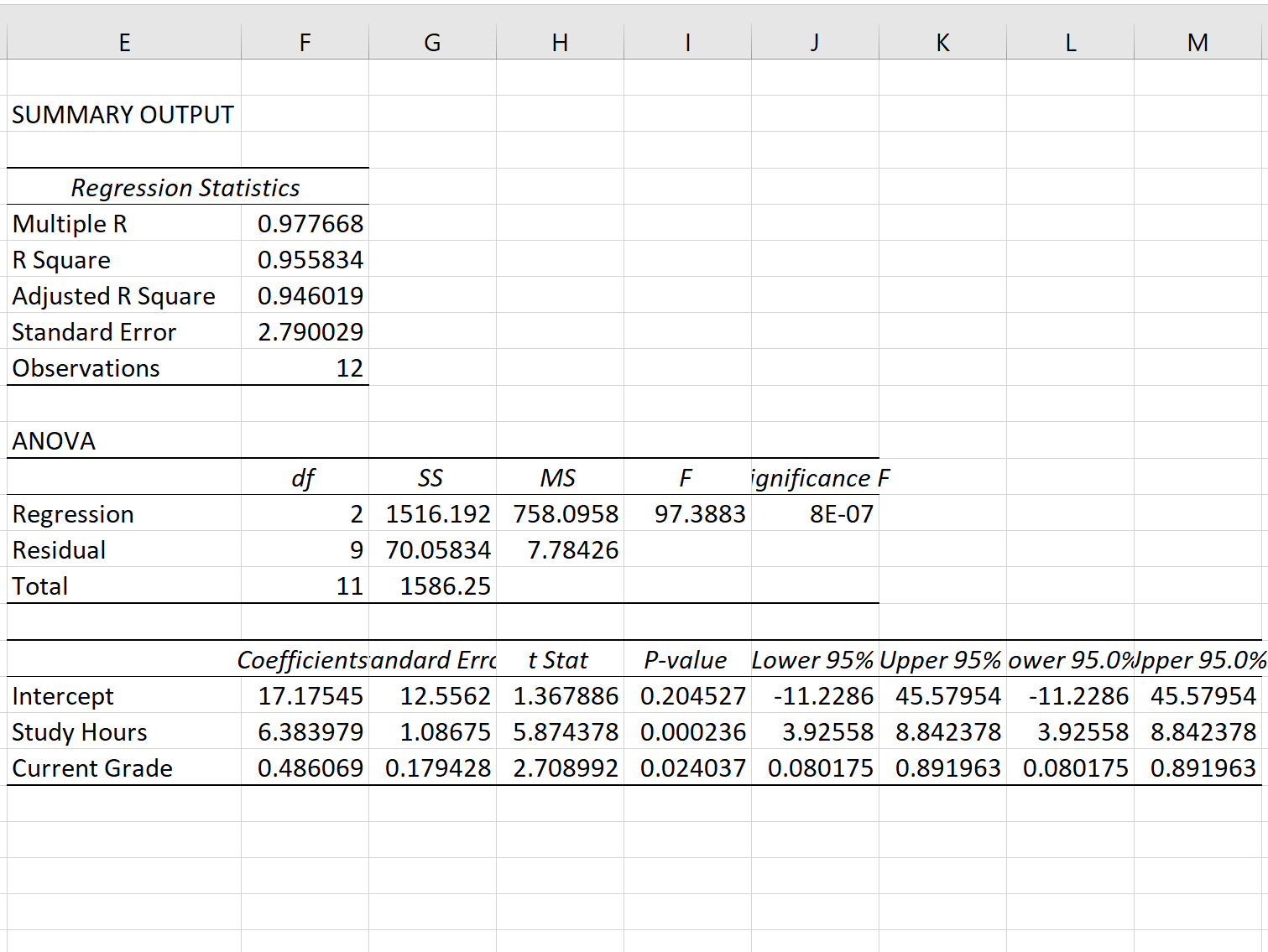
Stap 3: Interpreteer de regressiestandaardfout

De standaardfout van het regressiemodel is het getal naast de standaardfout :

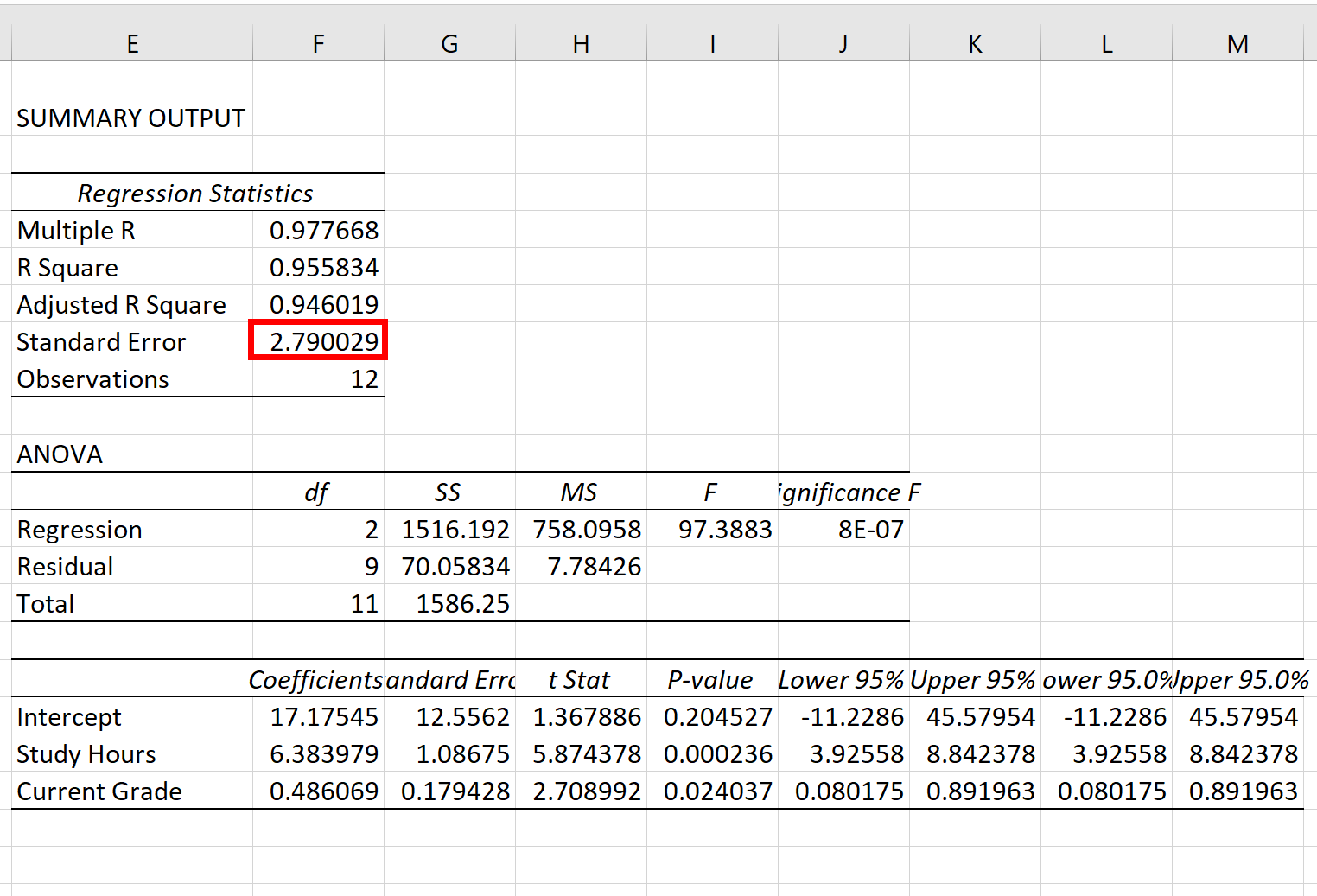
De standaardfout van dit specifieke regressiemodel blijkt 2,790029 te zijn.

Dit getal vertegenwoordigt de gemiddelde afstand tussen de daadwerkelijke examenresultaten en de door het model voorspelde examenresultaten.

Houd er rekening mee dat sommige examenresultaten meer dan 2,79 eenheden verwijderd zullen zijn van de voorspelde score, terwijl andere dichterbij zullen liggen. Maar gemiddeld is de afstand tussen de daadwerkelijke examenresultaten en de voorspelde resultaten 2,790029 .

Merk ook op dat een kleinere standaardfout van regressie aangeeft dat een regressiemodel beter bij een dataset past.

Dus als we een nieuw regressiemodel in de dataset passen en een standaardfout van bijvoorbeeld 4,53 verkrijgen, zou dit nieuwe model minder effectief zijn in het voorspellen van examenscores dan het vorige model.

Aanvullende bronnen

Een andere gebruikelijke manier om de nauwkeurigheid van een regressiemodel te meten is het gebruik van R-kwadraat. Bekijk dit artikel voor een mooie uitleg van de voordelen van het gebruik van de standaardfout van regressie om de nauwkeurigheid versus R-kwadraat te meten.