Hoe de standaardfout van het gemiddelde in excel te berekenen

De standaardfout van het gemiddelde is een manier om de verdeling van waarden in een dataset te meten. Het wordt als volgt berekend:

Standaardfout = s / √n

Goud:

• s : standaardafwijking van het monster
• n : steekproefomvang

U kunt de standaardfout van het gemiddelde van elke gegevensset in Excel berekenen met behulp van de volgende formule:

= STDEV (waardenbereik) / SQRT ( COUNT (waardenbereik))

In het volgende voorbeeld ziet u hoe u deze formule gebruikt.

Voorbeeld: standaardfout in Excel

Stel dat we de volgende dataset hebben:

De volgende schermafbeelding laat zien hoe u de standaardfout van het gemiddelde voor deze gegevensset kunt berekenen:

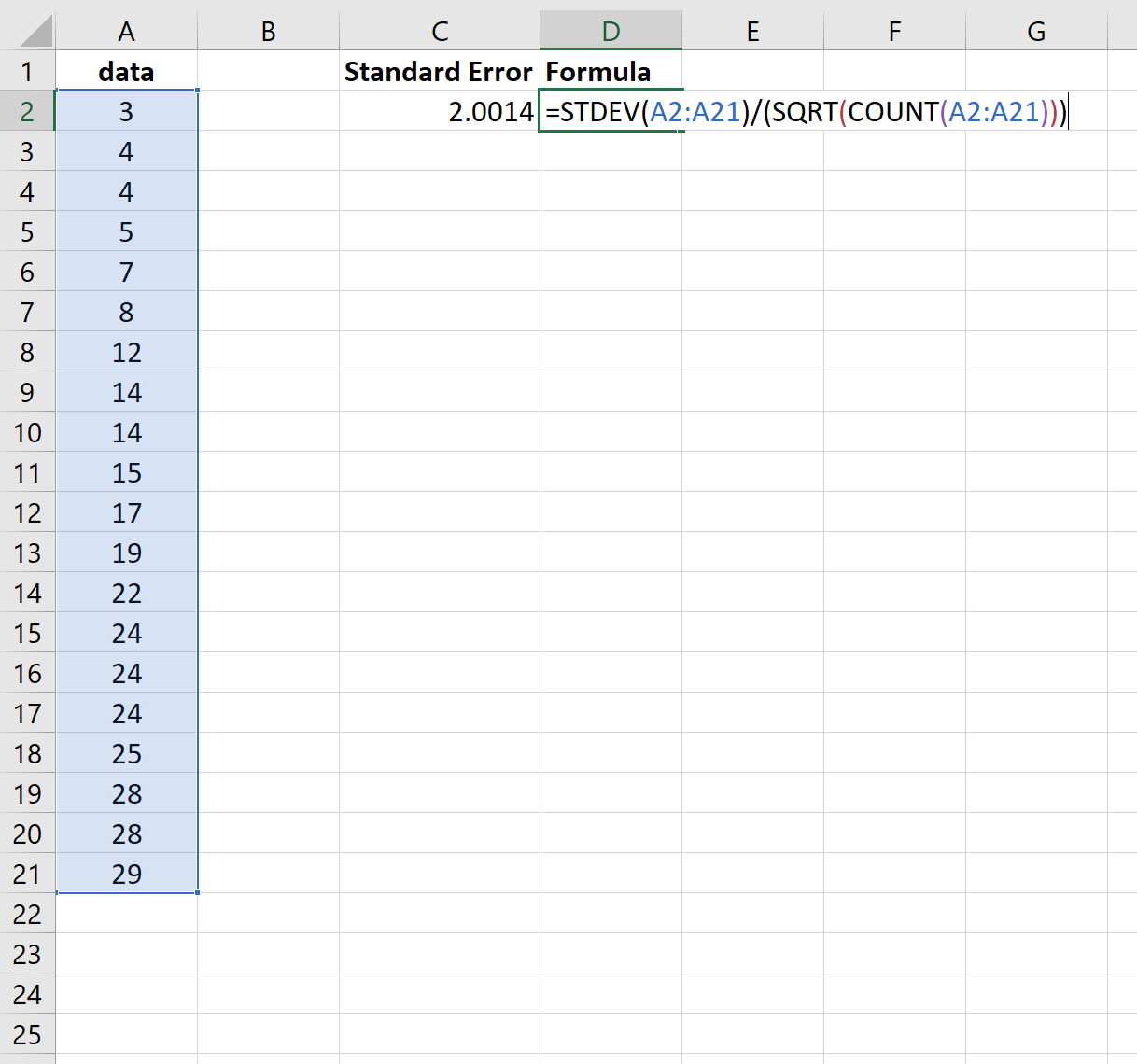
De standaardfout blijkt 2.0014 te zijn.

Houd er rekening mee dat de functie =STDEV() het steekproefgemiddelde berekent, wat equivalent is aan de functie =STDEV.S() in Excel.

We hadden dus de volgende formule kunnen gebruiken om dezelfde resultaten te verkrijgen:

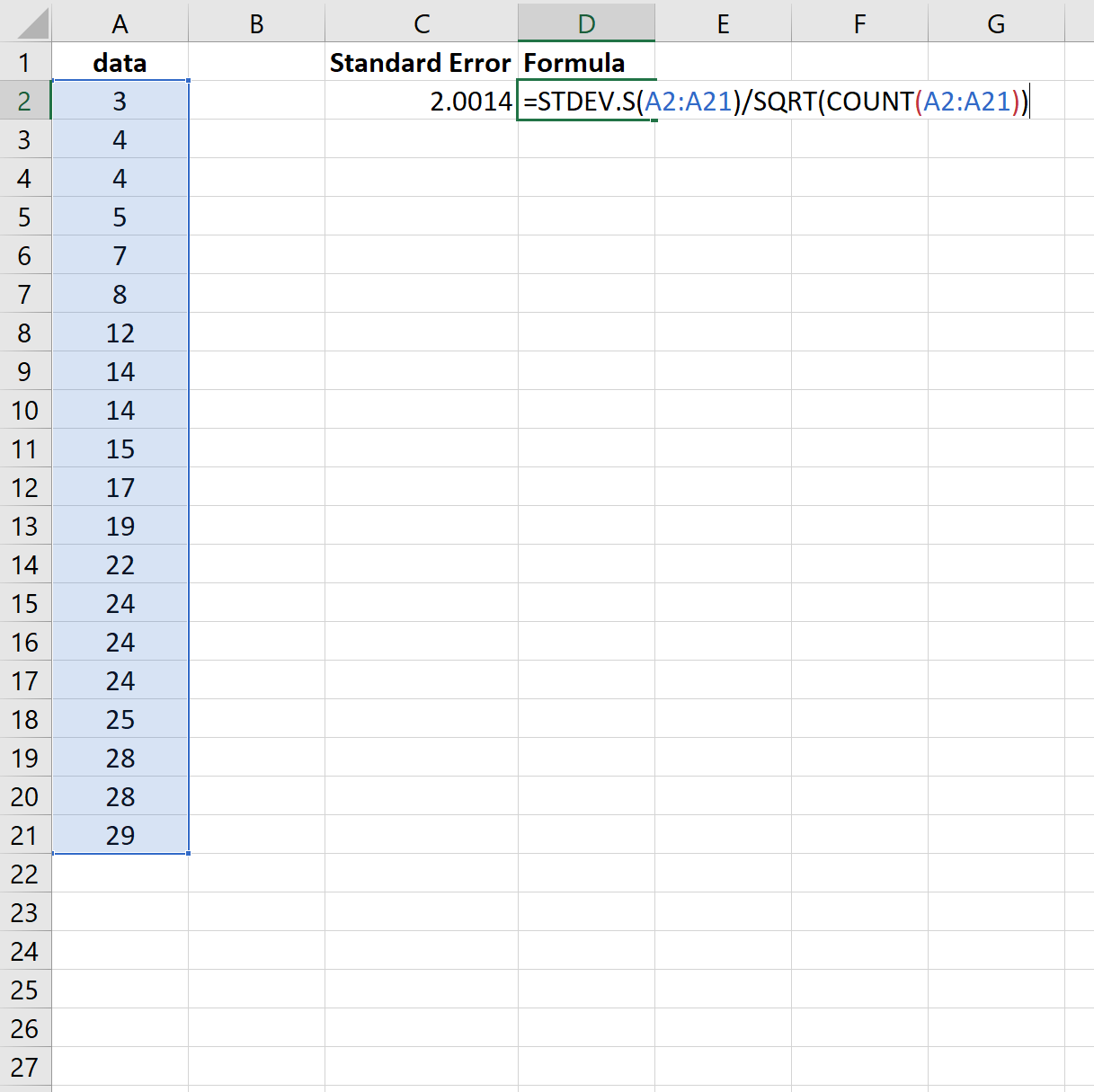
Opnieuw blijkt de standaardfout 2.0014 te zijn.

Hoe de standaardfout van het gemiddelde te interpreteren

De standaardfout van het gemiddelde is eenvoudigweg een maatstaf voor de spreiding van waarden rond het gemiddelde. Er zijn twee dingen waarmee u rekening moet houden bij het interpreteren van de standaardfout van het gemiddelde:

1. Hoe groter de standaardfout van het gemiddelde, hoe meer verspreid de waarden rond het gemiddelde in een dataset liggen.

Om dit te illustreren, overweeg of we de laatste waarde van de vorige dataset met een veel groter getal veranderen:

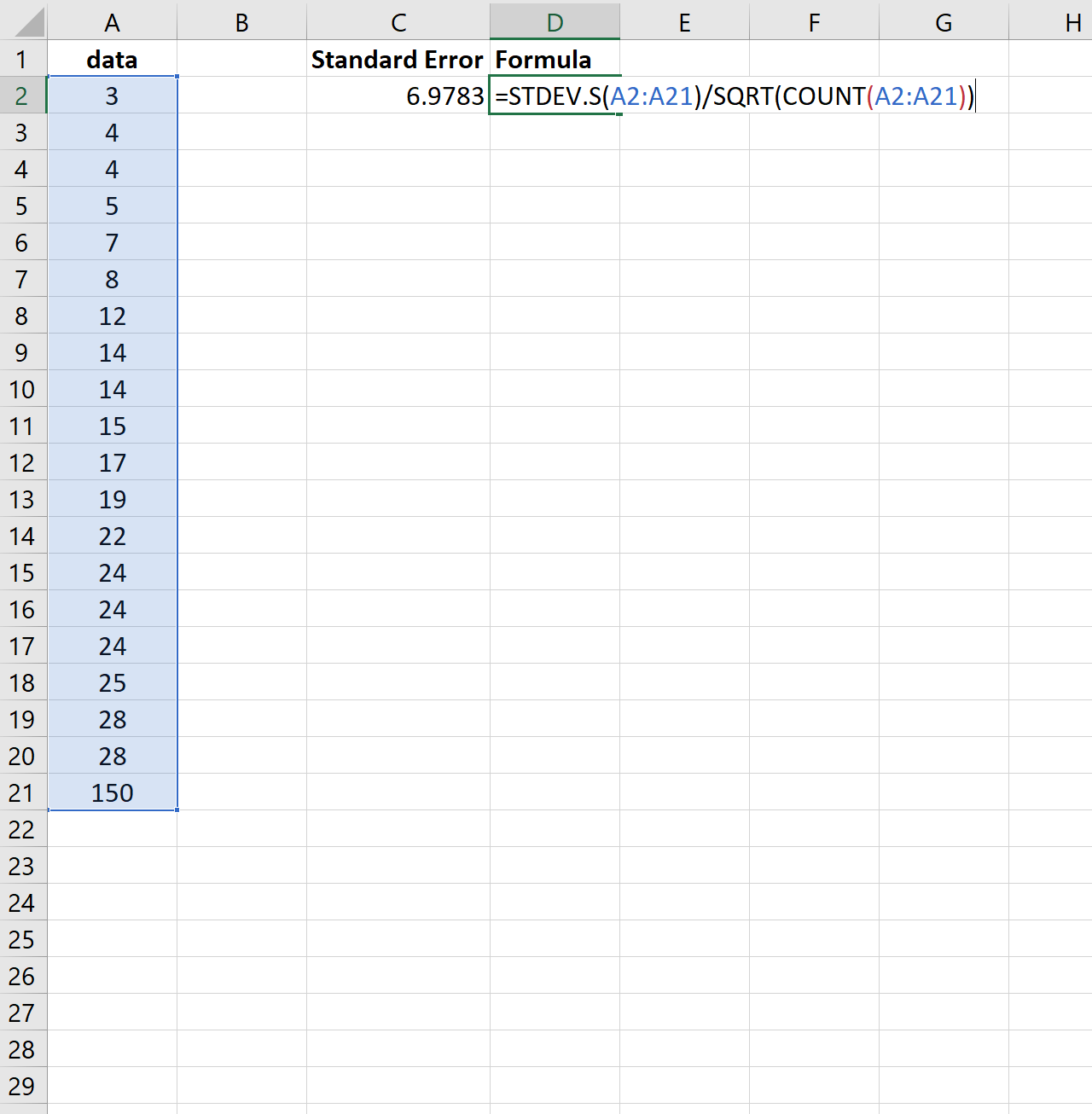
Merk op hoe de standaardfout toeneemt van 2.0014 naar 6.9783 . Dit geeft aan dat de waarden in deze dataset meer rond het gemiddelde verdeeld zijn vergeleken met de vorige dataset.

2. Naarmate de steekproefomvang toeneemt, neigt de standaardfout van het gemiddelde af te nemen.

Om dit te illustreren, beschouwen we de standaardfout van het gemiddelde voor de volgende twee sets gegevens:

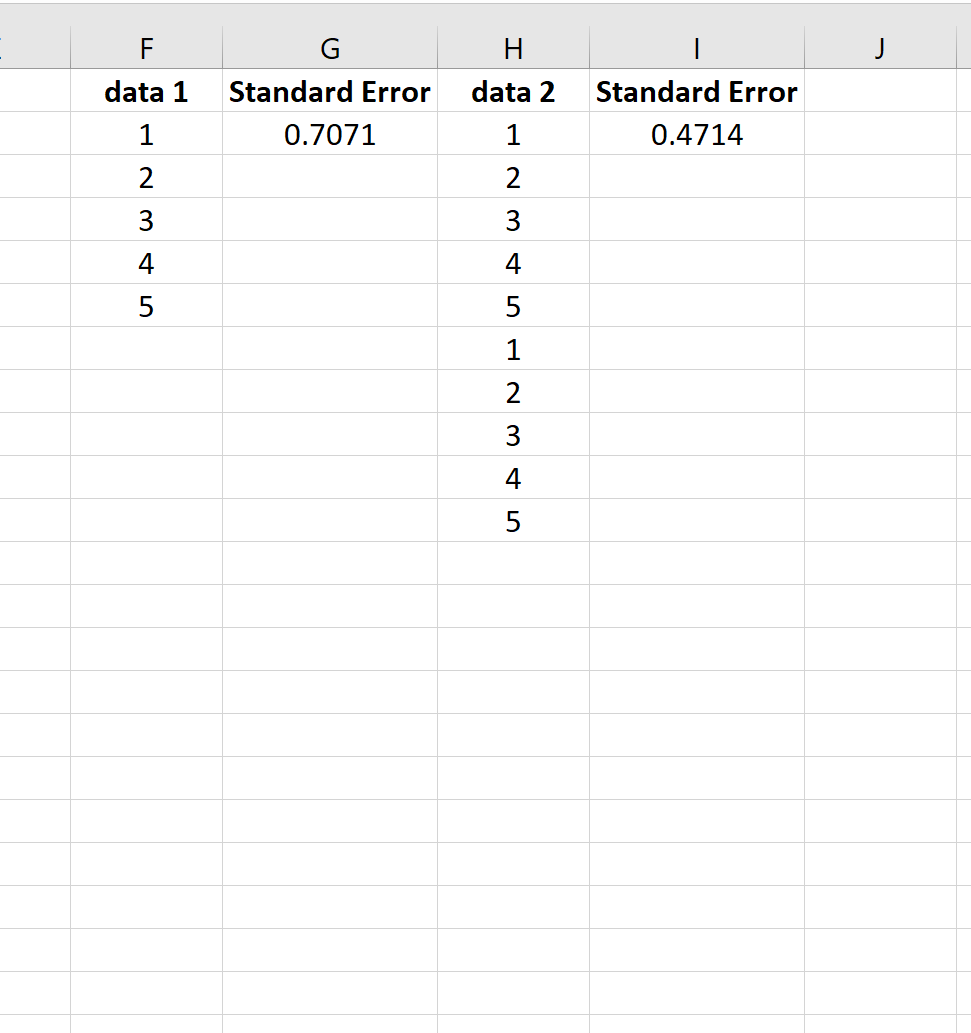
De tweede dataset is eenvoudigweg de eerste dataset die twee keer wordt herhaald. Beide datasets hebben dus hetzelfde gemiddelde, maar de tweede dataset heeft een grotere steekproefomvang en heeft daarom een kleinere standaardfout.