Excel: maak een statistische vergelijking van twee gegevenssets

Vaak wilt u misschien een statistische vergelijking van twee datasets in Excel uitvoeren om te begrijpen hoe de verdeling van waarden in elke dataset verschilt.

Er zijn twee veelgebruikte manieren om een statistische vergelijking uit te voeren:

Methode 1: Bereken de vijfcijferige samenvatting van elke dataset

We kunnen de samenvatting van vijf cijfers van elke dataset berekenen, die uit de volgende waarden bestaat:

• De minimumwaarde
• Het eerste kwartiel (25e percentiel)
• De mediaan (50e percentiel)
• Het derde kwartiel (75e percentiel)
• Het maximum

Door deze vijf waarden te berekenen, kunnen we een goed inzicht krijgen in de verdeling van waarden in elke dataset.

Methode 2: Bereken het gemiddelde en de standaarddeviatie

Een eenvoudiger manier om een statistische vergelijking van twee datasets uit te voeren, is door het gemiddelde en de standaardafwijking van elke dataset te berekenen.

Dit helpt ons te begrijpen waar de ‘centrale’ waarde ongeveer ligt en wat de verdeling van de waarden in elke dataset is.

Het volgende voorbeeld laat zien hoe u elk van deze methoden in de praktijk kunt gebruiken.

Voorbeeld: Voer een statistische vergelijking uit van twee gegevenssets in Excel

Stel dat we in Excel twee sets gegevens hebben die de resultaten tonen van studenten uit twee verschillende klassen die zijn behaald op een bepaald examen:

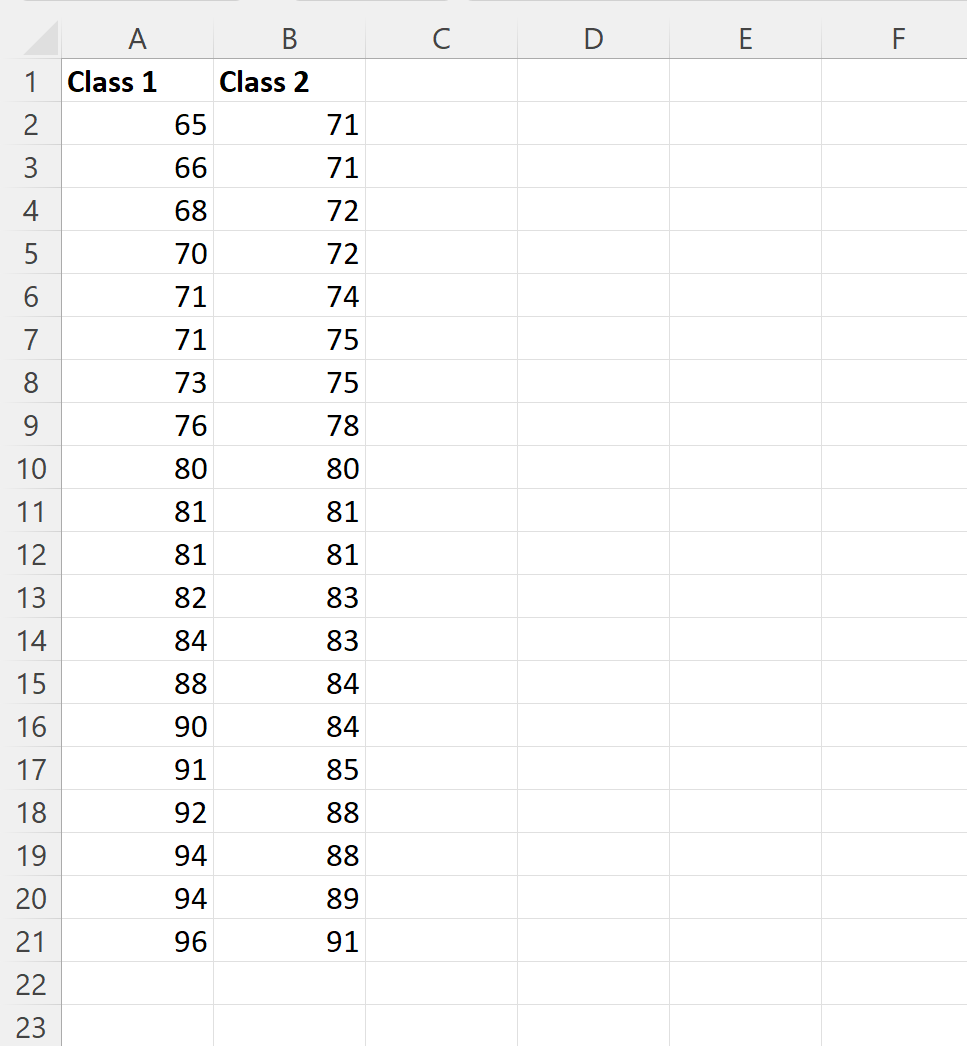
We kunnen de volgende formules in de cellen van kolom E typen om de vijfcijferige samenvatting van de examenresultaten voor klas 1 te berekenen:

• E2 : =MIN(A2:A21)
• E3 : =KWARTIEL(A2:A21, 1)
• E4 : =MEDIAAN(A2:A21)
• E5 : =KWARTIEL(A2:A21, 3)
• E6 : =MAX(A2:A21

We kunnen deze formules vervolgens naar rechts klikken en slepen om dezelfde waarden voor klasse 2 te berekenen:

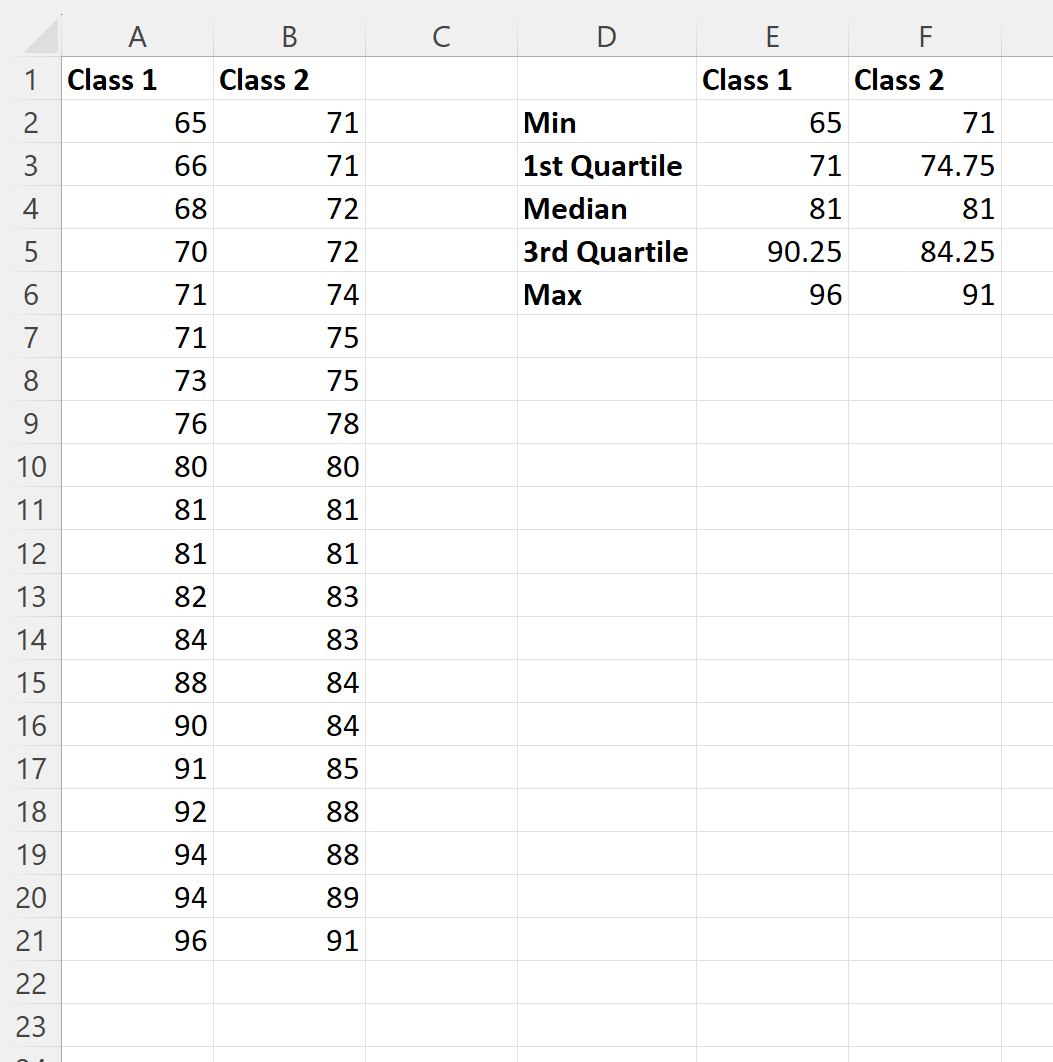
We kunnen dan de volgende formules in de cellen van kolom E invoeren om het gemiddelde en de standaardafwijking van de examenresultaten voor Klasse 1 te berekenen:

• E8 : =GEMIDDELD(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

We kunnen deze formules vervolgens naar rechts klikken en slepen om dezelfde waarden voor klasse 2 te berekenen:

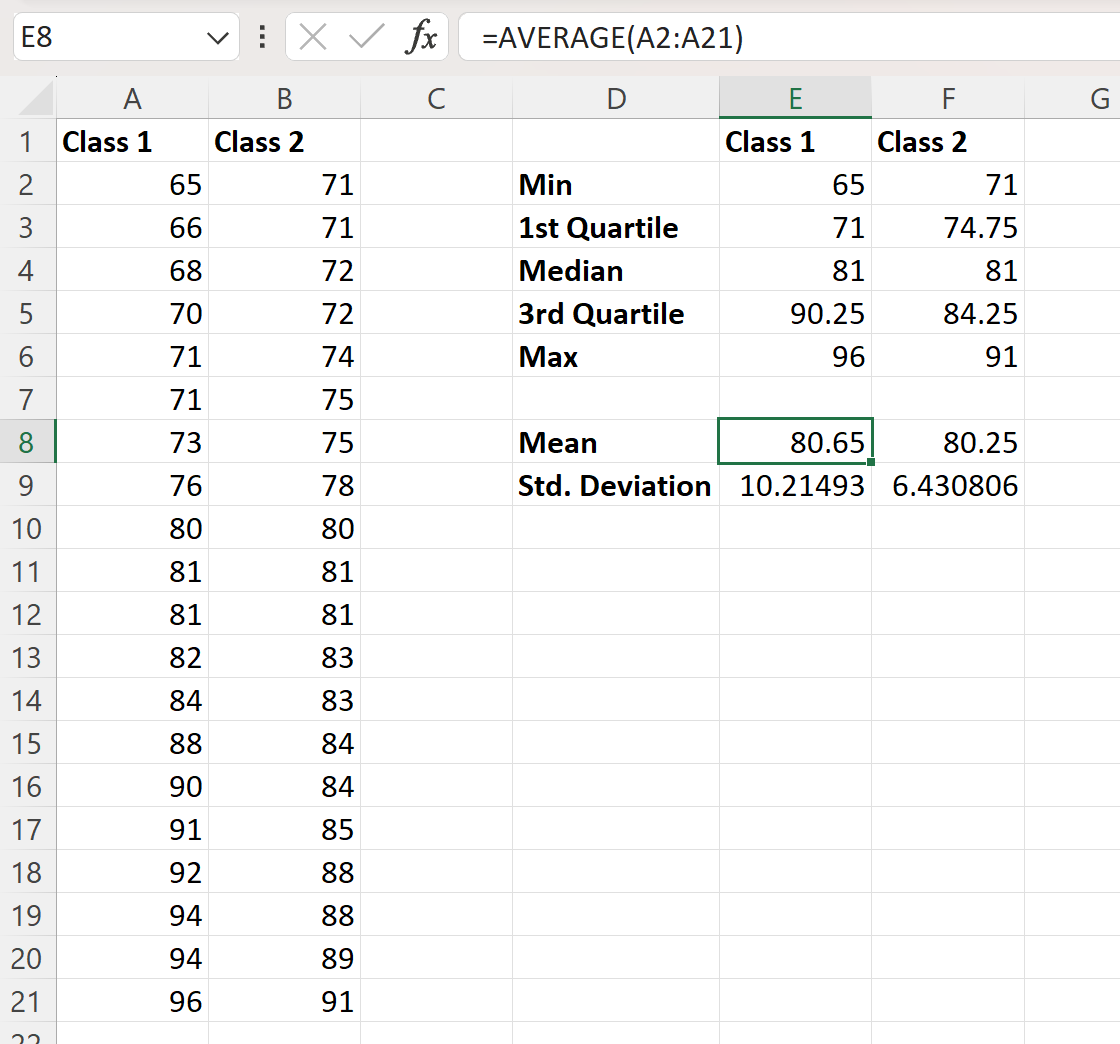
Uit deze statistische vergelijking van de twee datasets kunnen we de volgende conclusies trekken:

Conclusie 1: Beide datasets hebben een vergelijkbare ‘kernwaarde’.

Beide datasets hebben een mediane examenscore van 81. De gemiddelde waarden verschillen slechts weinig: de eerste klas heeft een gemiddelde examenscore van 80,65 terwijl de tweede klas een gemiddelde examenscore heeft van 80,65 terwijl de tweede klas een gemiddelde examenscore heeft van 80.65 ‚ beoordeling van 80.25.

Dit vertelt ons dat de “kern” of “typische” examenscore tussen de twee klassen vergelijkbaar is.

Conclusie 2: De eerste dataset heeft een veel grotere “spreiding” van waarden.

Verschillende indicatoren vertellen ons dat de resultaten van de examens van de eerste klas veel meer verspreid zijn dan die van de tweede klas.

De reikwijdte van klasse 1 is bijvoorbeeld veel groter:

• Klasse 1-bereik: 96 – 65 = 31
• Klasse 2-bereik: 91 – 71 = 20

De interkwartielafstand van klasse 1 is ook veel hoger:

• Klasse 1 interkwartielbereik: 90,25 – 71 = 19,25
• Klasse 2 interkwartielbereik: 84,25 – 74,75 = 9,5

De standaarddeviatie van klasse 1 is ook veel hoger:

• Standaardafwijking klasse 1: 10.21
• Standaardafwijking van klasse 2: 6,43

Elk van deze maatregelen vertelt ons dat de kloof in examenscores voor leerlingen van klas 1 veel groter is dan die voor klas 2.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende bewerkingen in Excel uitvoert:

Hoe u een samenvattende tabel in Excel maakt
Hoe de mediaan per groep in Excel te berekenen
Hoe u de standaardafwijking kunt berekenen en nul kunt negeren in Excel