Hoe u een voorspellingsinterval in excel kunt construeren

In de statistiek is eenvoudige lineaire regressie een techniek die we kunnen gebruiken om de relatie tussen een voorspellende variabele, x, en een responsvariabele, y, te kwantificeren.

Wanneer we een eenvoudige lineaire regressie uitvoeren, verkrijgen we een ‘best passende lijn’ die de relatie tussen x en y beschrijft, die kan worden geschreven als:

ŷ = _b0 + _b1 x

Goud:

• ŷ is de voorspelde waarde van de responsvariabele
• b ₀ is het y-snijpunt
• b ₁ is de regressiecoëfficiënt
• x is de waarde van de voorspellende variabele

Soms willen we deze best passende lijn gebruiken om een voorspellingsinterval te construeren voor een gegeven waarde van x ₀ , wat een interval is rond de voorspelde waarde ŷ ₀ zodat er een kans van 95% is dat de werkelijke waarde van y in de populatie overeenkomend met x ₀ is opgenomen in dit interval.

De formule voor het berekenen van het voorspellingsinterval voor een gegeven waarde x ₀ is geschreven:

ŷ ₀ +/- t _α/2,df=n-2 * se

Goud:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

De formule lijkt misschien een beetje intimiderend, maar is eigenlijk eenvoudig te berekenen in Excel. Vervolgens zien we een voorbeeld van het gebruik van deze formule om een voorspellingsinterval voor een bepaalde waarde in Excel te berekenen.

Voorbeeld: een voorspellingsinterval construeren in Excel

De volgende dataset toont het aantal gestudeerde uren en de examenscore behaald door 15 verschillende studenten:

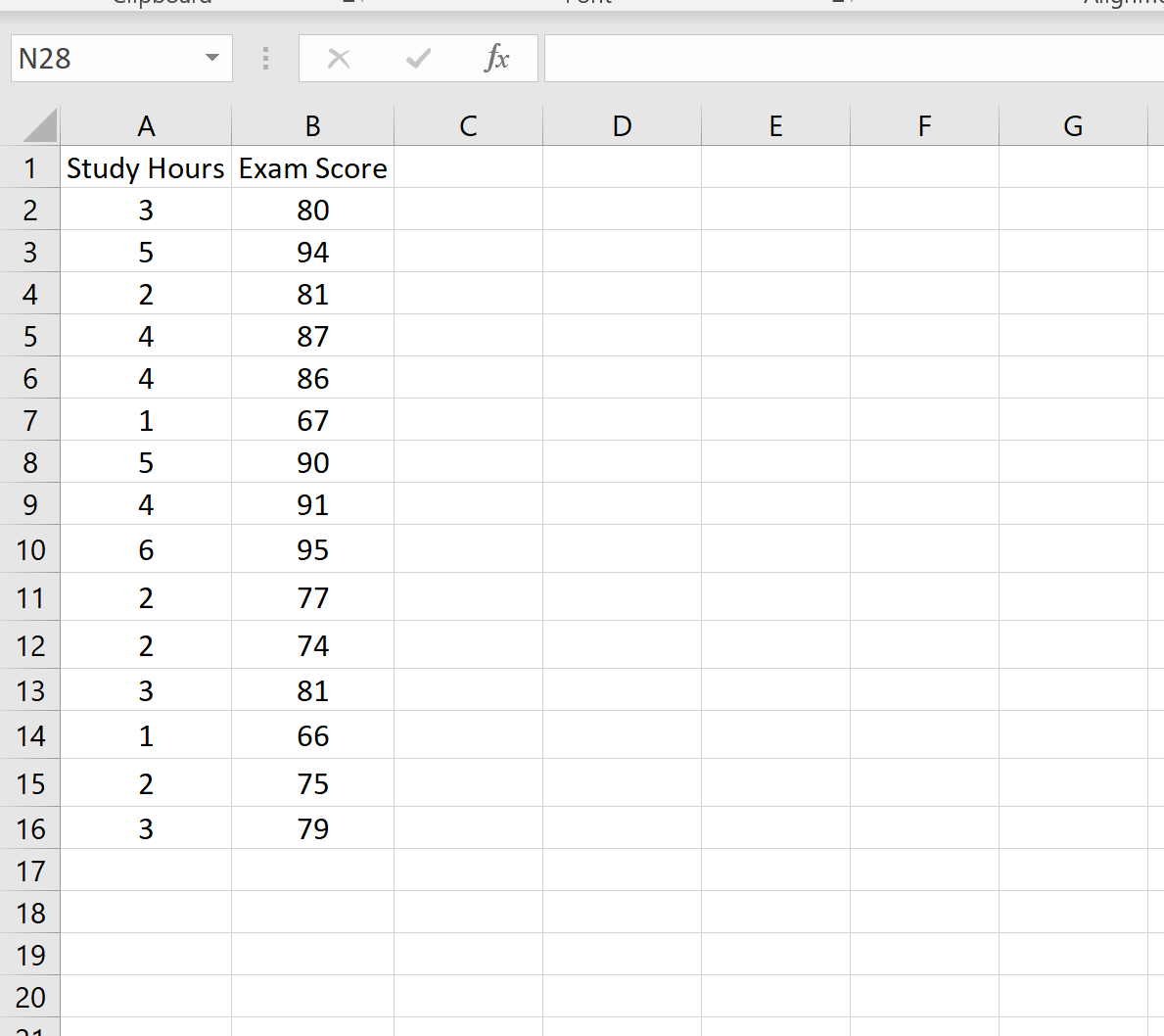
Stel dat we een voorspellingsinterval van 95% willen creëren voor de waarde x ₀ = 3. Dat wil zeggen dat we een interval willen creëren zodat er een kans van 95% is dat de examenscore binnen dit interval zal vallen voor een student die studeert voor 3 uur.

De volgende schermafbeelding laat zien hoe u alle waarden kunt berekenen die nodig zijn om dit voorspellingsinterval te verkrijgen.

Let op: De formules in kolom F laten zien hoe de waarden in kolom E zijn berekend.

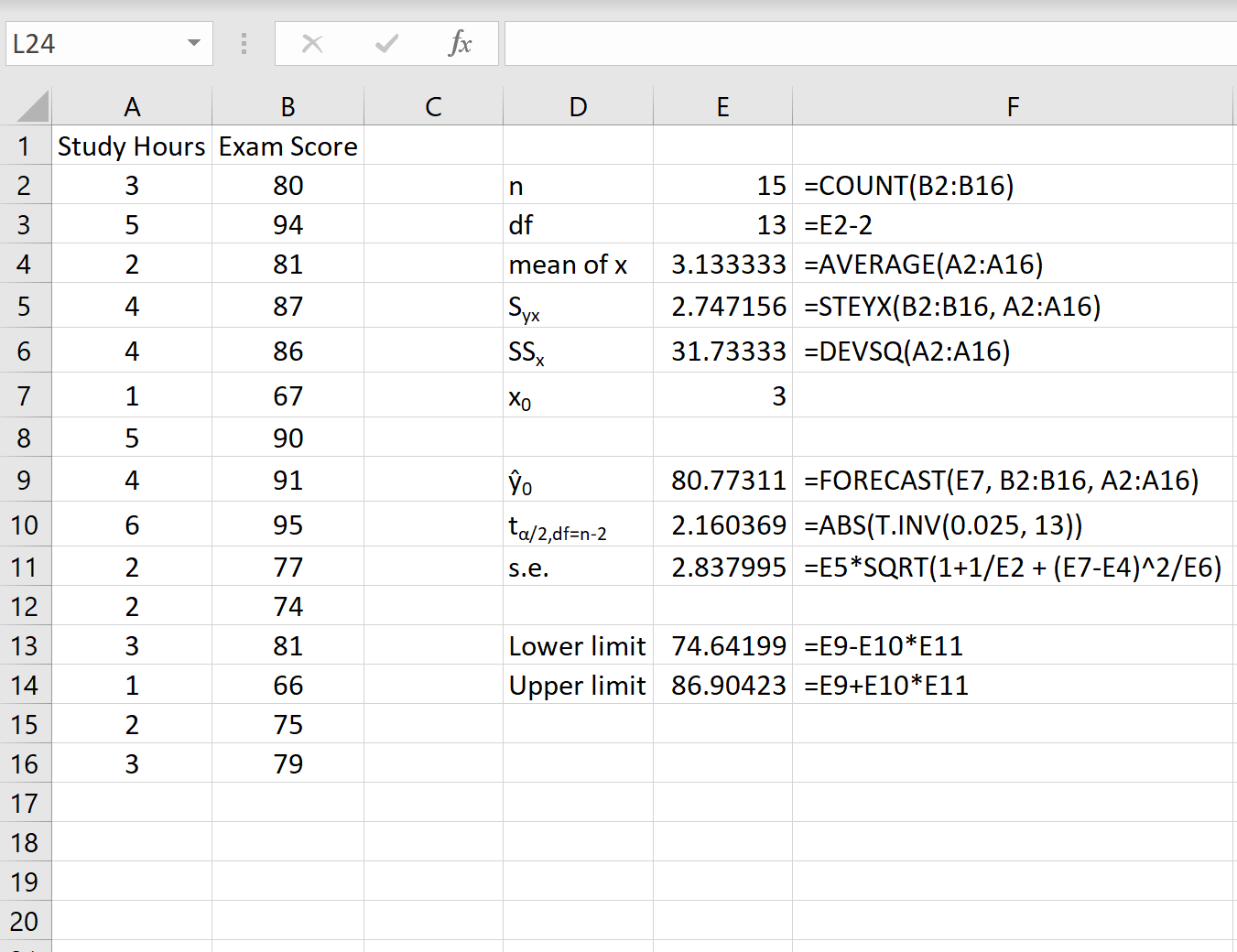
Het 95%-voorspellingsinterval voor een waarde van x ₀ = 3 is (74,64; 86,90) . Dat wil zeggen dat we met een waarschijnlijkheid van 95% voorspellen dat een student die 3 uur studeert een score tussen 74,64 en 86,90 behaalt.

Enkele opmerkingen over de gebruikte berekeningen:

• Om de t-kritische waarde van t _{α/2,df=n-2 te berekenen,} hebben we α/2 = 0,05/2 = 0,25 gebruikt, omdat we een voorspellingsinterval van 95% wilden. Merk op dat hogere voorspellingsintervallen (bijvoorbeeld een voorspellingsinterval van 99%) zullen leiden tot bredere intervallen. Omgekeerd zal een kleiner voorspellingsinterval (bijvoorbeeld een 90% voorspellingsinterval) leiden tot een smaller interval.
• We gebruikten de formule =FORECAST() om de voorspelde waarde voor ŷ ₀ te krijgen, maar de formule =FORECAST.LINEAR() retourneert exact dezelfde waarde.