Experimentele waarschijnlijkheid

Hier vindt u de betekenis van experimentele waarschijnlijkheid en hoe experimentele waarschijnlijkheid wordt berekend. Bovendien kunt u een stapsgewijs opgelost voorbeeld bekijken van het berekenen van de experimentele waarschijnlijkheid.

Wat is experimentele waarschijnlijkheid?

Experimentele waarschijnlijkheid is een statistische maatstaf gebaseerd op de resultaten van een experiment of empirische feiten en geeft de waarschijnlijkheid aan dat een gebeurtenis plaatsvindt.

Bovendien geldt dat hoe vaker het experiment wordt herhaald, des te nauwkeuriger de verkregen experimentele waarschijnlijkheid zal zijn. Om deze reden worden over het algemeen computerprogramma’s gebruikt die in staat zijn om snel duizenden experimenten te simuleren om de experimentele waarschijnlijkheid te bepalen, waardoor een betere nauwkeurigheid wordt verkregen.

Experimentele waarschijnlijkheid wordt ook wel empirische waarschijnlijkheid of frequentiewaarschijnlijkheid genoemd.

Experimentele waarschijnlijkheid is een getal tussen 0 en 1. Logisch gezien geldt: hoe groter de waarde van de experimentele waarschijnlijkheid van een gebeurtenis, hoe waarschijnlijker het is dat deze zal plaatsvinden, en omgekeerd: hoe kleiner de waarde, hoe kleiner de kans dat deze zal plaatsvinden. waarschijnlijk zal optreden. of de gebeurtenis plaatsvindt. Maar de waarde van de experimentele waarschijnlijkheid zal altijd tussen nul en één liggen.

Experimentele waarschijnlijkheidsformule

De formule voor experimentele waarschijnlijkheid is het aantal keren dat een gebeurtenis plaatsvond tijdens een experiment gedeeld door het totale aantal keren dat het experiment werd uitgevoerd.

Als een persoon bijvoorbeeld tien pijlen naar een doel gooit en erin slaagt zes pijlen in het midden te raken, wordt de kans dat die persoon een pijl in het midden raakt als volgt berekend:

Voorbeeld van experimentele waarschijnlijkheid

Zodra we de wiskundige definitie van experimentele waarschijnlijkheid hebben gezien, zullen we een stapsgewijze oefening met dit soort waarschijnlijkheid oplossen. Het doel is dat u leert hoe de experimentele waarschijnlijkheid van een gebeurtenis wordt berekend. Als u dus vragen heeft, kunt u deze in de opmerkingen stellen.

• Bereken de experimentele waarschijnlijkheid van de elementaire gebeurtenissen waaruit het willekeurige experiment van het gooien van een dobbelsteen bestaat.

Voordat we de experimentele waarschijnlijkheid vinden, zullen we de theoretische waarschijnlijkheid berekenen om de verkregen experimentele resultaten te vergelijken met de theoretische resultaten. Zoals u wel weet, zijn er zes mogelijke uitkomsten bij het gooien van een dobbelsteen (1, 2, 3, 4, 5 en 6), dus de theoretische waarschijnlijkheid van elke elementaire gebeurtenis is:

Om deze oefening op te lossen, moeten we simuleren dat we meerdere keren met een dobbelsteen gooien en de resultaten in een kruistabel vastleggen. In dit geval doen wij de simulaties met het programma Excel, maar u kunt uiteraard ook het programma van uw keuze gebruiken.

We zullen eerst tien worpen simuleren, dan honderd worpen en ten slotte duizend worpen. Op deze manier kunnen we de resultaten analyseren en zien hoe ze veranderen afhankelijk van de steekproefomvang van het experiment. De resultaten verkregen na willekeurige simulatie van 10 dobbelsteenworpen zijn als volgt:

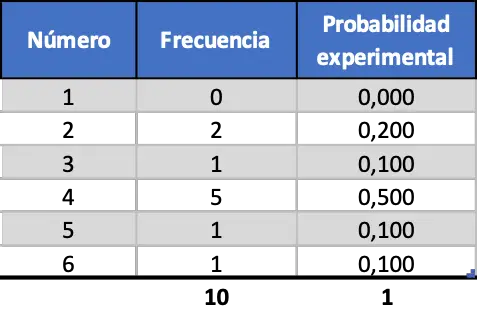
Zoals u kunt zien, zijn de verkregen experimentele kansen momenteel behoorlijk verschillend van de eerder berekende theoretische kansen (0,167).

Maar naarmate we het aantal tests vergroten, gaan deze twee statistieken steeds meer op elkaar lijken. Kijk eens naar de simulatie van 100 lanceringen:

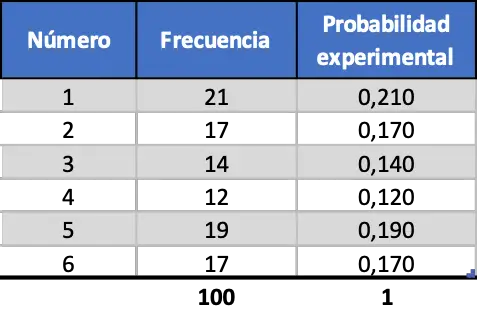
Nu lijkt de experimentele waarschijnlijkheid meer op de theoretische waarschijnlijkheidswaarde, maar we krijgen nog steeds verre waarden.

Ten slotte voeren we dezelfde procedure uit, maar simuleren we 1000 lanceringen:

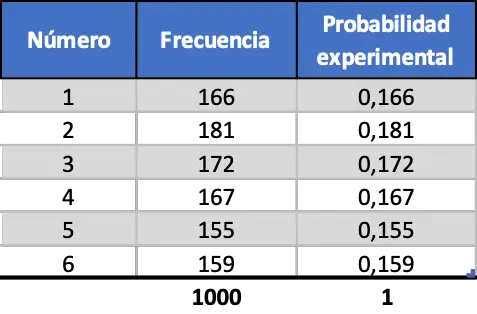
Zoals je in de laatste contingentietabel kunt zien, lijken de waarden van de experimentele kansen nu sterk op de theoretische kansen.

Samenvattend: hoe groter het aantal uitgevoerde experimenten, hoe dichter de waarde van de experimentele waarschijnlijkheid van een gebeurtenis zal liggen bij de theoretische waarschijnlijkheid ervan . Deze regel wordt gedefinieerd als de wet van de grote getallen , die stelt dat hoe meer gegevens er zijn, hoe dichter de experimentele waarden bij de theoretische waarden zullen liggen.

Op dezelfde manier zul je, als je de drie frequentietabellen vergelijkt, zien dat de experimentele waarschijnlijkheid niet definitief is, maar evolueert afhankelijk van het aantal uitgevoerde experimenten. Dat betekent dat je moet weten hoe je de verkregen waarden moet interpreteren.

Experimentele waarschijnlijkheid en theoretische waarschijnlijkheid

Het verschil tussen experimentele waarschijnlijkheid en theoretische waarschijnlijkheid (of klassieke waarschijnlijkheid) is dat experimentele waarschijnlijkheid wordt berekend op basis van gegevens verzameld uit een echt experiment, terwijl theoretische waarschijnlijkheid wordt berekend zonder dat het nodig is om een experiment uit te voeren.

Zoals we hebben gezien moeten we een groot aantal experimenten simuleren om de experimentele waarschijnlijkheid van een gebeurtenis af te leiden. Het berekenen van de theoretische waarschijnlijkheid heeft echter betrekking op theorie en logica. Je kunt hier zien hoe het moet: