Hoe exponentiële distributie in excel te gebruiken

De exponentiële verdeling is een waarschijnlijkheidsverdeling die wordt gebruikt om de tijd te modelleren die we moeten wachten totdat een bepaalde gebeurtenis plaatsvindt.

Deze verdeling kan worden gebruikt om vragen te beantwoorden zoals:

• Hoe lang moet een detailhandelaar wachten tot een klant zijn winkel binnenkomt?
• Hoe lang blijft een batterij werken voordat deze leeg raakt?
• Hoe lang zal een computer blijven werken voordat hij kapot gaat?

Bij elk scenario willen we berekenen hoe lang we moeten wachten tot een bepaalde gebeurtenis plaatsvindt. Elk scenario kan dus worden gemodelleerd met behulp van een exponentiële verdeling.

Als een willekeurige variabele X een exponentiële verdeling volgt, kan de cumulatieve dichtheidsfunctie van X worden geschreven:

F (x; λ) = 1 – e ^-λx

Goud:

• λ: de snelheidsparameter (berekend als λ = 1/μ)
• e: Een constante die ongeveer gelijk is aan 2,718

Om de kansen te berekenen die verband houden met de cumulatieve dichtheidsfunctie van de exponentiële verdeling in Excel, kunnen we de volgende formule gebruiken:

 =EXPON.DIST(x, lambda, cumulative)

Goud:

• x : de waarde van de exponentieel verdeelde willekeurige variabele
• lambda : de snelheidsparameter
• cumulatief : of de cumulatieve dichtheidsfunctie wel of niet moet worden gebruikt (TRUE of FALSE)

De volgende voorbeelden laten zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld 1: tijd tot de volgende klant arriveert

Gemiddeld komt er elke twee minuten een nieuwe klant een winkel binnen. Nadat een klant arriveert, bepaalt u de kans dat er binnen een minuut een nieuwe klant arriveert.

Oplossing: De gemiddelde tijd tussen klanten bedraagt twee minuten. Het tarief kan dus als volgt worden berekend:

• λ = 1/μ
• λ = 1/2
• λ = 0,5

We kunnen dus de volgende formule in Excel gebruiken om de kans te berekenen dat er binnen een minuut een nieuwe klant arriveert:

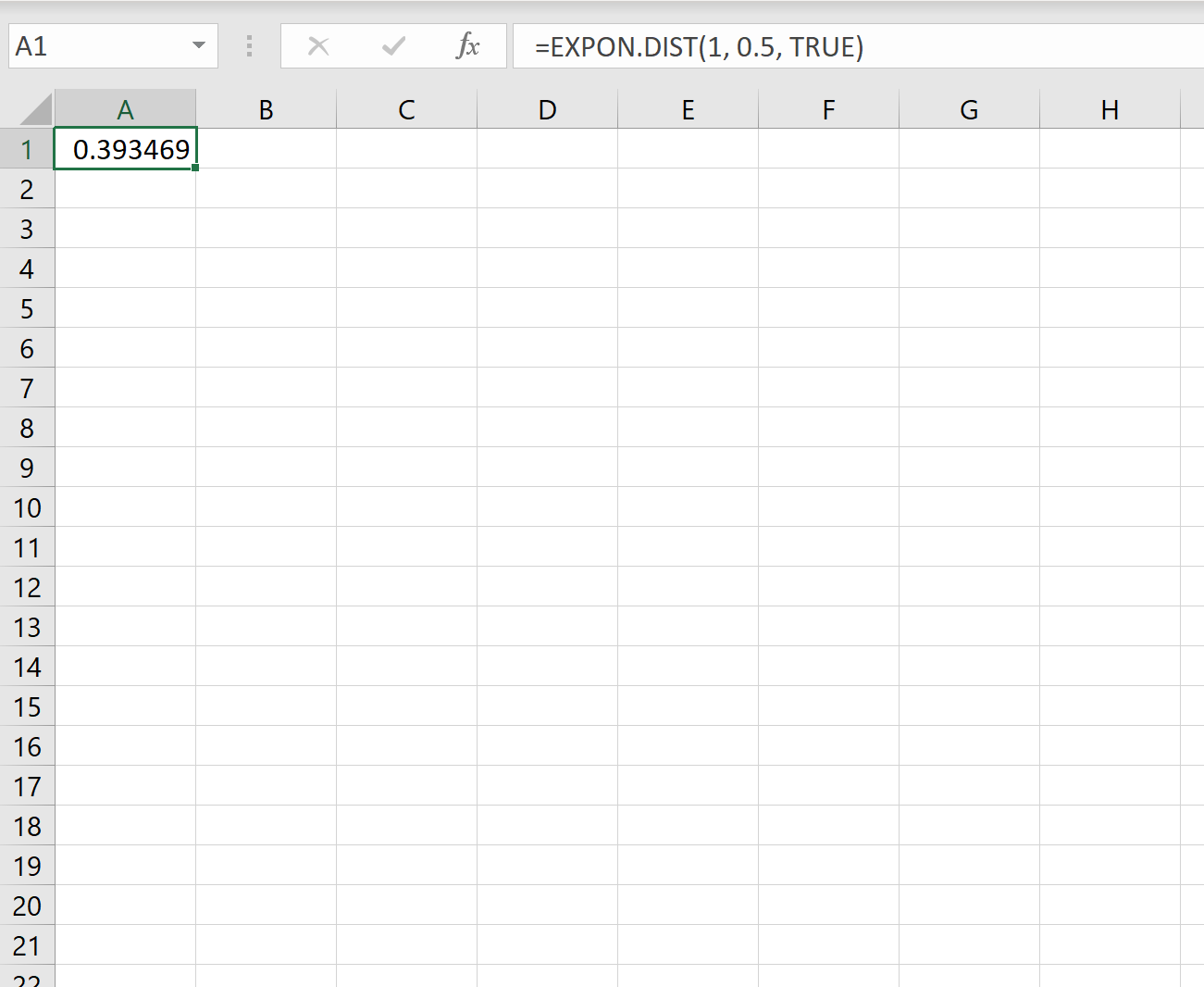
De kans dat we minder dan een minuut moeten wachten op de volgende klant is 0,393469 .

Voorbeeld 2: Tijd tot de volgende aardbeving

Stel dat er in een bepaalde regio gemiddeld elke 400 dagen een aardbeving plaatsvindt. Bepaal na een aardbeving de kans dat het meer dan 500 dagen duurt voordat de volgende aardbeving plaatsvindt.

Oplossing: De gemiddelde tijd tussen aardbevingen is 400 dagen. Het tarief kan dus als volgt worden berekend:

• λ = 1/μ
• λ = 1/400
• λ = 0,0025

We kunnen dus de volgende formule in Excel gebruiken om de kans te berekenen dat de volgende aardbeving minder dan 500 dagen zal duren:

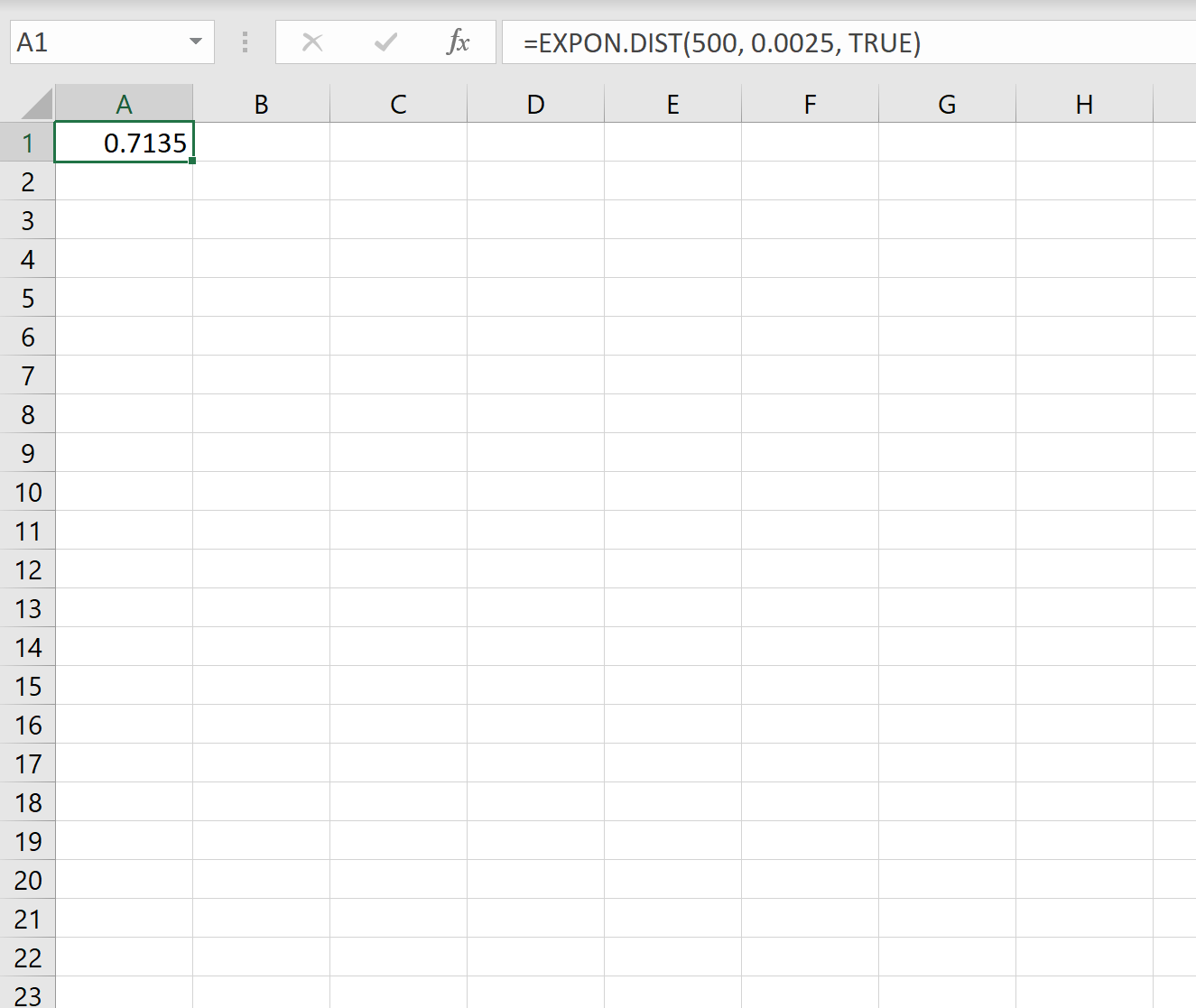
De kans dat het minder dan 500 dagen duurt voordat de volgende aardbeving plaatsvindt, is 0,7135.

De kans dat we meer dan 500 dagen moeten wachten op de volgende aardbeving is dus 1 – 0,7135 = 0,2865 .

Voorbeeld 3: Tijd tot het volgende telefoongesprek

Laten we zeggen dat een callcenter gemiddeld elke 10 minuten een nieuwe oproep ontvangt. Nadat een klant belt, bepaal je de kans dat een nieuwe klant binnen 10 tot 15 minuten belt.

Oplossing: De gemiddelde tijd tussen oproepen bedraagt 10 minuten. Het tarief kan dus als volgt worden berekend:

• λ = 1/μ
• λ = 1/10
• λ = 0,1

We kunnen dus de volgende formule in Excel gebruiken om de kans te berekenen dat de volgende klant binnen 10 tot 15 minuten belt:

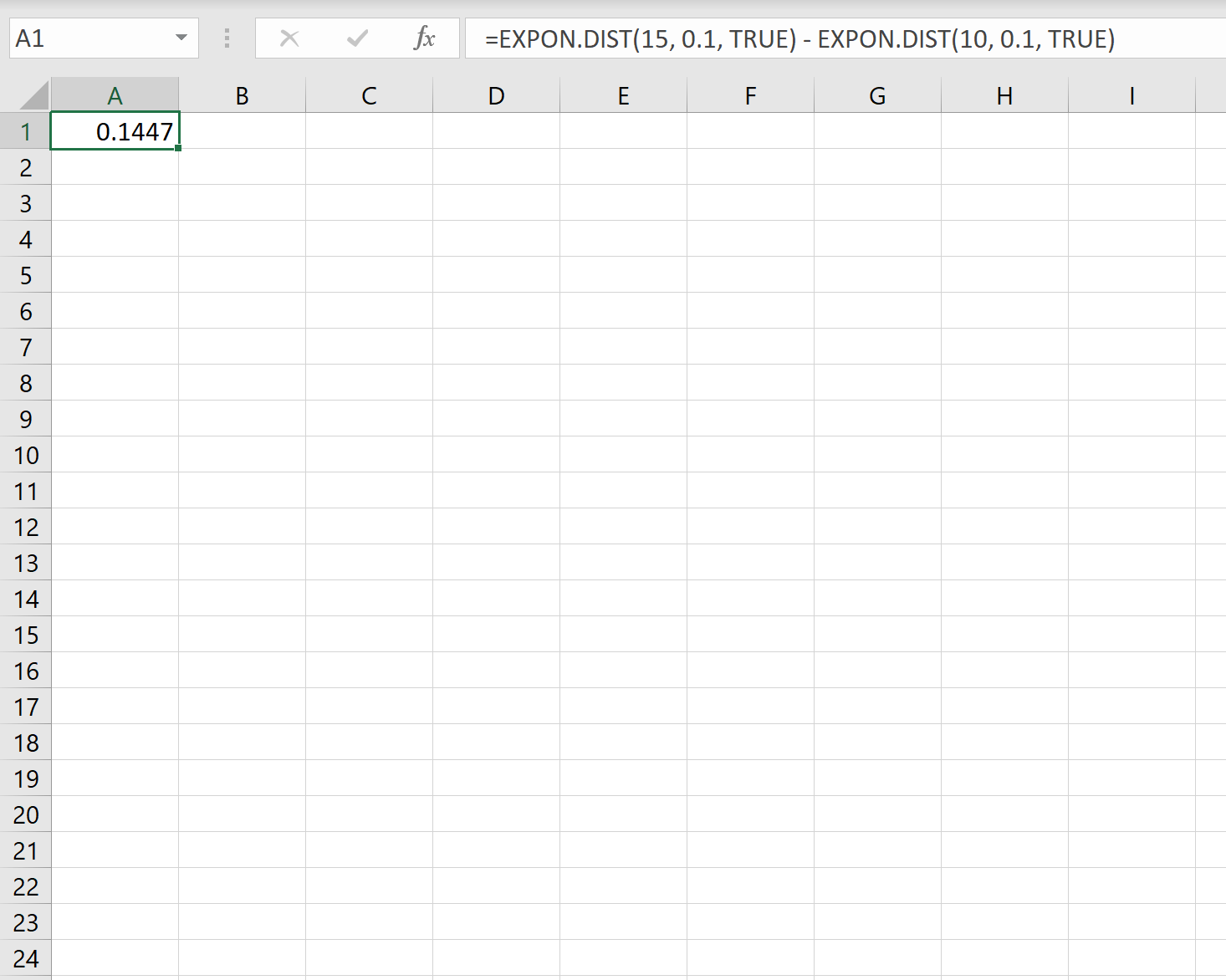
De kans dat een nieuwe klant binnen 10-15 minuten belt. bedraagt 0,1447 .

Aanvullende bronnen

Een inleiding tot de exponentiële verdeling
De geheugenloze eigenschap van de exponentiële verdeling
Hoe een exponentiële verdeling in R te plotten