Hoe exponentiële distributie in python te gebruiken

De exponentiële verdeling is een waarschijnlijkheidsverdeling die wordt gebruikt om de tijd te modelleren die we moeten wachten totdat een bepaalde gebeurtenis plaatsvindt.

Als een willekeurige variabele X een exponentiële verdeling volgt, kan de cumulatieve verdelingsfunctie van X worden geschreven:

F (x; λ) = 1 – e ^-λx

Goud:

• λ: de snelheidsparameter (berekend als λ = 1/μ)
• e: Een constante die ongeveer gelijk is aan 2,718

In deze tutorial wordt uitgelegd hoe u de exponentiële distributie in Python gebruikt.

Hoe een exponentiële verdeling te genereren

U kunt de functie expon.rvs(scale, size) uit de SciPy-bibliotheek in Python gebruiken om willekeurige waarden te genereren uit een exponentiële verdeling met een specifieke snelheidsparameter en steekproefomvang:

 from scipy. stats import expo

#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )

array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
        34.60922432, 2.68266663, 22.70459831, 97.66661811,
         6.64272914, 46.15547298])

Opmerking : u kunt de volledige SciPy-bibliotheekdocumentatie hier vinden.

Hoe kansen te berekenen met behulp van een exponentiële verdeling

Stel dat het gemiddelde aantal minuten tussen uitbarstingen van een bepaalde geiser 40 minuten bedraagt. Hoe waarschijnlijk is het dat we minder dan 50 minuten zullen moeten wachten op een uitbarsting?

Om dit probleem op te lossen, moeten we eerst de tariefparameter berekenen:

• λ = 1/μ
• λ = 1/40
• λ = 0,025

We kunnen λ = 0,025 en x = 50 in de CDF-formule pluggen:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

De kans dat we minder dan 50 minuten zullen moeten wachten op de volgende uitbarsting is 0,7135 .

We kunnen de functie expon.cdf() van SciPy gebruiken om dit probleem in Python op te lossen:

 from scipy. stats import expo

#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)

0.7134952031398099

De kans dat we minder dan 50 minuten zullen moeten wachten op de volgende uitbarsting is 0,7135 .

Dit komt overeen met de waarde die we handmatig hebben berekend.

Hoe een exponentiële verdeling te plotten

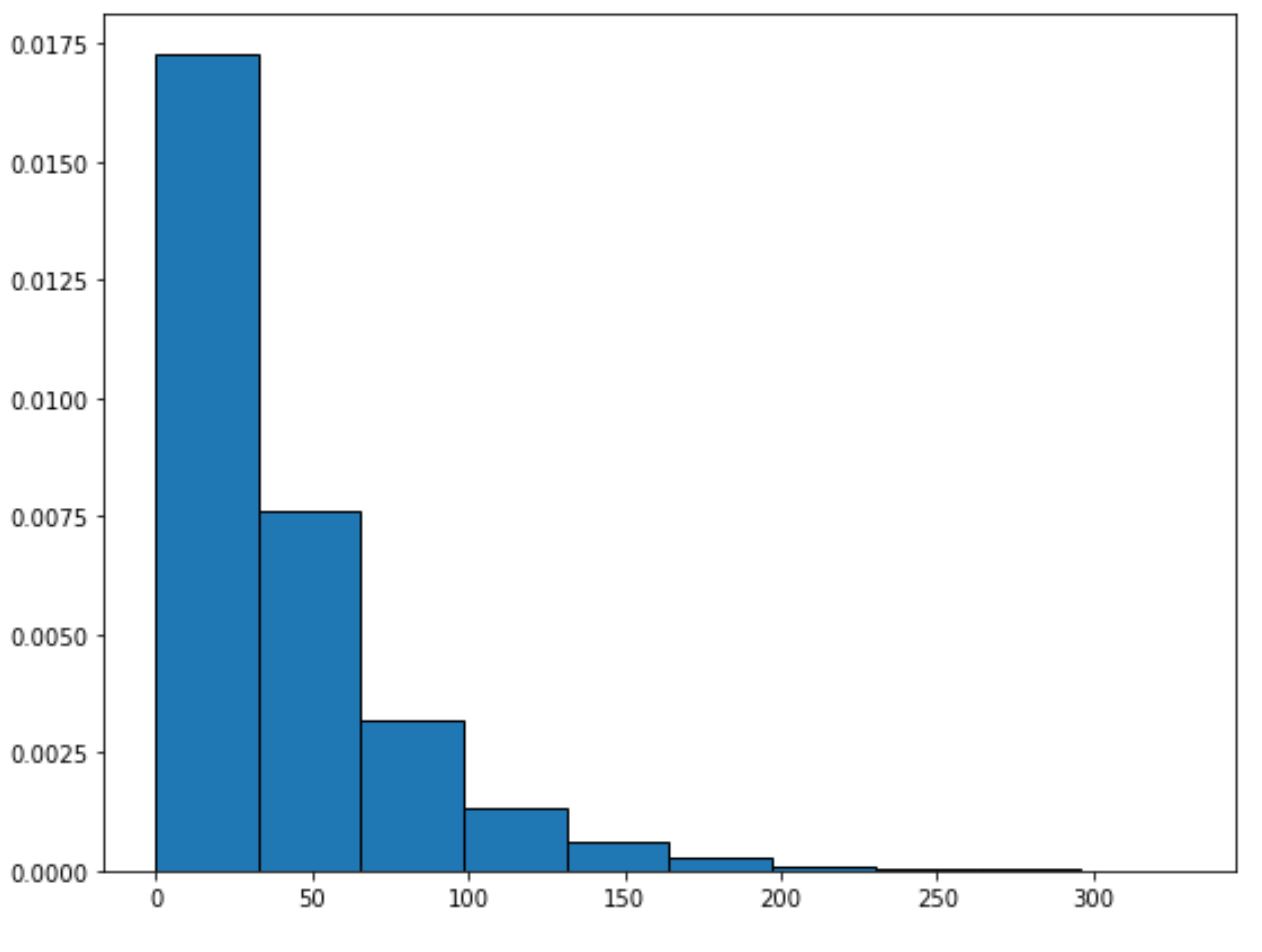
U kunt de volgende syntaxis gebruiken om een exponentiële verdeling uit te zetten met een bepaalde tariefparameter:

 from scipy. stats import expo
import matplotlib. pyplot as plt

#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 ,size= 10000 )

#create plot of exponential distribution
plt. hist (x, density= True , edgecolor=' black ')

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelgebruikte distributies in Python kunt gebruiken:

Hoe de Poisson-distributie in Python te gebruiken
Hoe t-distributie in Python te gebruiken
Hoe uniforme distributie in Python te gebruiken