Exponentiële regressie in r (stap voor stap)

Exponentiële regressie is een type regressie dat kan worden gebruikt om de volgende situaties te modelleren:

1. Exponentiële groei: De groei begint langzaam en versnelt vervolgens snel en zonder beperking.

2. Exponentieel verval: Het verval begint snel en vertraagt vervolgens om steeds dichter bij nul te komen.

De vergelijking voor een exponentieel regressiemodel heeft de volgende vorm:

y = ^abx

Goud:

• y: de responsvariabele
• x: de voorspellende variabele
• a, b: de regressiecoëfficiënten die de relatie tussen x en y beschrijven

Het volgende stapsgewijze voorbeeld laat zien hoe u exponentiële regressie in R kunt uitvoeren.

Stap 1: Creëer de gegevens

Laten we eerst valse gegevens maken voor twee variabelen: x en y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Stap 2: Visualiseer de gegevens

Laten we vervolgens een snelle spreidingsdiagram maken om de relatie tussen x en y te visualiseren:

 plot(x, y) 

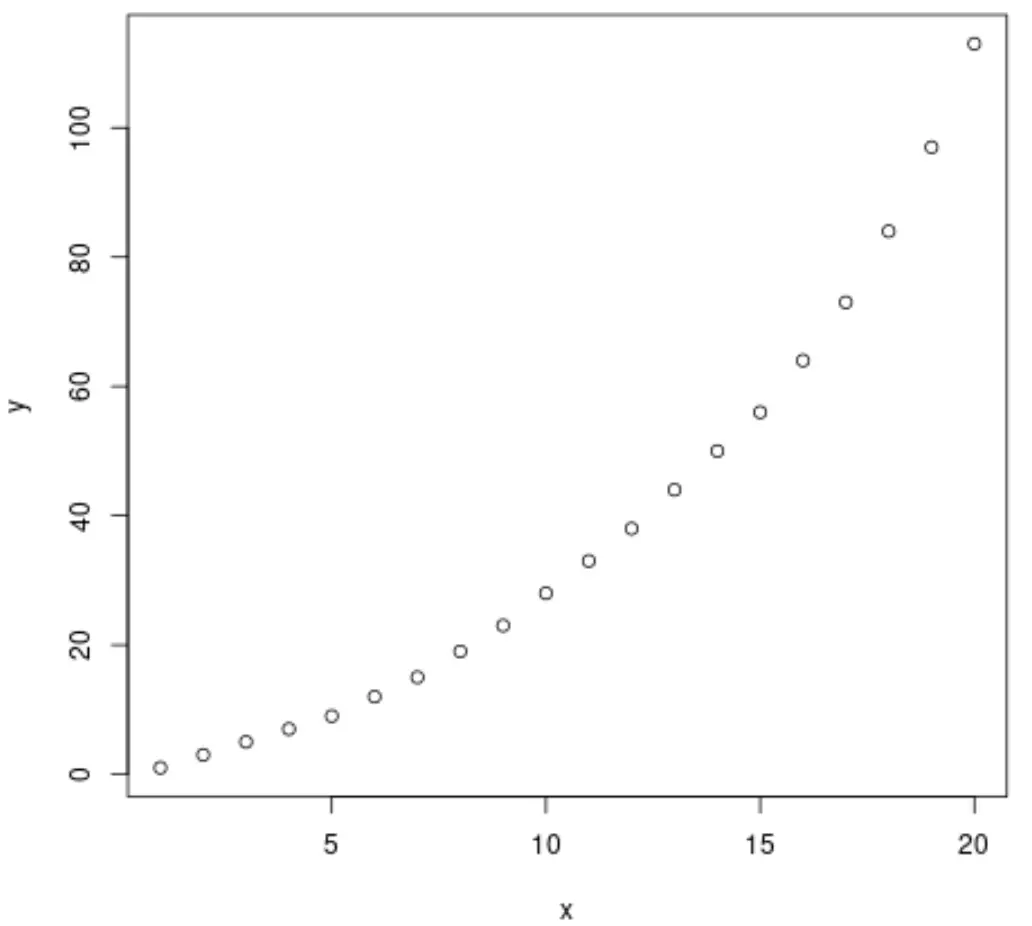
Uit de grafiek kunnen we zien dat er een duidelijk exponentieel groeipatroon bestaat tussen de twee variabelen.

Het lijkt daarom verstandig om een exponentiële regressievergelijking toe te passen om de relatie tussen de variabelen te beschrijven.

Stap 3: Pas het exponentiële regressiemodel toe

Vervolgens zullen we de functie lm() gebruiken om een exponentieel regressiemodel te fitten, waarbij we de natuurlijke logaritme van y alsde responsvariabele en x als de voorspellende variabele gebruiken:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

De totale F-waarde van het model is 204 en de overeenkomstige p-waarde is extreem laag (2.917e-11), wat aangeeft dat het model als geheel bruikbaar is.

Met behulp van de coëfficiënten uit de uitvoertabel kunnen we zien dat de aangepaste exponentiële regressievergelijking is:

ln(y) = 0,9817 + 0,2041(x)

Door e op beide zijden toe te passen, kunnen we de vergelijking als volgt herschrijven:

y = 2,6689 * ^1,2264x

We kunnen deze vergelijking gebruiken om de responsvariabele, y , te voorspellen op basis van de waarde van de voorspellende variabele, x . Als x = 12, dan voorspellen we bijvoorbeeld dat y 30,897 zou zijn:

j = 2,6689 * 1,2264 ¹² = 30,897

Bonus: voel je vrij om deze online exponentiële regressiecalculator te gebruiken om automatisch de exponentiële regressievergelijking voor een bepaalde voorspeller en responsvariabele te berekenen.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe kwadratische regressie uit te voeren in R
Hoe polynomiale regressie uit te voeren in R