Exponentiële verdeling

In dit artikel wordt uitgelegd wat de exponentiële verdeling in de statistiek is en waarvoor deze wordt gebruikt. Op dezelfde manier zul je ontdekken wat de eigenschappen zijn van de exponentiële verdeling, evenals de formules, de grafiek en een opgeloste oefening. Bovendien kunt u elke waarschijnlijkheid berekenen met een online exponentiële verdelingscalculator.

Wat is exponentiële verdeling?

De exponentiële verdeling is een continue kansverdeling die wordt gebruikt om de wachttijd voor het optreden van een willekeurig fenomeen te modelleren.

Preciezer gezegd, de exponentiële verdeling stelt ons in staat de wachttijd te beschrijven tussen twee gebeurtenissen die een Poisson-verdeling volgt. Daarom is de exponentiële verdeling nauw verwant aan de Poisson-verdeling.

De exponentiële verdeling heeft een karakteristieke parameter, weergegeven door de Griekse letter λ, en geeft aan hoe vaak de bestudeerde gebeurtenis naar verwachting zal plaatsvinden gedurende een bepaalde tijdsperiode.

Op dezelfde manier wordt de exponentiële verdeling ook gebruikt om de tijd te modelleren totdat er een storing optreedt. De exponentiële verdeling heeft daarom verschillende toepassingen in de betrouwbaarheids- en overlevingstheorie.

Voorbeelden van exponentiële verdelingen

Nu we de definitie van exponentiële verdeling kennen, gaan we naar verschillende voorbeelden van dit type verdeling kijken om het concept beter te begrijpen.

Voorbeelden van exponentiële verdeling:

1. De tijd die verstrijkt tussen twee oproepen in een callcenter.
2. De tijd die iemand moet wachten tot er een gratis taxi in een bepaalde straat passeert.
3. De wachttijd totdat een nieuwe klant een winkel binnenkomt.
4. De tijd die verstrijkt tussen twee verschillende gebruikers die een webpagina bezoeken.
5. De tijd die op een luchthaven verstrijkt tussen het opstijgen van het ene vliegtuig en het vertrek van een ander vliegtuig.

Exponentiële verdelingsformule

De dichtheidsfunctieformule die de berekening van een exponentiële verdelingswaarschijnlijkheid definieert, is gelijk aan λ vermenigvuldigd met het getal e tot de macht van negatief λ maal x.

Met andere woorden, de formule voor het berekenen van een exponentiële verdelingskans is als volgt:

👉 U kunt de onderstaande rekenmachine gebruiken om de waarschijnlijkheid te berekenen van een variabele die de exponentiële verdeling volgt.

Aan de andere kant is de formule om een cumulatieve waarschijnlijkheid van de exponentiële verdeling te berekenen als volgt:

Exponentiële verdelingsgrafiek

In deze sectie ziet u de grafische weergave van de dichtheidsfunctie en de verdelingsfunctie van exponentiële verdeling.

Hieronder kunt u zien hoe de grafiek van de dichtheidsfunctie van de exponentiële verdeling varieert afhankelijk van de waarde van de parameter λ.

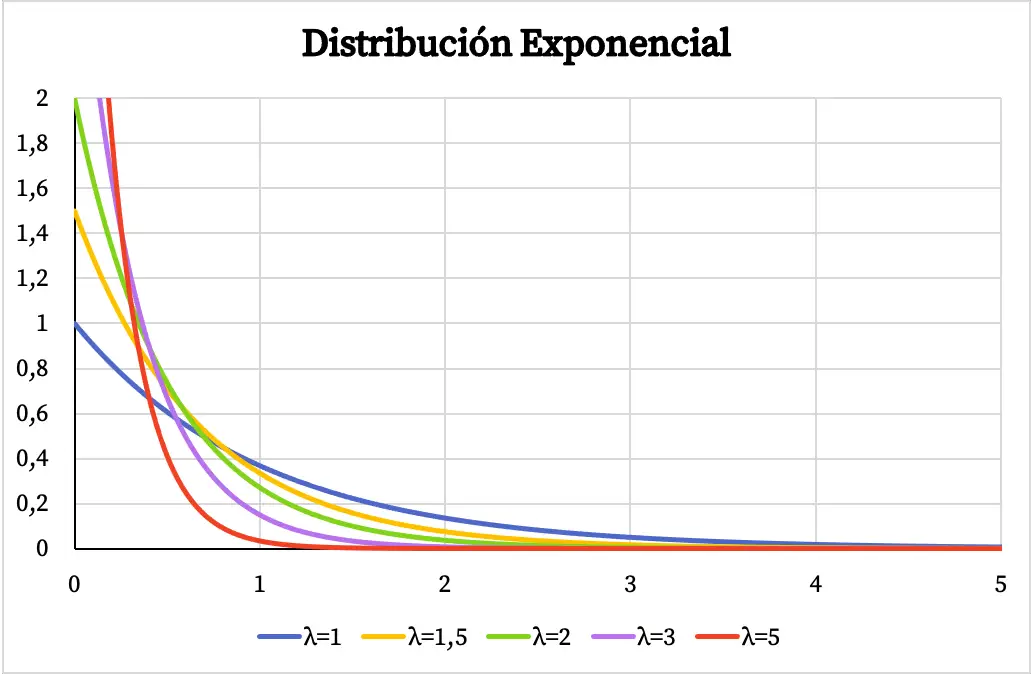
Op dezelfde manier hangt de cumulatieve waarschijnlijkheidsfunctie van de exponentiële verdeling ook af van de waarde van de parameter λ, zoals u kunt zien in de volgende grafiek:

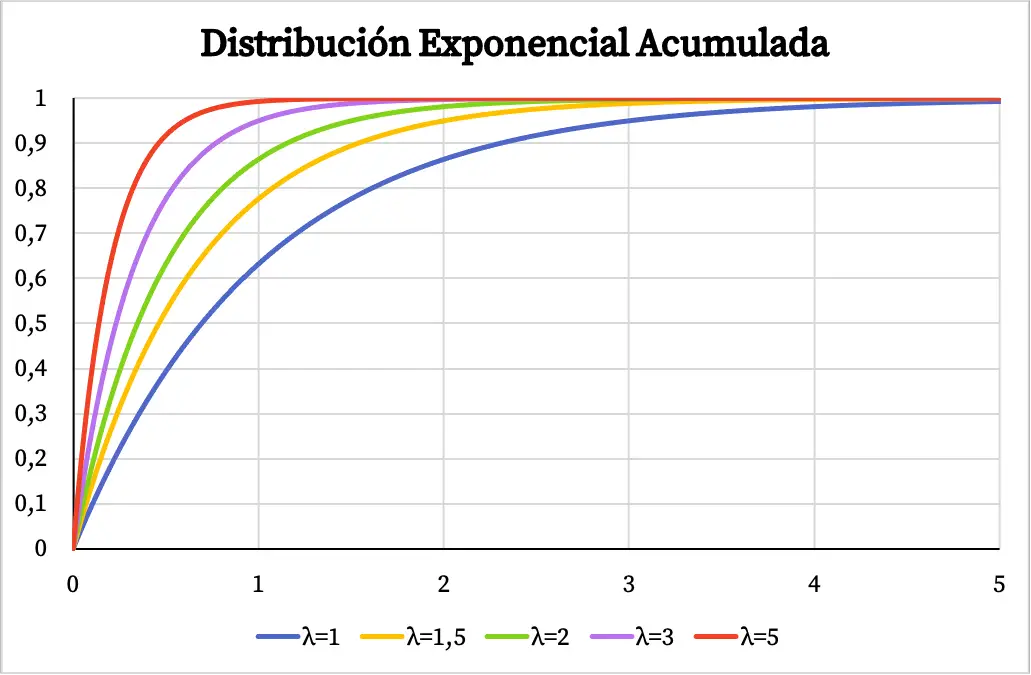
Opgeloste oefening over exponentiële verdeling

• Gemiddeld hebben λ=1 gebruikers/min toegang tot een specifieke webpagina. Wat is de kans dat de tijd tussen twee binnenkomende gebruikers drie minuten bedraagt? En de kans dat deze gelijk is aan of kleiner is dan 2 minuten?

De verdeling die de willekeurige variabele van dit probleem definieert, is een exponentiële verdeling, omdat we de tijd bestuderen die verstrijkt vanaf het moment dat een gebeurtenis plaatsvindt (de toegang van een gebruiker op de webpagina) totdat dezelfde gebeurtenis opnieuw plaatsvindt.

Om de waarschijnlijkheid te berekenen dat de tijd die verstrijkt tussen de invoer van twee verschillende gebruikers drie minuten bedraagt, moeten we daarom de formule voor de dichtheidsfunctie toepassen (zie hierboven):

Aan de andere kant moeten we, om een cumulatieve waarschijnlijkheid te bepalen, de verdelingsfunctieformule van de exponentiële verdeling gebruiken:

Kenmerken van de exponentiële verdeling

De exponentiële verdeling heeft de volgende kenmerken:

• De exponentiële verdeling heeft een karakteristieke parameter, λ, die aangeeft hoe vaak het bestudeerde fenomeen naar verwachting zal optreden gedurende een bepaalde tijdsperiode.

• De exponentiële verdeling kan geen negatieve waarde aannemen, dus het domein van de exponentiële verdeling bestaat uit alle reële getallen groter dan of gelijk aan nul.

• Het gemiddelde van de exponentiële verdeling is gelijk aan één gedeeld door de karakteristieke parameter λ.

• De variantie van de exponentiële verdeling is het kwadraat van het gemiddelde, daarom is de variantie van de exponentiële verdeling gelijk aan één over de coëfficiënt λ in het kwadraat.

• Wat de waarde van λ ook is, de asymmetriecoëfficiënt van de exponentiële verdeling is altijd gelijk aan 2.

• Op dezelfde manier is de kurtosis-coëfficiënt van elke exponentiële verdeling altijd gelijk aan 9.

• De formule voor de dichtheidsfunctie van de exponentiële verdeling is:

• Terwijl de formule voor de cumulatieve waarschijnlijkheidsfunctie van de exponentiële verdeling als volgt is:

• De exponentiële verdeling is een van de weinige kansverdelingen met de eigenschap dat er geen geheugen meer is. Deze eigenschap houdt in dat het optreden van een eerdere gebeurtenis geen invloed heeft op de waarschijnlijkheid dat die gebeurtenis zich in de toekomst zal voordoen. Bij een exponentiële verdeling hangt de waarschijnlijkheid dat een nieuwe gebruiker binnen een minuut een webpagina bezoekt bijvoorbeeld niet af van het feit of een gebruiker net is binnengekomen of dat er sindsdien geen gebruiker meer is geweest. ruim tien minuten.

Exponentiële verdelingscalculator

Voer de waarde van de parameter λ en de waarde van x in de volgende rekenmachine in om de waarschijnlijkheid te berekenen. U moet de waarschijnlijkheid selecteren die u wilt berekenen en de getallen invoeren met de punt als decimaal scheidingsteken, bijvoorbeeld 0,50.