Hoe residuen uit de lm()-functie in r te extraheren

U kunt de volgende syntaxis gebruiken om residuen uit de functie lm() in R te extraheren:

 fit$residuals

In dit voorbeeld wordt ervan uitgegaan dat we de functie lm() hebben gebruikt om een lineair regressiemodel te fitten en de resultaten fit hebben genoemd.

Het volgende voorbeeld laat zien hoe u deze syntaxis in de praktijk kunt gebruiken.

Gerelateerd: Hoe de R-kwadraat uit de functie lm() in R te extraheren

Voorbeeld: Hoe residuen uit lm() in R te extraheren

Stel dat we het volgende dataframe in R hebben dat informatie bevat over de gespeelde minuten, het totaal aantal fouten en het totaal aantal punten gescoord door 10 basketbalspelers:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

Stel dat we willen passen in het volgende meervoudige lineaire regressiemodel:

punten = β ₀ + β ₁ (minuten) + β ₂ (overtredingen)

We kunnen de functie lm() gebruiken om in dit regressiemodel te passen:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

We kunnen dan fit$residuals typen om de residuen uit het model te extraheren:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

Omdat er in totaal 10 waarnemingen in onze database zaten, zijn er 10 residuen – één voor elke waarneming.

Bijvoorbeeld:

• De eerste waarneming heeft een residu van 2.089 .
• De tweede waarneming heeft een residu van -0,798 .
• De derde waarneming heeft een residu van 0,637 .

Enzovoort.

We kunnen dan een grafiek maken van de residuen tegen de aangepaste waarden als we dat willen:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

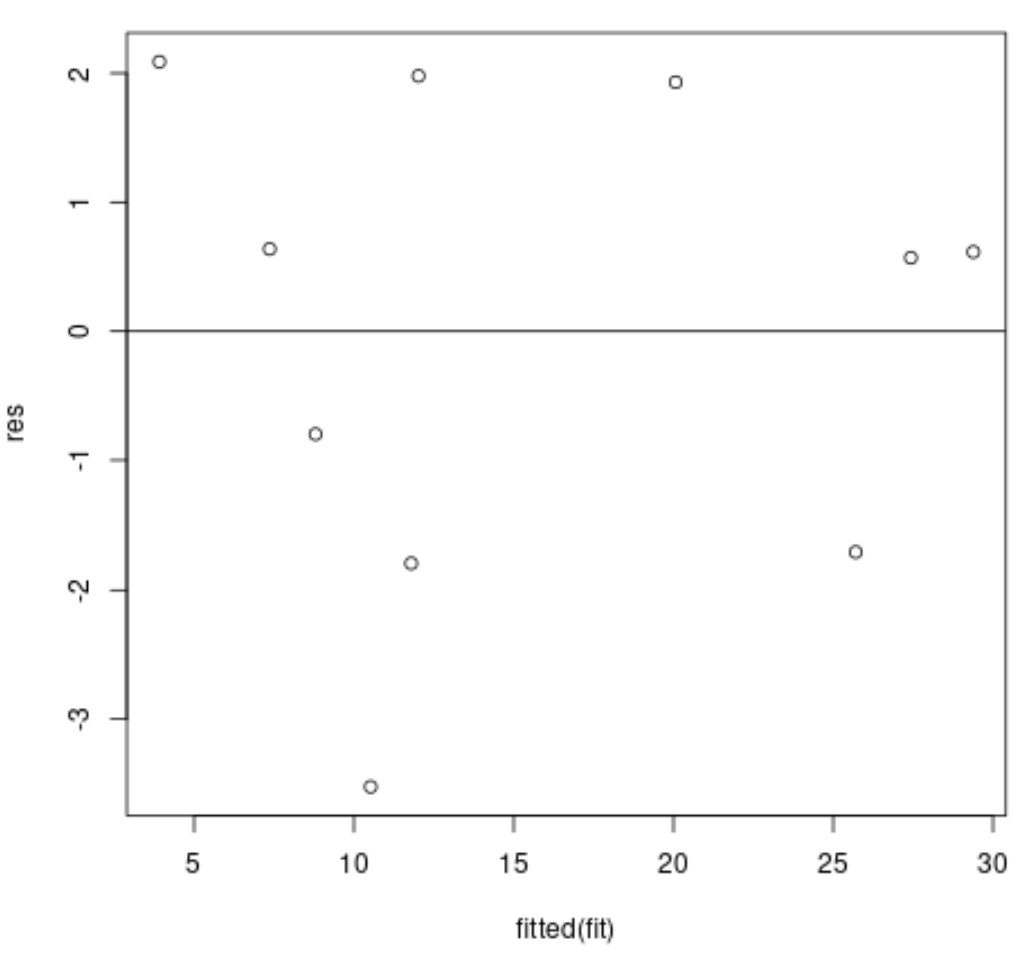
Op de x-as worden de gefitte waarden weergegeven en op de y-as de residuen.

Idealiter zouden de residuen willekeurig rond nul verspreid moeten zijn, zonder duidelijk patroon, om ervoor te zorgen dat aan de aanname van homoscedasticiteit wordt voldaan.

In de bovenstaande grafiek van de residuen kunnen we zien dat de residuen willekeurig rond nul verspreid lijken te zijn, zonder duidelijk patroon, wat betekent dat waarschijnlijk aan de aanname van homoscedasticiteit is voldaan.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe maak je een restplot in R