Hoe fitdistr() in r te gebruiken om distributies te passen

U kunt de functie fitdistr() uit het MASS- pakket in R gebruiken om de parameters van een verdeling te schatten door de waarschijnlijkheidsfunctie te maximaliseren.

Deze functie gebruikt de volgende basissyntaxis:

fitdistr(x, compactfun, …)

Goud:

• x : Een numerieke vector die de waarden van de verdeling vertegenwoordigt
• densityfun : de verdeling waarvoor de parameters moeten worden geschat

Merk op dat het densityfun- argument de volgende potentiële distributienamen accepteert: beta , cauchy , chi-kwadraat , exponentieel , gamma , geometrisch , lognormaal , logistiek , negatief binomiaal , normaal , Poisson , t en Weibull .

Het volgende voorbeeld laat zien hoe u de functie fitdistr() in de praktijk kunt gebruiken.

Voorbeeld: hoe u de functie fitdistr() gebruikt om verdelingen in R passend te maken

Stel dat we de functie rnorm() in R gebruiken om een vector van 200 waarden te genereren die een normale verdeling volgt:

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

We kunnen de functie hist() gebruiken om een histogram te maken om de verdeling van gegevenswaarden te visualiseren:

 hist(data, col=' steelblue ')

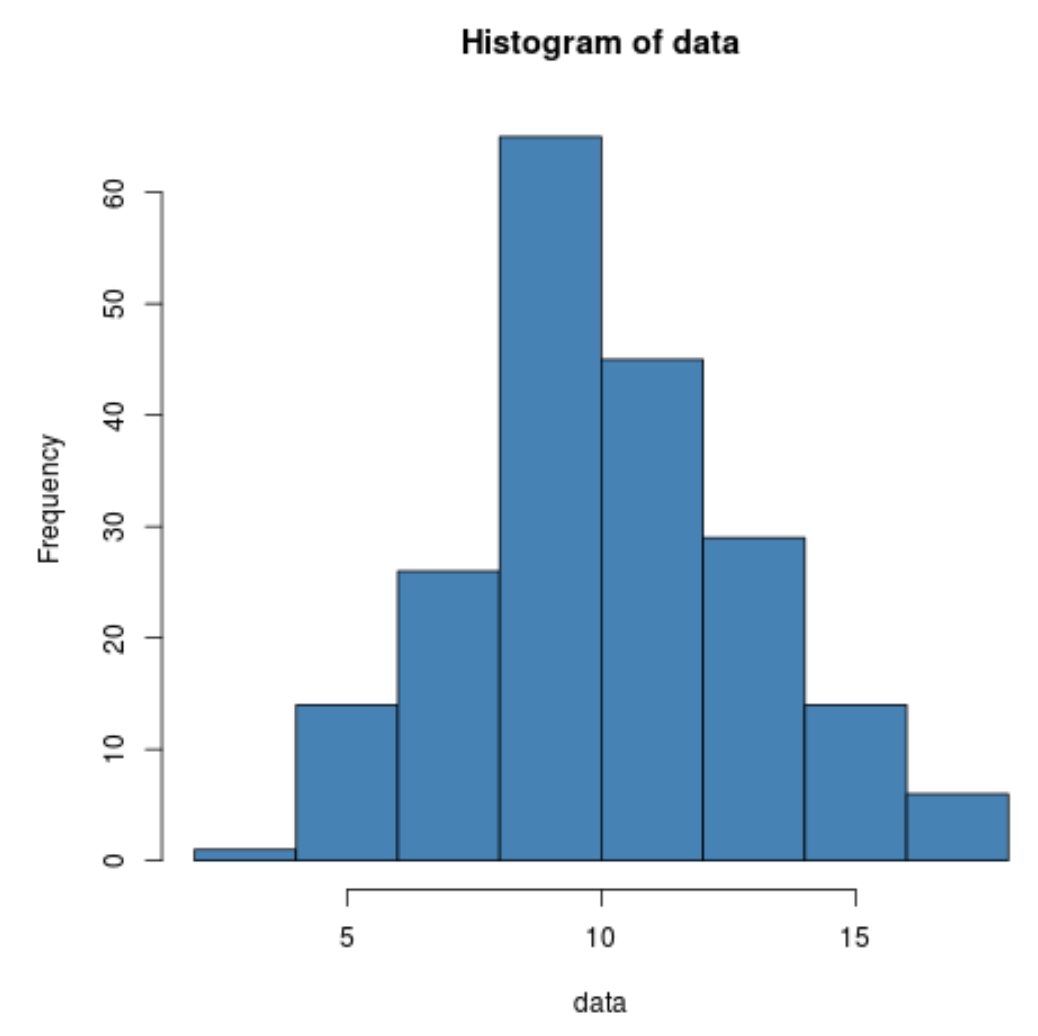
We kunnen zien dat de gegevens inderdaad normaal verdeeld lijken.

We kunnen dan de functie fitdistr() gebruiken om de parameters van deze verdeling te schatten:

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

De functie fitdistr() schat dat de vector van waarden een normale verdeling volgt met een gemiddelde van 10,1066189 en een standaardafwijking van 2,7803148 .

Deze waarden hoeven niet verrassend te zijn, aangezien we de gegevens hebben gegenereerd met behulp van de functie rnorm() met een gemiddelde waarde van 10 en een standaardafwijking van 3.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe een normale verdeling in R te plotten
Hoe een normale verdeling in R te genereren
Hoe een Shapiro-Wilk-test uit te voeren voor normaliteit in R