Frequentieverdeling
In dit artikel wordt uitgelegd wat frequentieverdelingen zijn en hoe ze worden bereikt. Ook vind je stap-voor-stap voorbeelden van frequentieverdelingen en daarnaast kun je oefenen met opgeloste oefeningen.
Wat is een frequentieverdeling?
In de statistieken is de frequentieverdeling een tabel waarin de verschillende waarden van een monster in rijen zijn gegroepeerd en in elke kolom wordt van elke waarde een frequentietype weergegeven. Daarom wordt frequentieverdeling gebruikt om alle soorten frequenties in een dataset weer te geven.
Meer specifiek omvat een frequentieverdeling absolute frequentie, cumulatieve absolute frequentie, relatieve frequentie en cumulatieve relatieve frequentie.
Een van de kenmerken van frequentieverdelingen is dat ze zeer nuttig zijn voor het samenvatten van een statistische steekproef van een kwantitatieve variabele en een kwalitatieve variabele.
Hoe maak je een frequentieverdeling?
Om een frequentieverdeling uit te voeren, moet u de volgende stappen volgen:
- Organiseer de gegevens in verschillende categorieën en maak een tabel waarin elke rij overeenkomt met een categorie.
- Bereken de absolute frequentie van elke categorie in de tweede kolom van de tabel.
- Bereken de cumulatieve absolute frequentie van elke categorie in de derde kolom van de tabel.
- Bereken de relatieve frequentie van elke categorie in de vierde kolom van de tabel.
- Bereken de cumulatieve relatieve frequentie van elke categorie in de vijfde kolom van de tabel.
- Optioneel kunnen twee kolommen worden toegevoegd waarin de relatieve frequentie en de cumulatieve relatieve frequentie als percentage worden berekend, hiervoor hoeft u beide kolommen eenvoudigweg met 100 te vermenigvuldigen.
Voorbeeld van frequentieverdeling
Nadat we de definitie van frequentieverdeling en de theorie over hoe deze is opgebouwd hebben gezien, wordt in deze sectie een voorbeeld stap voor stap opgelost.
- De cijfers behaald voor het vak statistiek in een klas van 30 studenten zijn als volgt. Construeer een frequentieverdeling van de dataset.
![]()
![]()
![]()
Omdat alle getallen alleen gehele getallen kunnen zijn, is het een discrete variabele. Het is daarom niet nodig om de gegevens in intervallen te groeperen.
Om een frequentieverdeling te maken, moeten we dus een tabel construeren waarin elke verschillende waarde een rij zal zijn, en dan moeten we de absolute frequentie van elke waarde vinden:

Merk op dat de som van alle absolute frequenties gelijk is aan het totale aantal gegevens. Indien deze regel niet gerespecteerd wordt, betekent dit dat u vergeten bent bepaalde gegevens te verstrekken.
Nu we de absolute frequentie kennen, moeten we de cumulatieve absolute frequentie berekenen. Voor deze berekening hebben we twee opties: ofwel voegen we de absolute frequentie van de waarde toe plus alle absolute frequenties van de kleinste waarden, ofwel voegen we de absolute frequentie van de waarde toe plus de cumulatieve absolute frequentie van de vorige waarde.

De cumulatieve absolute frequentie van de laatste waarde komt altijd overeen met het totale aantal gegevens. U kunt deze truc gebruiken om te verifiëren dat de berekeningen correct zijn.
Vervolgens moeten we de relatieve frequentie bepalen, die wordt berekend door de absolute frequentie te delen door het totale aantal datapunten (30):

Houd er rekening mee dat de som van alle relatieve frequenties altijd gelijk is aan 1, anders betekent dit dat een bepaalde berekening van de frequentieverdeling verkeerd is.
Ten slotte hoeven we alleen maar de cumulatieve relatieve frequentie te extraheren. Om dit te doen, moet u de relatieve frequentie van de betreffende waarde optellen plus alle voorgaande relatieve frequenties of, wat op hetzelfde neerkomt, de vorige geaccumuleerde relatieve frequentie:

Kort gezegd is de frequentieverdeling met alle frequenties van de probleemgegevens als volgt:

Frequentieverdeling voor gegroepeerde gegevens
Om een frequentieverdeling te maken voor gegevens die in intervallen zijn gegroepeerd , is het enige verschil dat de gegevensset eerst in verschillende intervallen moet worden gegroepeerd, maar de rest van de berekeningen wordt op dezelfde manier uitgevoerd als bij een frequentieverdeling zonder de gegevens te groeperen.
Als voorbeeld wordt hieronder een probleem opgelost van het construeren van een frequentieverdeling voor gegroepeerde gegevens.
- De lengte van 20 personen werd gemeten en de onderstaande resultaten werden verkregen. Creëer een frequentieverdeling door de gegevens in intervallen te verdelen.
![]()
![]()
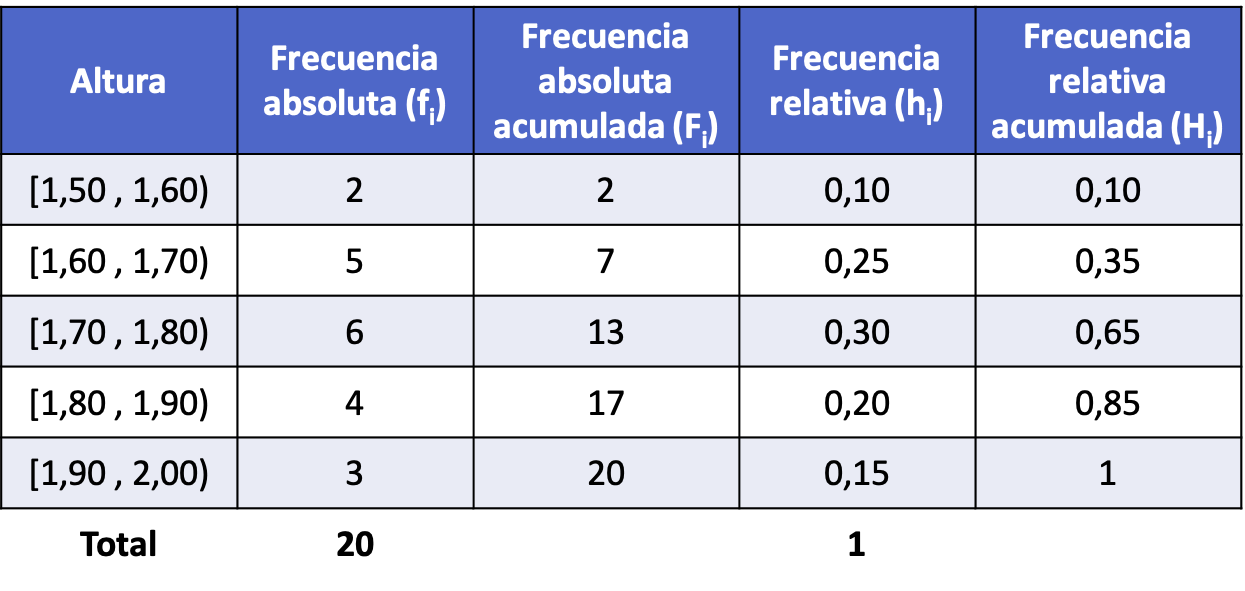
De gegevens in dit voorbeeld volgen een continue verdeling, omdat de getallen decimaal kunnen zijn en daarom elke waarde kunnen aannemen. Daarom zullen we de frequentieverdeling maken door de gegevens in intervallen te groeperen.
Hoewel er verschillende wiskundige regels zijn voor het maken van de intervallen van een sample, maken we in dit geval eenvoudigweg intervallen met een breedte van 10 tienden.
Dus na het berekenen van alle frequentietypen voor elk interval (de procedure is hetzelfde als in het bovenstaande voorbeeld), is de frequentieverdeling met de gegevens gegroepeerd in intervallen als volgt:
Frequentieverdelingsoefeningen opgelost
Oefening 1
We vroegen 20 mensen hoe vaak ze per maand naar de bioscoop gaan en hier zijn de resultaten:
![]()
![]()
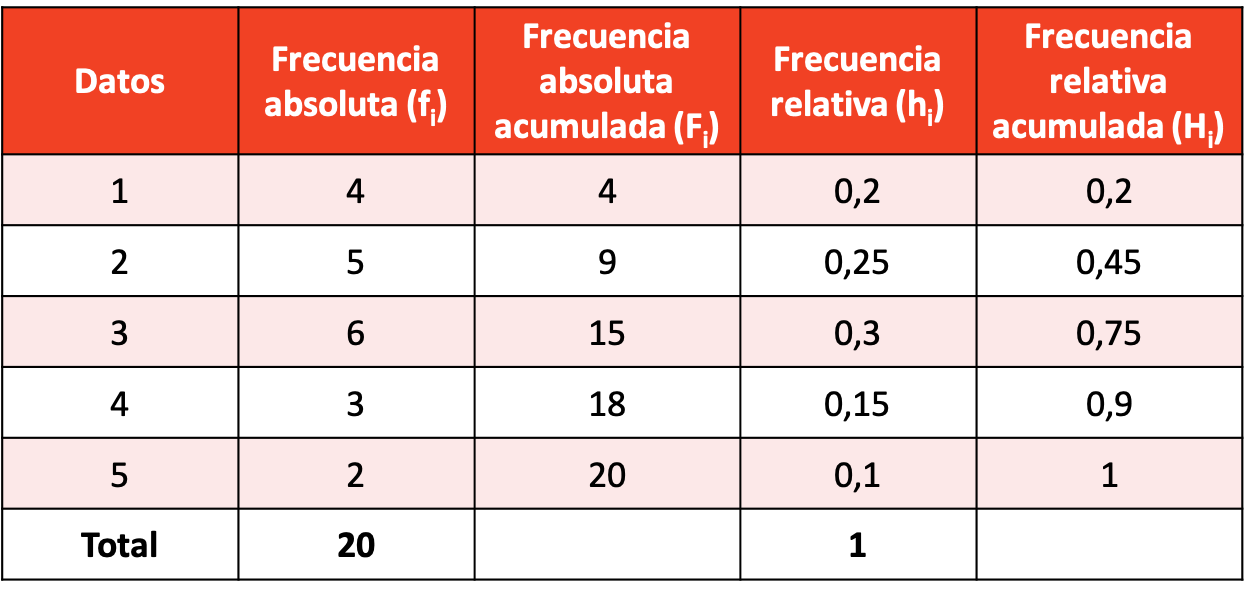
Maak een frequentieverdeling met het resulterende gegevensmonster.
De frequentieverdeling met berekeningen van alle soorten frequenties is als volgt:
Oefening 2
U wilt een statistisch onderzoek uitvoeren naar het gewicht van de werknemers in een bedrijf met 36 werknemers. Hier zijn de gewichten van de arbeiders, uitgedrukt in kilogram:
![]()
![]()
![]()
![]()
![]()
![]()
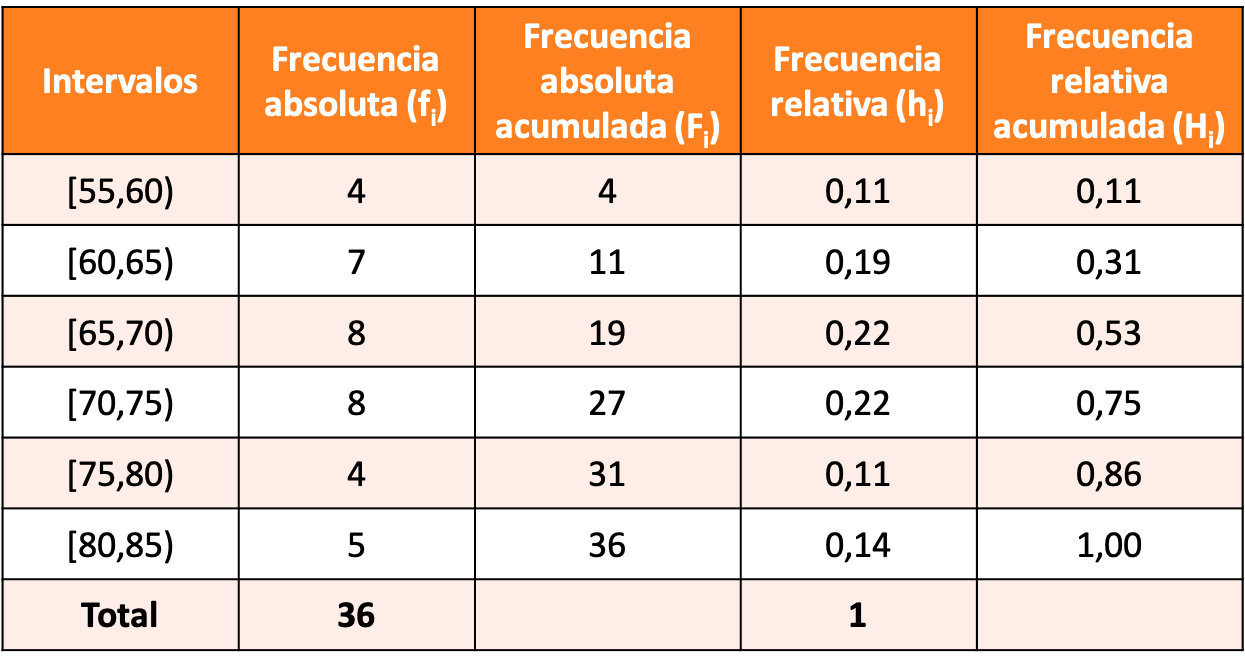
Construeer een frequentieverdeling met gegroepeerde gegevens door intervallen van 5 eenheden te maken en laat het eerste interval [55,60) zijn.
De oplossing voor de oefening is de volgende frequentieverdeling: