Friedman-test: definitie, formule en voorbeeld

De Friedman-test is een niet-parametrisch alternatief voor ANOVA met herhaalde metingen .

Het wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer groepen waarin dezelfde onderwerpen in elke groep voorkomen.

Wanneer moet u de Friedman-test gebruiken?

De Friedman-test wordt vaak in twee situaties gebruikt:

1. Meet de gemiddelde scores van proefpersonen over drie of meer tijdstippen.

U wilt bijvoorbeeld de resterende hartslag van de proefpersonen meten één maand voordat u met een trainingsprogramma begint, één maand na het starten van het programma en twee maanden na gebruik van het programma. U kunt de Friedman-test uitvoeren om te zien of er op deze drie tijdstippen een significant verschil is in de gemiddelde resterende hartslag van de patiënt.

2. Meet de gemiddelde scores van proefpersonen in drie verschillende omstandigheden.

U kunt de proefpersonen bijvoorbeeld vragen om drie verschillende films te bekijken en elke film te beoordelen op basis van hoe leuk ze deze vonden. Omdat elk onderwerp in elk voorbeeld voorkomt, kun je een Friedman-test uitvoeren om te zien of er een significant verschil is in de gemiddelde beoordeling van de drie films.

Friedman-test: voorbeeld

Stel dat we willen weten of de gemiddelde reactietijd van proefpersonen verschillend is op drie verschillende medicijnen. Om dit te testen, rekruteren we 10 patiënten en meten we elk van hun reactietijden (in seconden) op de drie verschillende medicijnen. De resultaten voor elke patiënt worden hieronder weergegeven:

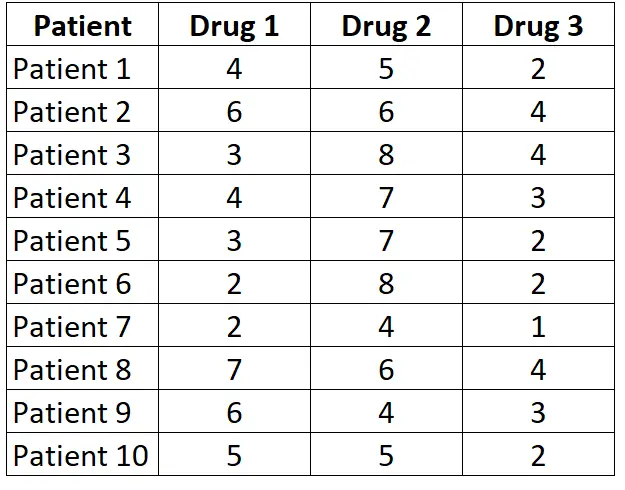
Omdat bij elke patiënt elk van de drie medicijnen wordt gemeten, zullen we de Friedman-test gebruiken om te bepalen of de gemiddelde reactietijd tussen de drie medicijnen verschilt.

Stap 1. Formuleer de hypothesen.

De nulhypothese (H ₀ ): µ ₁ = µ ₂ = µ ₃ (gemiddelde reactietijden over populaties zijn allemaal gelijk)

De alternatieve hypothese: (Ha): ten minste één populatiegemiddelde verschilt van de rest

Stap 2. Voer de Friedman-test uit.

We zullen de Friedman-testcalculator gebruiken met behulp van de volgende invoer:

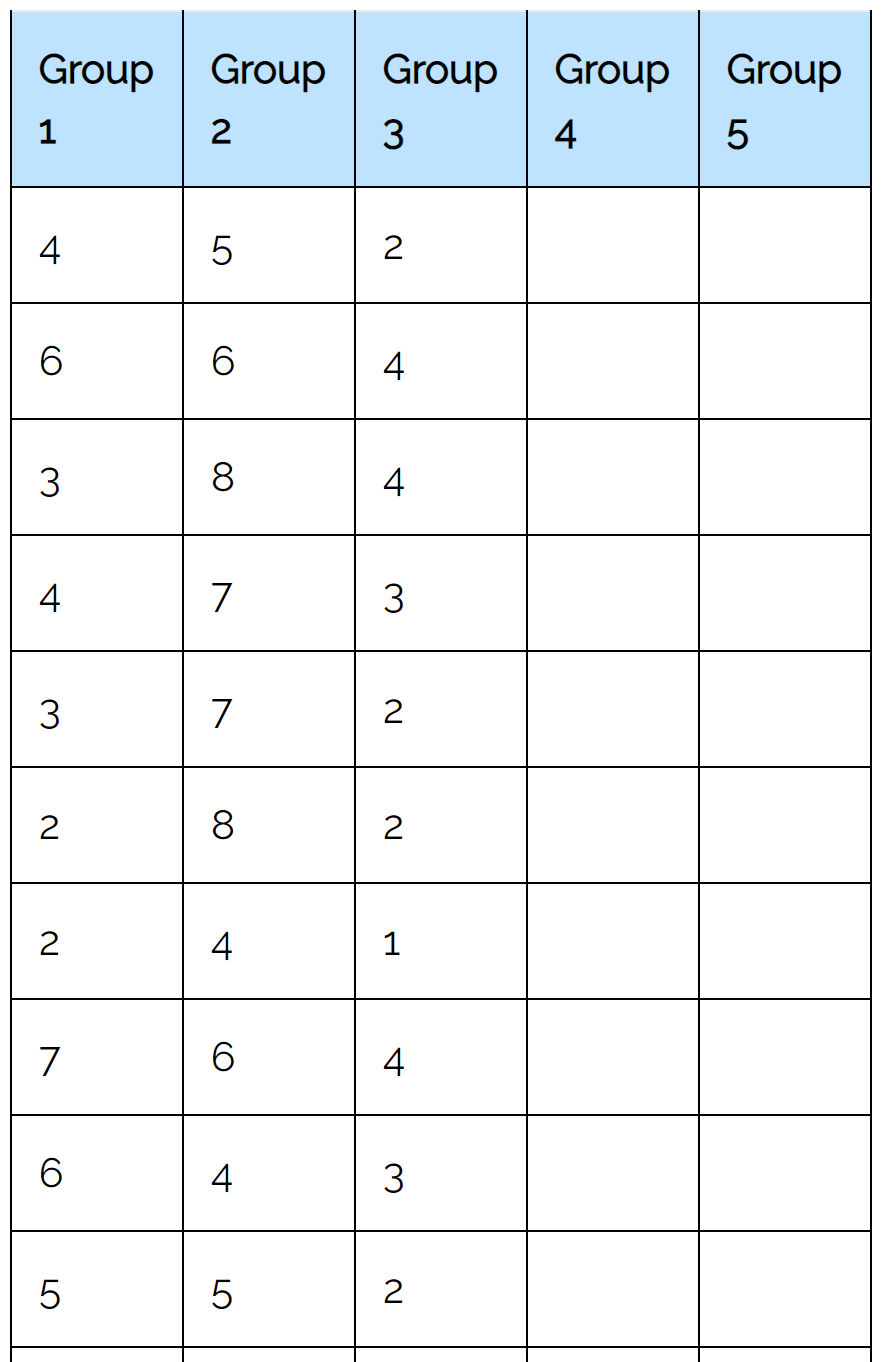
Zodra we op “Berekenen” klikken, verschijnt automatisch het volgende resultaat:

Stap 3: Interpreteer de resultaten.

De teststatistiek is Q = 12,35 en de overeenkomstige p-waarde is p = 0,00208 . Omdat deze waarde kleiner is dan 0,05, kunnen we de nulhypothese verwerpen dat de gemiddelde responstijd voor alle drie de geneesmiddelen hetzelfde is.

We hebben voldoende bewijs om te concluderen dat het type medicatie dat wordt gebruikt resulteert in statistisch significante verschillen in responstijd.

Stap 4: Rapporteer de resultaten.

Tot slot willen wij graag de testresultaten rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een Friedman-test uitgevoerd bij 10 patiënten om het effect van drie verschillende medicijnen op de responstijd te onderzoeken. Elke patiënt gebruikte elk medicijn één keer.

Uit de resultaten bleek dat het gebruikte type medicatie resulteerde in statistisch significante verschillen in responstijd (Q = 12,35, p = 0,00208).

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u de Friedman-test uitvoert met behulp van verschillende statistische software:

Hoe de Friedman-test in Excel uit te voeren
Hoe de Friedman-test uit te voeren in R
Hoe de Friedman-test in Python uit te voeren
Hoe de Friedman-test in Stata uit te voeren
Online Friedman-testcalculator