Hoe een gebogen restplot te interpreteren (met voorbeeld)

Residuele plots worden gebruikt om te beoordelen of de residuen van een regressiemodel normaal verdeeld zijn en of ze al dan niet heteroscedasticiteit vertonen.

Idealiter zou u willen dat de punten in een restdiagram willekeurig verspreid zijn rond een waarde nul, zonder duidelijk patroon.

Als u een restgrafiek tegenkomt waarin de grafiekpunten een gebogen patroon hebben, betekent dit waarschijnlijk dat het regressiemodel dat u voor de gegevens hebt opgegeven, niet correct is.

In de meeste gevallen betekent dit dat u hebt geprobeerd een lineair regressiemodel aan te passen aan een dataset die in plaats daarvan een kwadratische trend volgt.

Het volgende voorbeeld laat zien hoe u een gebogen restplot in de praktijk interpreteert (en corrigeert).

Voorbeeld: interpretatie van een gebogen restplot

Stel dat we de volgende gegevens verzamelen over het aantal gewerkte uren per week en het gerapporteerde geluksniveau (op een schaal van 0 tot 100) voor 11 verschillende mensen op een kantoor:

Als we een eenvoudig spreidingsdiagram van gewerkte uren versus geluksniveau zouden maken, zou het er zo uitzien:

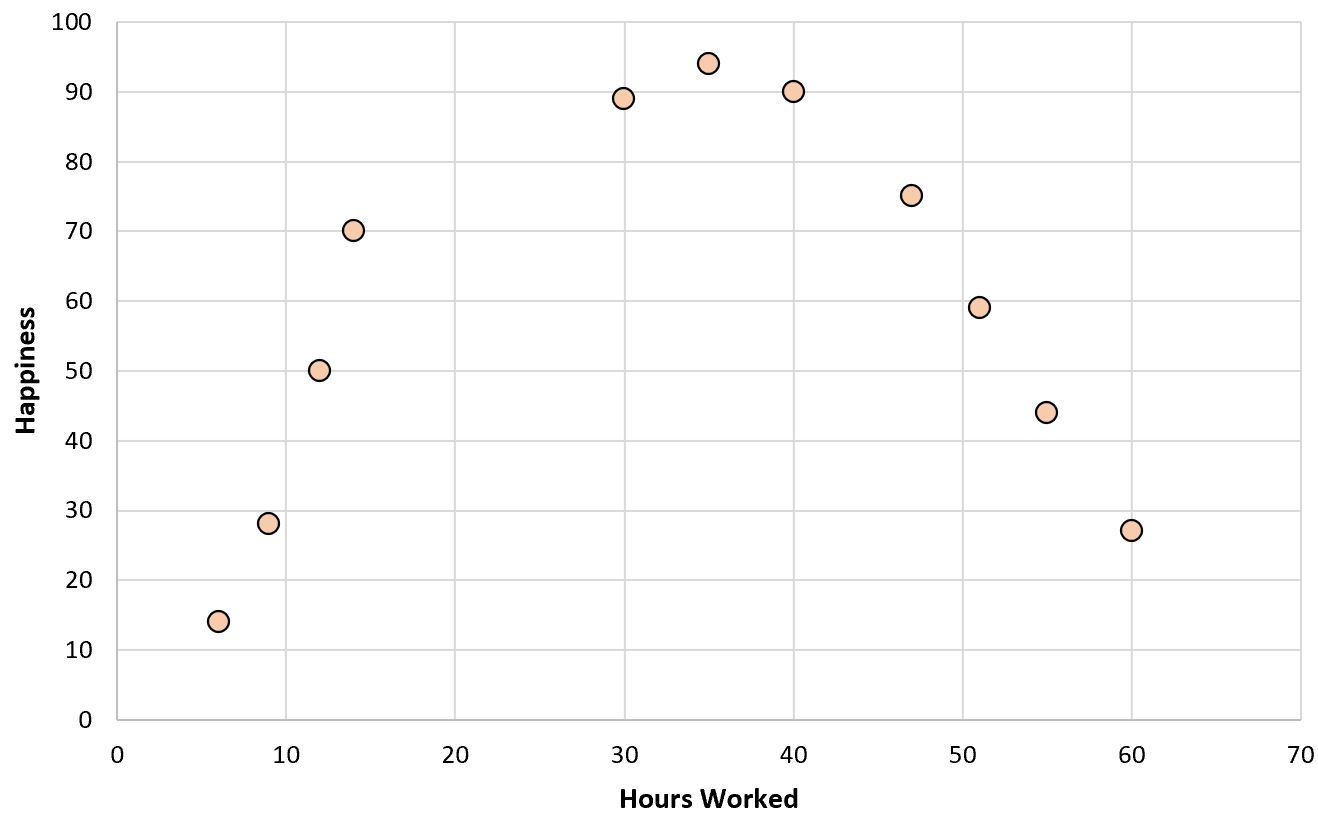
Stel nu dat we een regressiemodel willen toepassen op basis van gewerkte uren om het geluksniveau te voorspellen.

De volgende code laat zien hoe u een eenvoudig lineair regressiemodel aan deze gegevensset kunt aanpassen en een restplot in R kunt maken:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

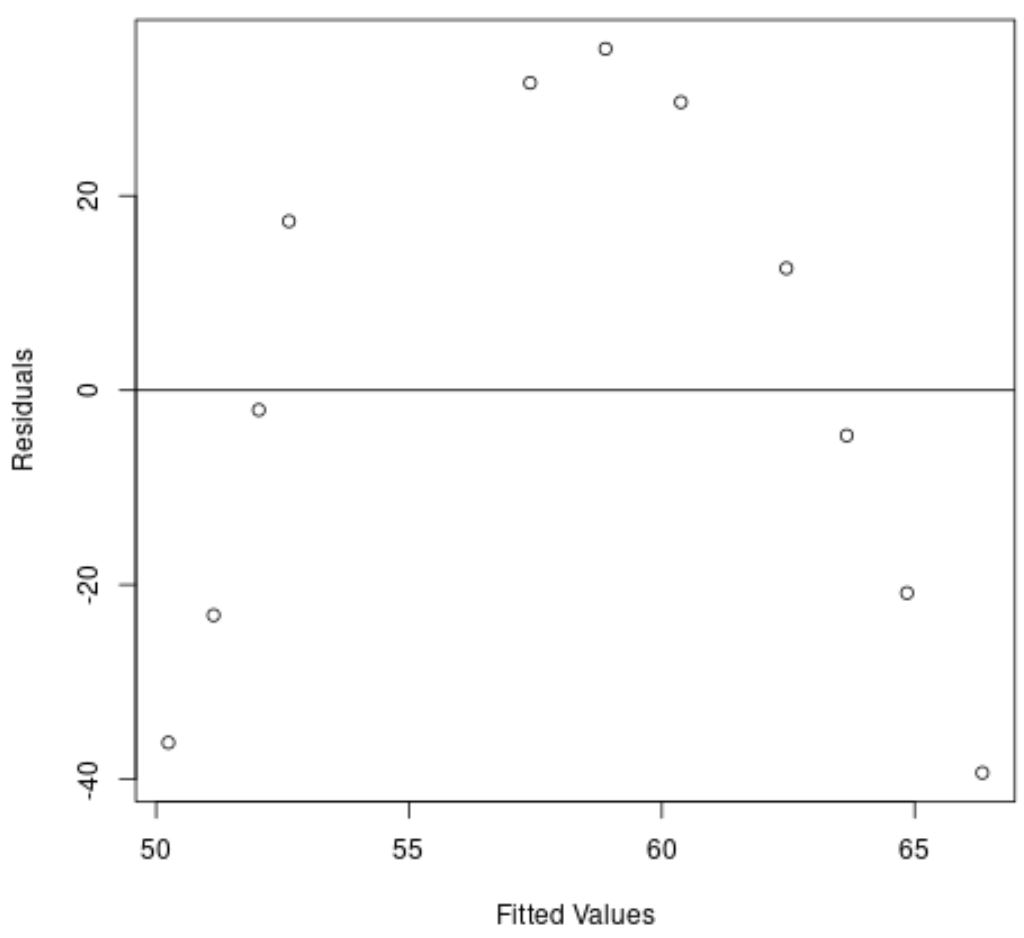
Op de x-as worden de gefitte waarden weergegeven en op de y-as de residuen.

Uit de grafiek kunnen we zien dat er een gebogen patroon in de residuen zit, wat aangeeft dat een lineair regressiemodel geen geschikte pasvorm voor deze dataset biedt.

De volgende code laat zien hoe u een kwadratisch regressiemodel aan deze gegevensset kunt aanpassen en een restgrafiek in R kunt maken:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

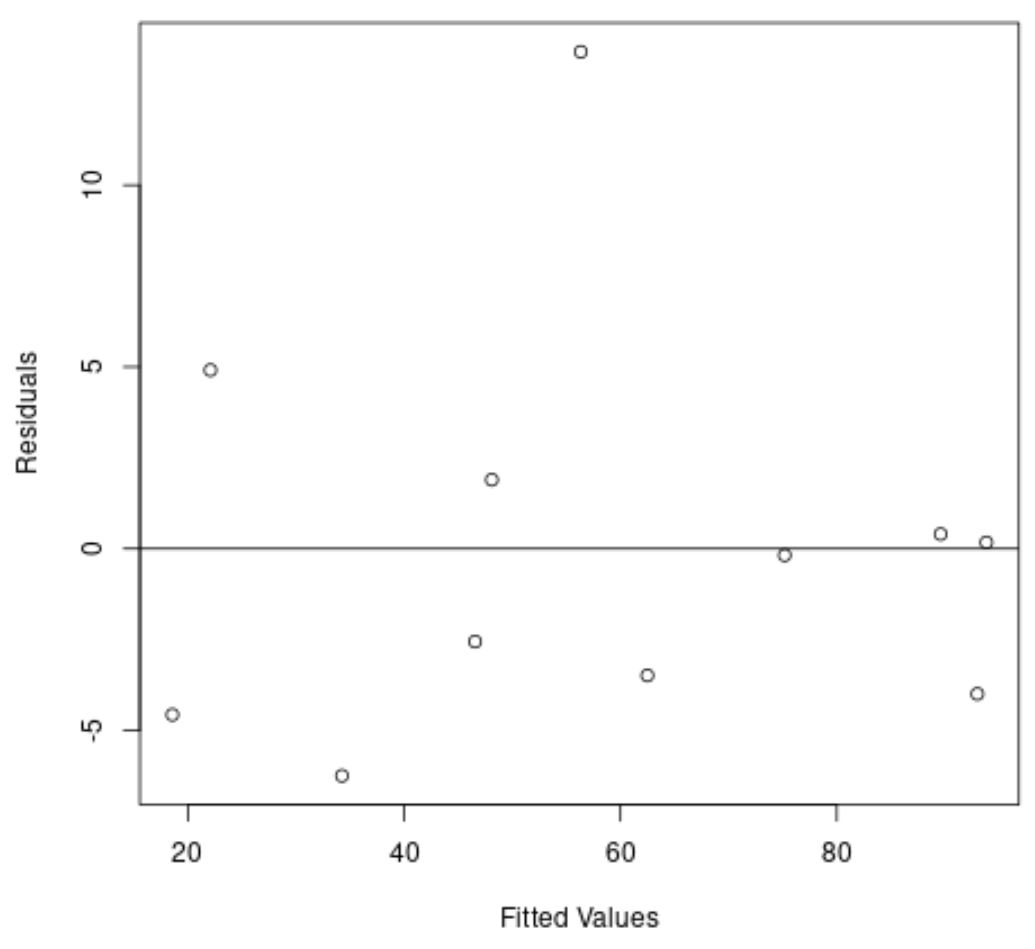
Opnieuw toont de x-as de gefitte waarden en de y-as de residuen.

Uit de grafiek kunnen we zien dat de residuen willekeurig rond nul verspreid zijn en dat er geen duidelijke trend in de residuen zit.

Dit vertelt ons dat een kwadratisch regressiemodel deze dataset veel beter past dan een lineair regressiemodel.

Dit zou logisch moeten zijn, aangezien we zagen dat de werkelijke relatie tussen gewerkte uren en geluksniveaus eerder kwadratisch dan lineair leek te zijn.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u restplots kunt maken met behulp van verschillende statistische software:

Hoe u met de hand een restpad kunt maken
Hoe maak je een restplot in R
Hoe u een restplot in Excel maakt
Hoe u een restplot maakt in Python