Hoe u een roc-curve in sas maakt

Logistische regressie is een methode die we kunnen gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is.

Om te evalueren hoe goed een logistisch regressiemodel bij een dataset past, kunnen we naar de volgende twee statistieken kijken:

• Gevoeligheid: waarschijnlijkheid dat het model een positief resultaat voorspelt voor een waarneming terwijl het resultaat daadwerkelijk positief is. Dit wordt ook wel het “echte positieve percentage” genoemd.
• Specificiteit: de kans dat het model een negatief resultaat voorspelt voor een waarneming terwijl het resultaat feitelijk negatief is. Dit wordt ook wel het ‘echte negatieve tarief’ genoemd.

Eén manier om deze twee metingen te visualiseren is door een ROC-curve te maken, wat staat voor ‘receiver operating karakteristieke’-curve. Dit is een grafiek die de gevoeligheid en specificiteit van een logistisch regressiemodel weergeeft.

In het volgende stapsgewijze voorbeeld ziet u hoe u een ROC-curve in SAS maakt en interpreteert.

Stap 1: Maak de gegevensset

Eerst zullen we voor 18 studenten een dataset maken met informatie over de volgende variabelen:

• Toelating tot een bepaalde universiteit (1 = ja, 0 = nee)
• GPA (schaal van 1 tot 4)
• ACT-score (schaal van 1 tot 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

Stap 2: Pas het logistische regressiemodel aan en creëer een ROC-curve

Vervolgens zullen we proc-logistiek gebruiken om in het logistische regressiemodel te passen, waarbij we „acceptatie“ gebruiken als de responsvariabele en „gpa“ en „act“ als de voorspellende variabelen.

We zullen afnemend specificeren, zodat SAS weet hoe de waarschijnlijkheid moet worden voorspeld dat de responsvariabele de waarde 1 aanneemt.

We zullen ook plots(only)=roc gebruiken om de ROC-curve voor het model te maken:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

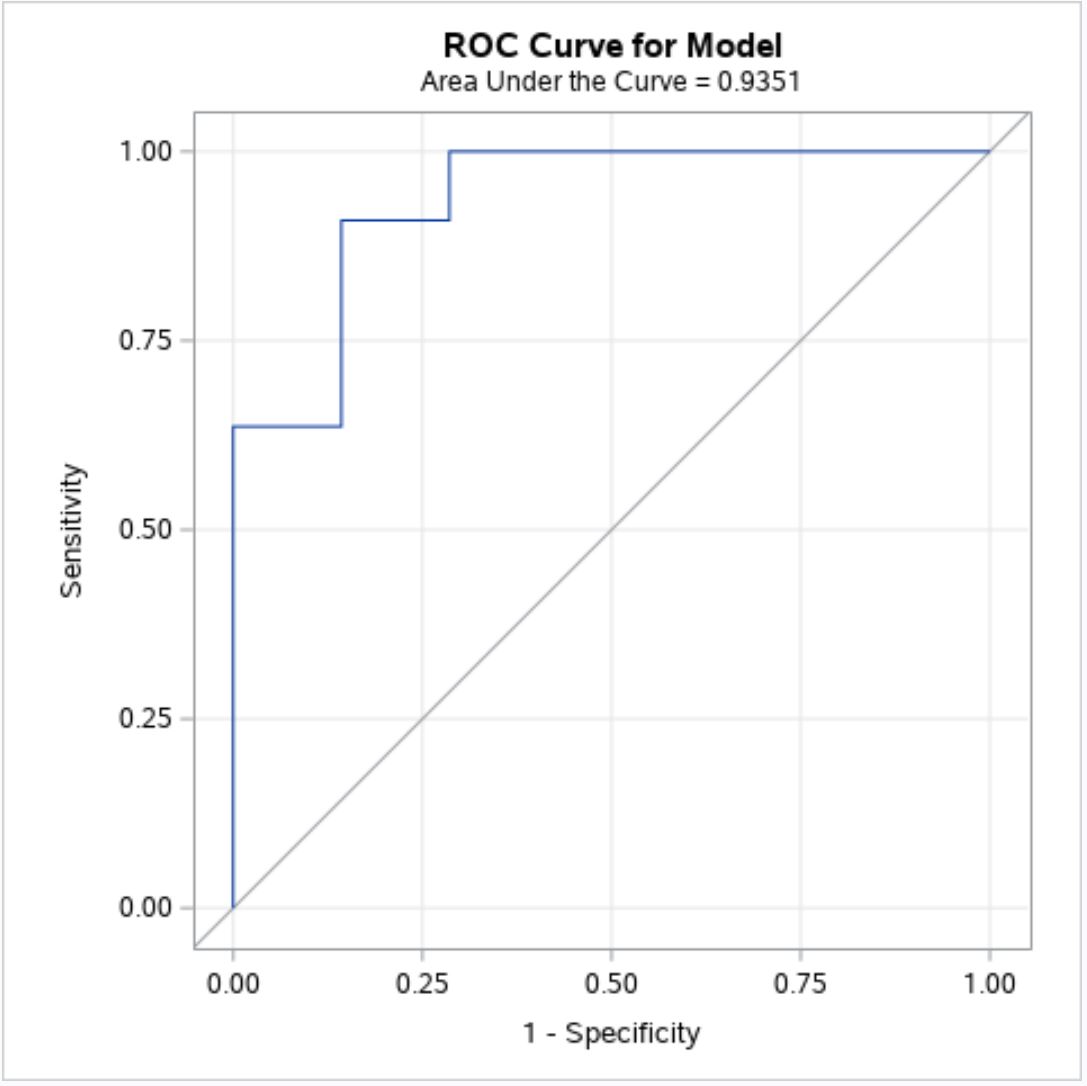
Stap 3: Interpreteer de ROC-curve

Hoe dichter de ROC-curve bij de linkerbovenhoek van de grafiek past, hoe beter het model de waarde van de responswaarden in de dataset voorspelt.

Uit de bovenstaande grafiek kunnen we zien dat de blauwe ROC-curve de neiging heeft om de linkerbovenhoek te omhelzen, wat aangeeft dat het logistische regressiemodel de waarde van de responswaarden goed kan voorspellen.

Om te kwantificeren hoe goed het logistische regressiemodel bij de gegevens past, kunnen we de AUC (gebied onder de curve) berekenen, die ons vertelt hoeveel van de grafiek zich onder de curve bevindt.

Hoe dichter de AUC bij 1 ligt, hoe beter het model. Een model met een AUC gelijk aan 0,5 is niet beter dan een model dat willekeurige classificaties uitvoert.

Onder de grafiektitel hierboven kunnen we zien dat de AUC van dit model 0,9351 is.

Omdat deze waarde dicht bij één ligt, bevestigt dit dat het model de waarde van de responswaarden goed voorspelt.

We kunnen de AUC-waarde ook gebruiken om de fit van verschillende logistische regressiemodellen te vergelijken.

Stel dat we twee verschillende logistieke regressiemodellen passen en voor elk de AUC-waarden berekenen:

• AUC van model 1: 0,9351
• AUC van model 2: 0,8140

Omdat de AUC van Model 1 groter is, vertelt dit ons dat Model 1 de gegevens beter kan aanpassen dan Model 2.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende bewerkingen in SAS uitvoert:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe logistische regressie uit te voeren in SAS