Een gebrek aan fit-test uitvoeren in r (stap voor stap)

Een gebrek aan fit-test wordt gebruikt om te bepalen of een volledig regressiemodel al dan niet een significant betere aanpassing aan een dataset biedt dan een gereduceerde versie van het model.

Laten we bijvoorbeeld zeggen dat we het aantal gestudeerde uren willen gebruiken om examenscores voor studenten aan een bepaalde hogeschool te voorspellen. We kunnen besluiten de volgende twee regressiemodellen aan te passen:

Volledig model: score = β ₀ + B ₁ (uren) + B ₂ (uren) ²

Verlaagd model: score = β ₀ + B ₁ (uren)

Het volgende stapsgewijze voorbeeld laat zien hoe u een gebrek aan fit-test in R kunt uitvoeren om te bepalen of het volledige model een significant betere fit biedt dan het gereduceerde model.

Stap 1: Creëer en visualiseer een dataset

Eerst gebruiken we de volgende code om een dataset te maken met daarin het aantal gestudeerde uren en behaalde examenscores voor 50 studenten:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Vervolgens maken we een spreidingsdiagram om de relatie tussen uren en score te visualiseren:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

Stap 2: Pas twee verschillende modellen aan de dataset toe

Vervolgens passen we twee verschillende regressiemodellen in de dataset:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

Stap 3: Voer een gebrek aan fit-test uit

Vervolgens zullen we de opdracht anova() gebruiken om een gebrek aan fit-test uit te voeren tussen de twee modellen:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De F-teststatistiek blijkt 10,554 te zijn en de overeenkomstige p-waarde is 0,002144 . Omdat deze p-waarde kleiner is dan 0,05, kunnen we de nulhypothese van de test verwerpen en concluderen dat het volledige model een statistisch significant betere fit biedt dan het gereduceerde model.

Stap 4: Visualiseer het definitieve model

Ten slotte kunnen we het uiteindelijke model (het volledige model) visualiseren aan de hand van de originele dataset:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

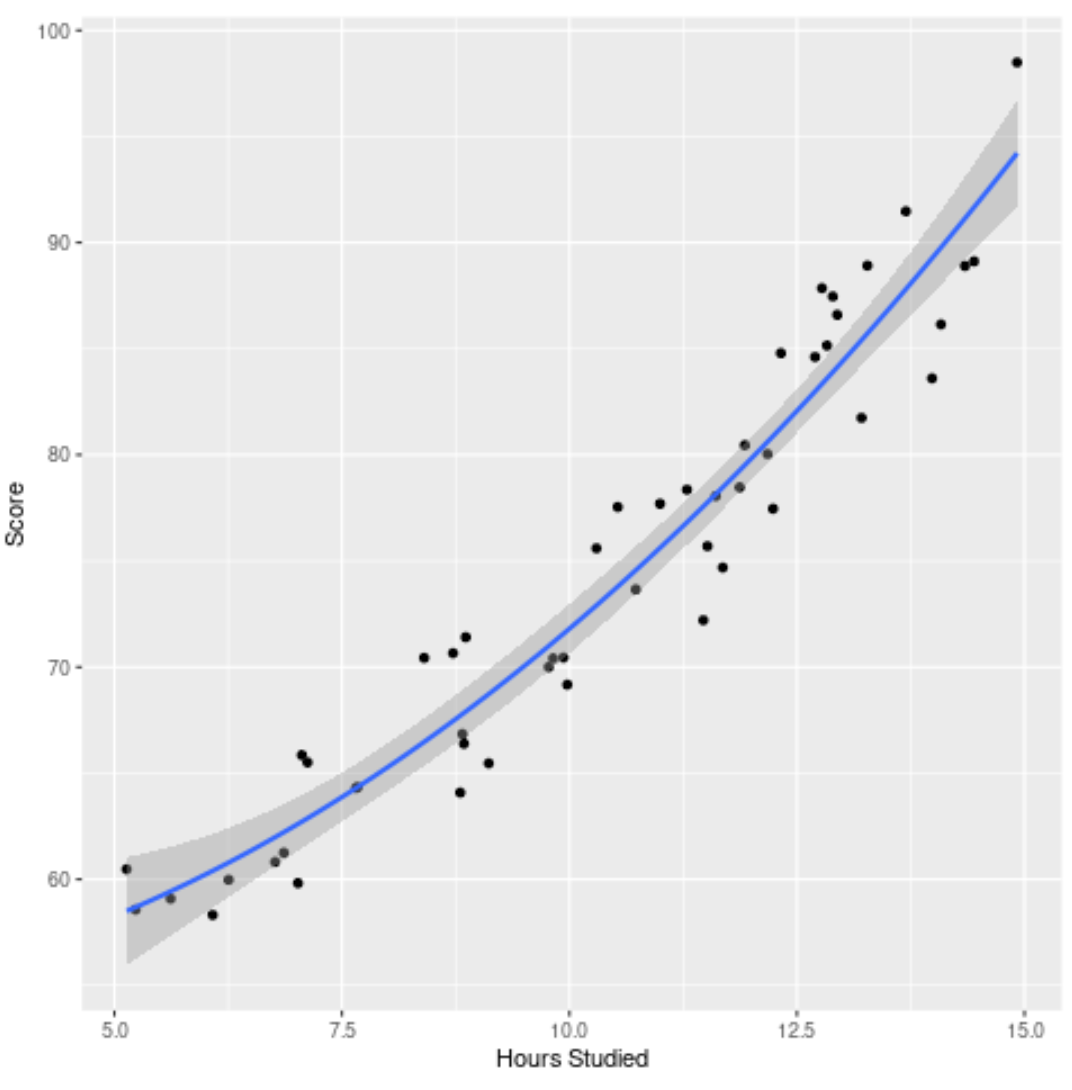
We kunnen zien dat de modelcurve vrij goed bij de gegevens past.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe polynomiale regressie uit te voeren in R