Hoe gedeeltelijke correlatie in excel te berekenen

In de statistiek gebruiken we vaak dePearson-correlatiecoëfficiënt om de lineaire relatie tussen twee variabelen te meten. Soms willen we echter de relatie tussen twee variabelen begrijpen terwijl we een derde variabele controleren .

Stel dat we bijvoorbeeld het verband willen meten tussen het aantal studie-uren van een leerling en het eindexamencijfer, terwijl we controleren voor het huidige cijfer van de leerling in de klas. In dit geval kunnen we partiële correlatie gebruiken om de relatie tussen het aantal gestudeerde uren en het eindexamencijfer te meten.

In deze tutorial wordt uitgelegd hoe u een gedeeltelijke correlatie in Excel berekent.

Voorbeeld: gedeeltelijke correlatie in Excel

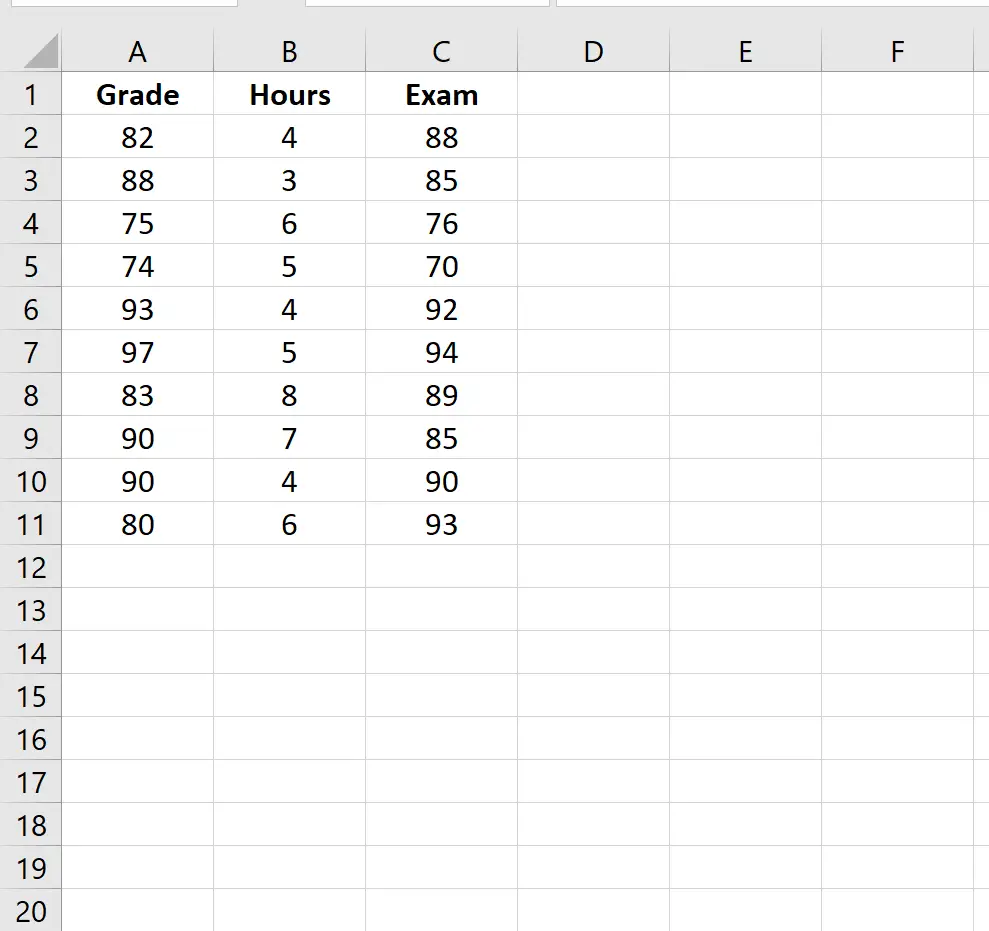
Laten we zeggen dat we een dataset hebben die de volgende informatie weergeeft voor 10 studenten:

• Huidig cijfer in een klas
• Uren besteed aan studeren voor het eindexamen
• Eindexamenscore

Gebruik de volgende stappen om de gedeeltelijke correlatie tussen het aantal gestudeerde uren en het examencijfer te vinden, terwijl u controleert voor het huidige cijfer.

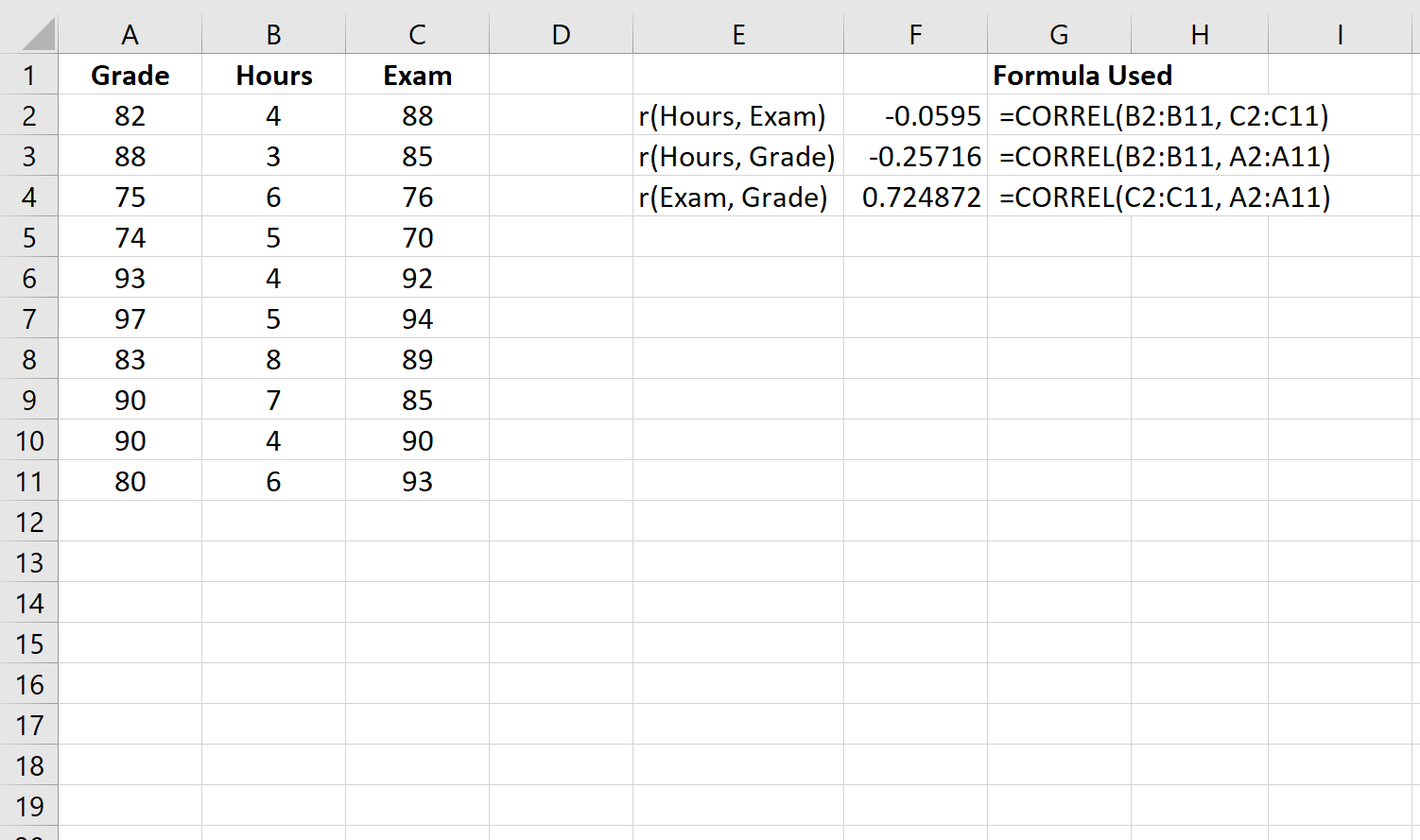
Stap 1: Bereken elke paarsgewijze correlatie.

Eerst berekenen we de correlatie tussen elke paarsgewijze combinatie van variabelen:

Stap 2: Bereken de gedeeltelijke correlatie tussen uren en examenscore.

De formule om de gedeeltelijke correlatie tussen variabele A en variabele B te berekenen terwijl voor variabele C wordt gecontroleerd, is als volgt:

Gedeeltelijke correlatie = (r _A,B – r _A,C *r _B,C ) / √((1-r ² _A,B )(1-r ² _B,C ))

De volgende schermafbeelding laat zien hoe je deze formule kunt gebruiken om de gedeeltelijke correlatie tussen uren en examencijfer te berekenen, waarbij wordt gecontroleerd voor het huidige cijfer:

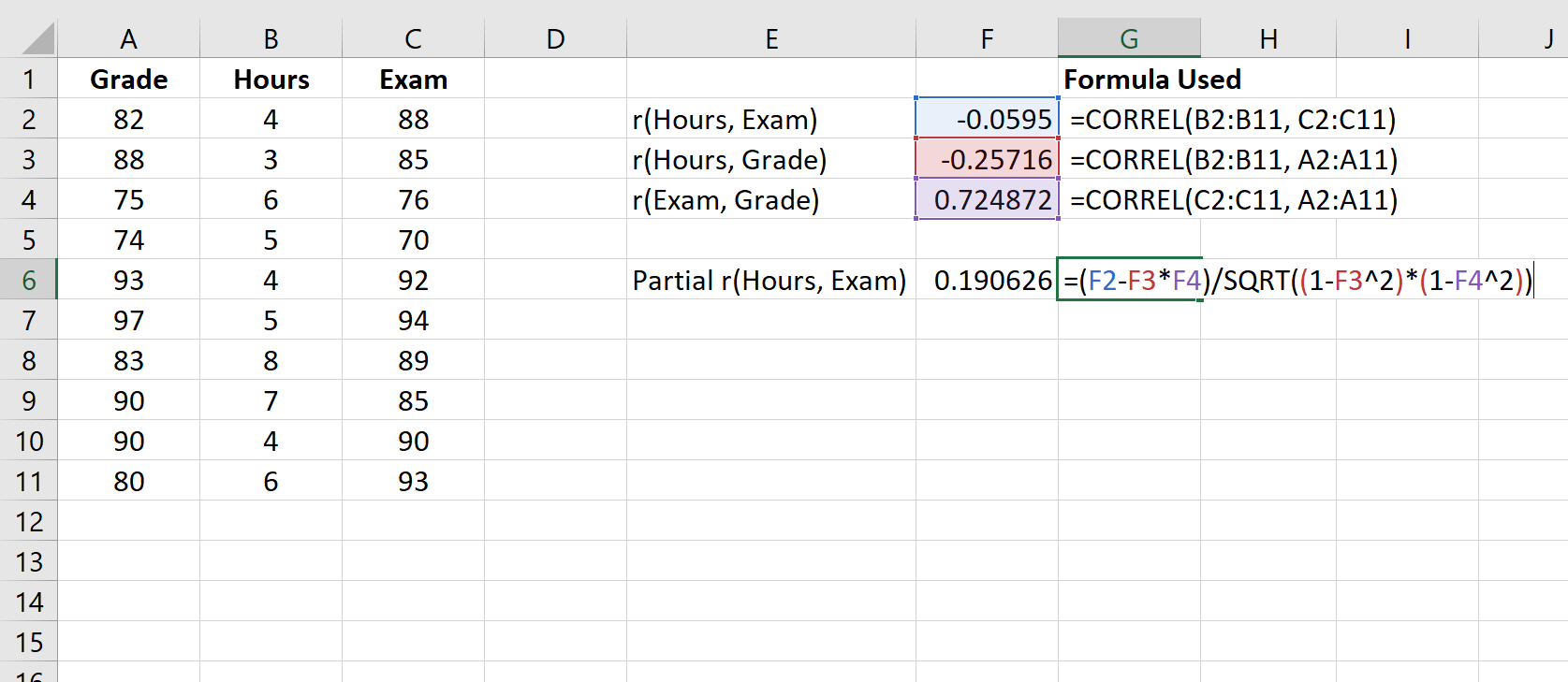
De gedeeltelijke correlatie is 0,190626 . Om te bepalen of deze correlatie statistisch significant is, kunnen we de overeenkomstige p-waarde vinden.

Stap 3: Bereken de p-waarde van de gedeeltelijke correlatie.

De t- teststatistiek kan als volgt worden berekend:

t = r√(n-3) / √(1-r ² )

De volgende schermafbeelding laat zien hoe u deze formule kunt gebruiken om de teststatistiek en de bijbehorende p-waarde te berekenen:

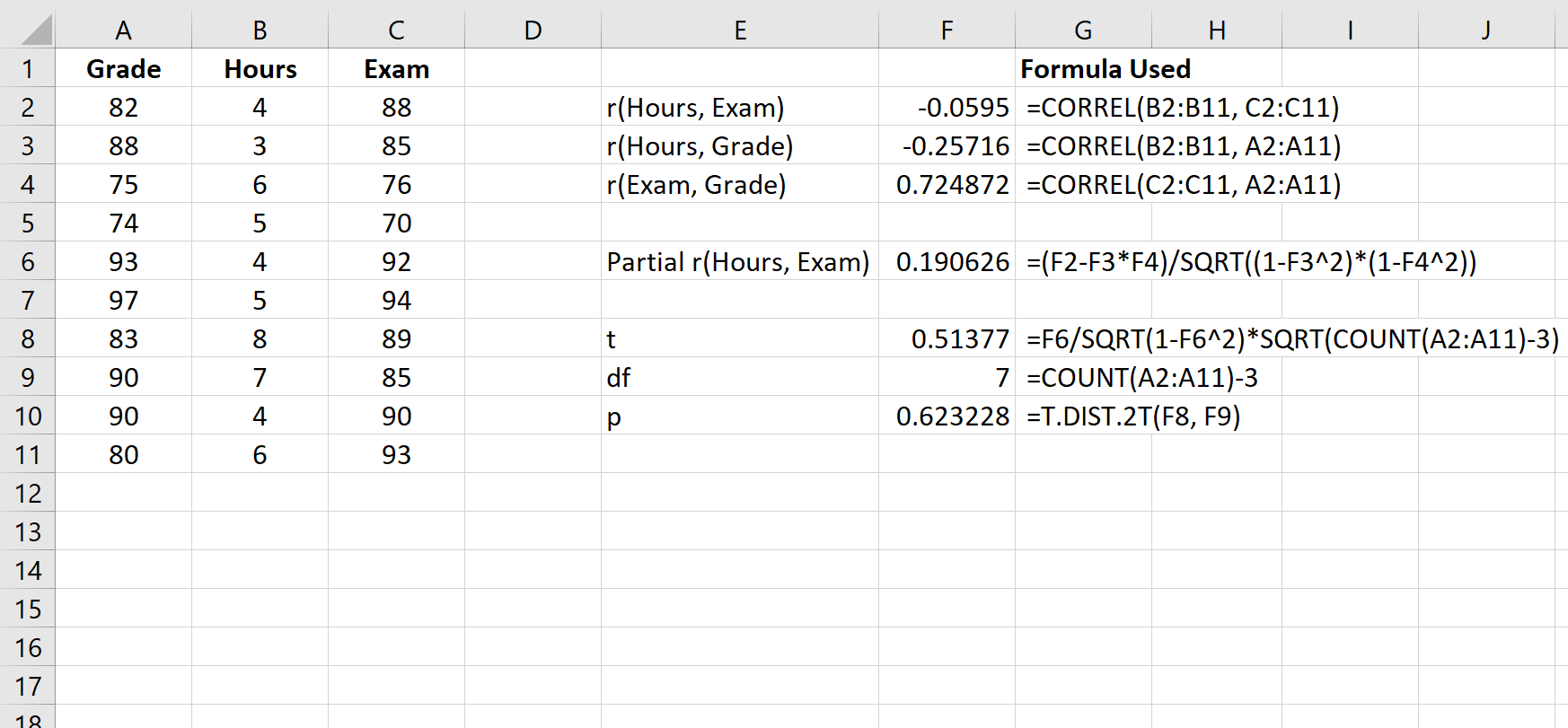
De t- teststatistiek is 0,51377 . Het totale aantal vrijheidsgraden is n-3 = 10-3 = 7 . De overeenkomstige p-waarde is 0,623228 . Omdat deze waarde niet kleiner is dan 0,05 betekent dit dat de deelcorrelatie tussen uren en examenresultaten niet statistisch significant is.