Hoe u een gedeeltelijke f-test uitvoert in excel
Om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen een regressiemodel en een geneste versie van hetzelfde model, wordt een gedeeltelijke F-test gebruikt.
Een genest model is eenvoudigweg een model dat een subset van voorspellende variabelen in het algehele regressiemodel bevat.
Stel dat we bijvoorbeeld het volgende regressiemodel hebben met vier voorspellende variabelen:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
Een voorbeeld van een genest model is het volgende model met slechts twee van de oorspronkelijke voorspellende variabelen:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
Om te bepalen of deze twee modellen significant van elkaar verschillen, kunnen we een gedeeltelijke F-test uitvoeren, die de volgende F-teststatistiek berekent:
F = (( Verminderde RSS – Volledige RSS)/p) / ( Volledige RSS /nk)
Goud:
- Gereduceerde RSS : de resterende kwadratensom van het gereduceerde (dwz “geneste”) model.
- RSS full : De resterende kwadratensom van het volledige model.
- p: aantal voorspellers verwijderd uit het volledige model.
- n: het totale aantal waarnemingen in de dataset.
- k: Het aantal coëfficiënten (inclusief het snijpunt) in het volledige model.
Deze test maakt gebruik van de volgende nul- en alternatieve hypothesen :
H 0 : Alle uit het volledige model verwijderde coëfficiënten zijn nul.
H A : Ten minste één van de uit het volledige model verwijderde coëfficiënten is niet nul.
Als de p-waarde die overeenkomt met de F-toetsstatistiek onder een bepaald significantieniveau ligt (bijvoorbeeld 0,05), dan kunnen we de nulhypothese verwerpen en concluderen dat ten minste één van de uit het volledige model verwijderde coëfficiënten significant is.
In het volgende voorbeeld ziet u hoe u een gedeeltelijke F-test uitvoert in Excel.
Voorbeeld: gedeeltelijke F-test in Excel
Stel dat we de volgende gegevensset in Excel hebben:
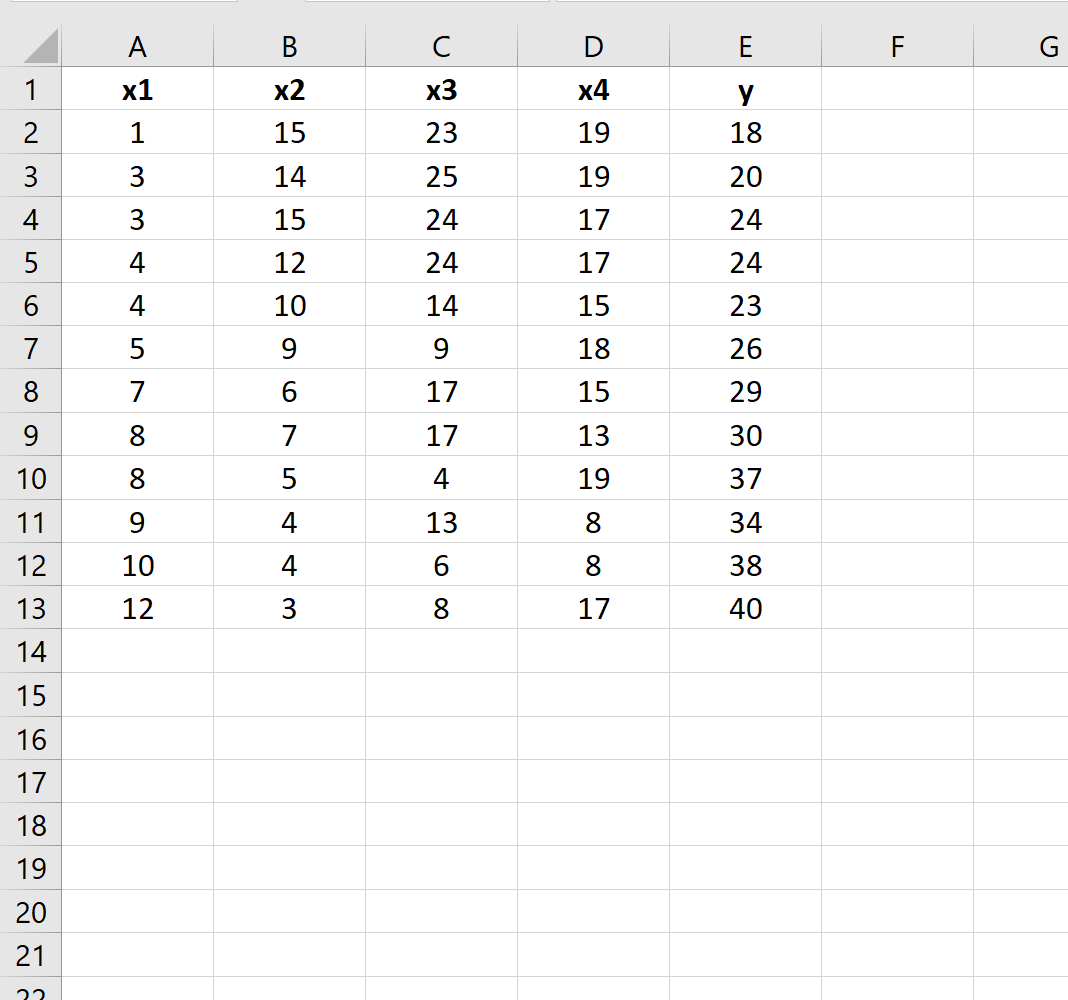
Stel dat we willen bepalen of er een verschil is tussen de volgende twee regressiemodellen:
Compleet model: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Gereduceerd model: y = β 0 + β 1 x 1 + β 2 x 2
We kunnen voor elk model een meervoudige lineaire regressie in Excel uitvoeren om het volgende resultaat te verkrijgen:
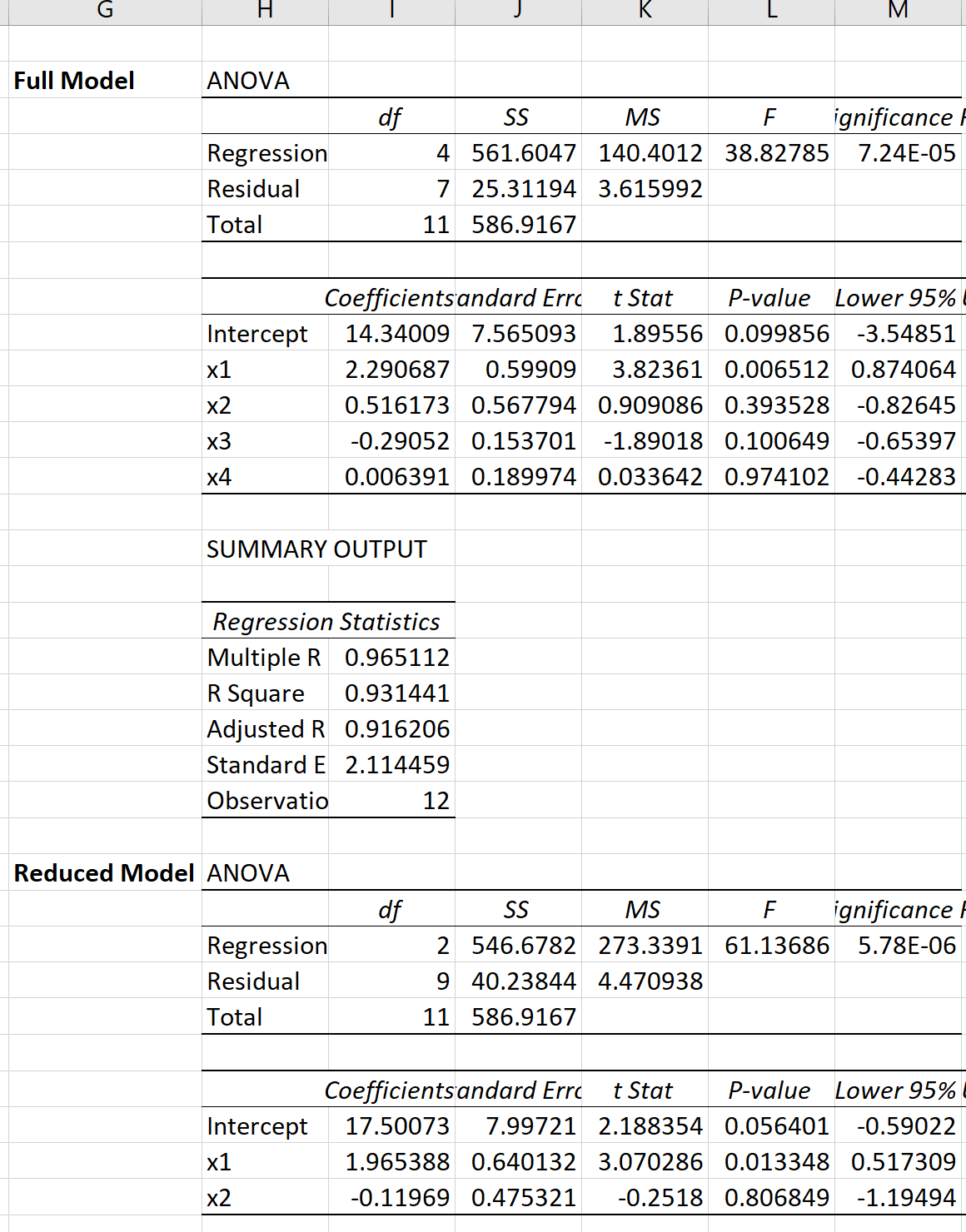
We kunnen dan de volgende formule gebruiken om de F-teststatistiek voor de gedeeltelijke F-test te berekenen:
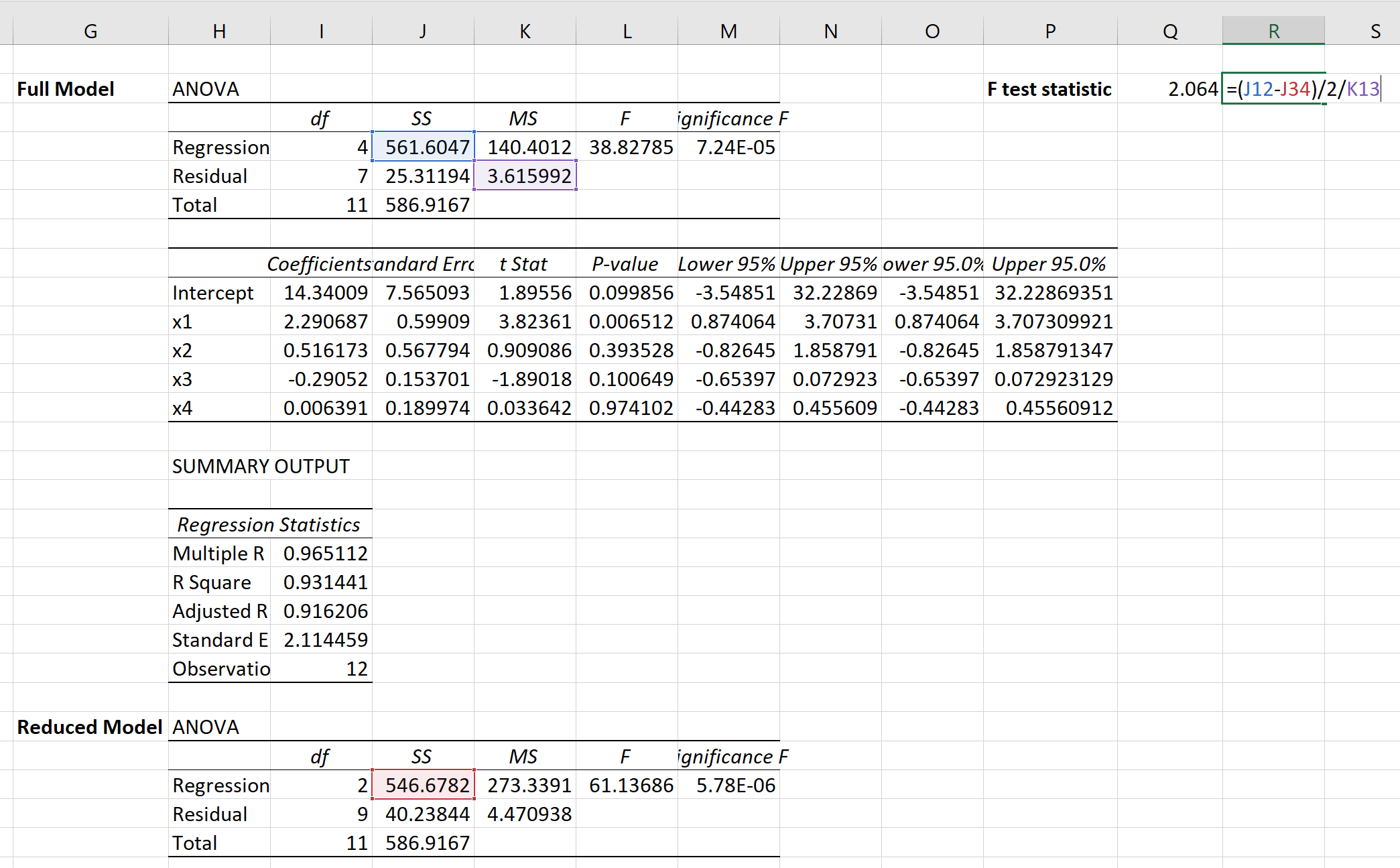
De teststatistiek blijkt 2,064 te zijn.
We kunnen dan de volgende formule gebruiken om de overeenkomstige p-waarde te berekenen:
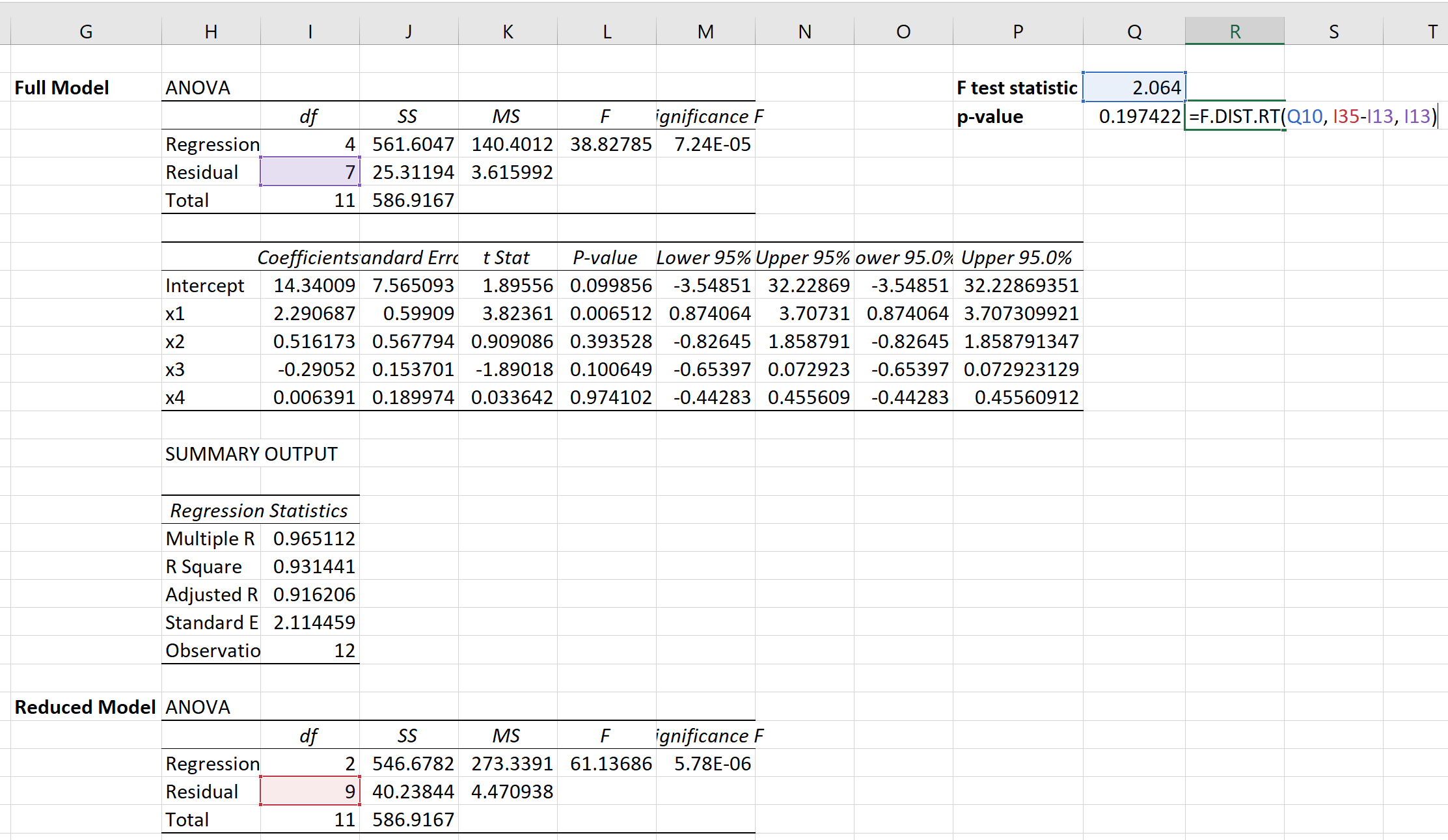
De p-waarde blijkt 0,1974 te zijn.
Omdat deze p-waarde niet kleiner is dan 0,05, zullen we er niet in slagen de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat een van de x3 of x4 voorspellende variabelen statistisch significant is.
Met andere woorden: het toevoegen van x3 en x4 aan het regressiemodel verbetert de modelfit niet significant.
Aanvullende bronnen
Hoe u eenvoudige lineaire regressie uitvoert in Excel
Hoe u meerdere lineaire regressies uitvoert in Excel
Hoe de standaardfout van regressie in Excel te berekenen
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder