Hoe u gedeeltelijke restplots kunt maken in r

Meervoudige lineaire regressie is een statistische methode die we kunnen gebruiken om de relatie tussen meerdere voorspellende variabelen en eenresponsvariabele te begrijpen.

Een van de belangrijkste aannames van meervoudige lineaire regressie is echter dat er een lineair verband bestaat tussen elke voorspellende variabele en de responsvariabele.

Als niet aan deze veronderstelling wordt voldaan, zijn de resultaten van het regressiemodel mogelijk niet betrouwbaar.

Eén manier om deze aanname te testen is door een partiële residuenplot te maken, waarin de residuen van een voorspellende variabele worden weergegeven ten opzichte van de responsvariabele.

In het volgende voorbeeld ziet u hoe u gedeeltelijke residuele plots maakt voor een regressiemodel in R.

Voorbeeld: Hoe u gedeeltelijke restplots kunt maken in R

Stel dat we een regressiemodel passen met drie voorspellende variabelen in R:

 #make this example reproducible
set. seeds (0)

#define response variable
y <- c(1:1000)

#define three predictor variables
x1 <- c(1:1000)*runif(n=1000)
x2 <- (c(1:1000)*rnorm(n=1000))^2
x3 <- (c(1:1000)*rnorm(n=1000))^3

#fit multiple linear regression model
model <- lm(y~x1+x2+x3))

We kunnen de functie crPlots() uit het car- pakket in R gebruiken om gedeeltelijke residuele plots te maken voor elke voorspellende variabele in het model:

 library (car)

#create partial residual plots
crPlots(model)

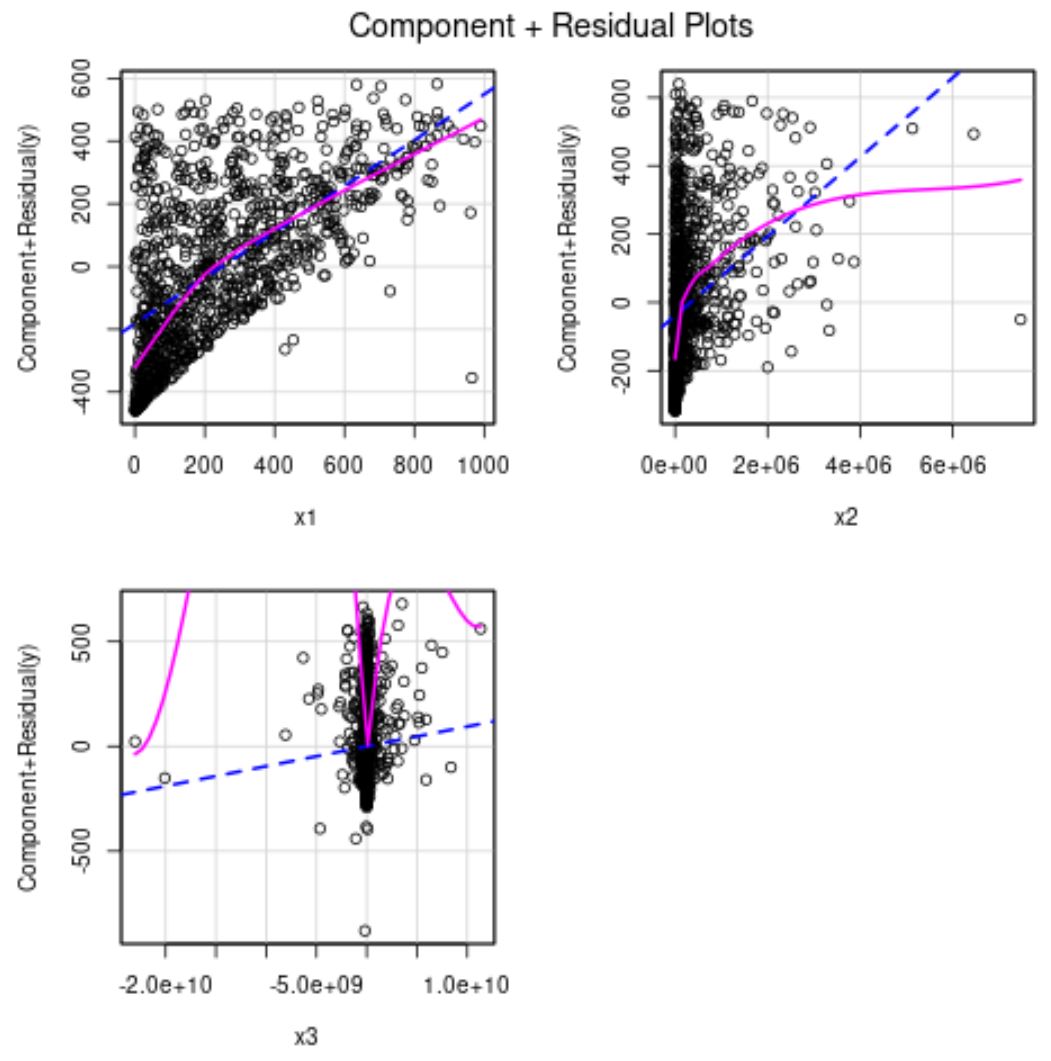
De blauwe lijn toont de verwachte residuen als de relatie tussen de voorspeller en de responsvariabele lineair was. De roze lijn geeft de daadwerkelijke residuen weer.

Als de twee lijnen significant verschillen, duidt dit op een niet-lineair verband.

Uit de bovenstaande grafieken kunnen we zien dat de residuen voor x2 en x3 niet-lineair lijken.

Dit is in strijd met de lineariteitsaanname van meervoudige lineaire regressie. Eén manier om dit probleem op te lossen is door een vierkantswortel- of kubieke worteltransformatie te gebruiken voor de voorspellende variabelen:

 library (car)

#fit new model with transformed predictor variables
model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3)))

#create partial residual plots for new model
crPlots(model_transformed)

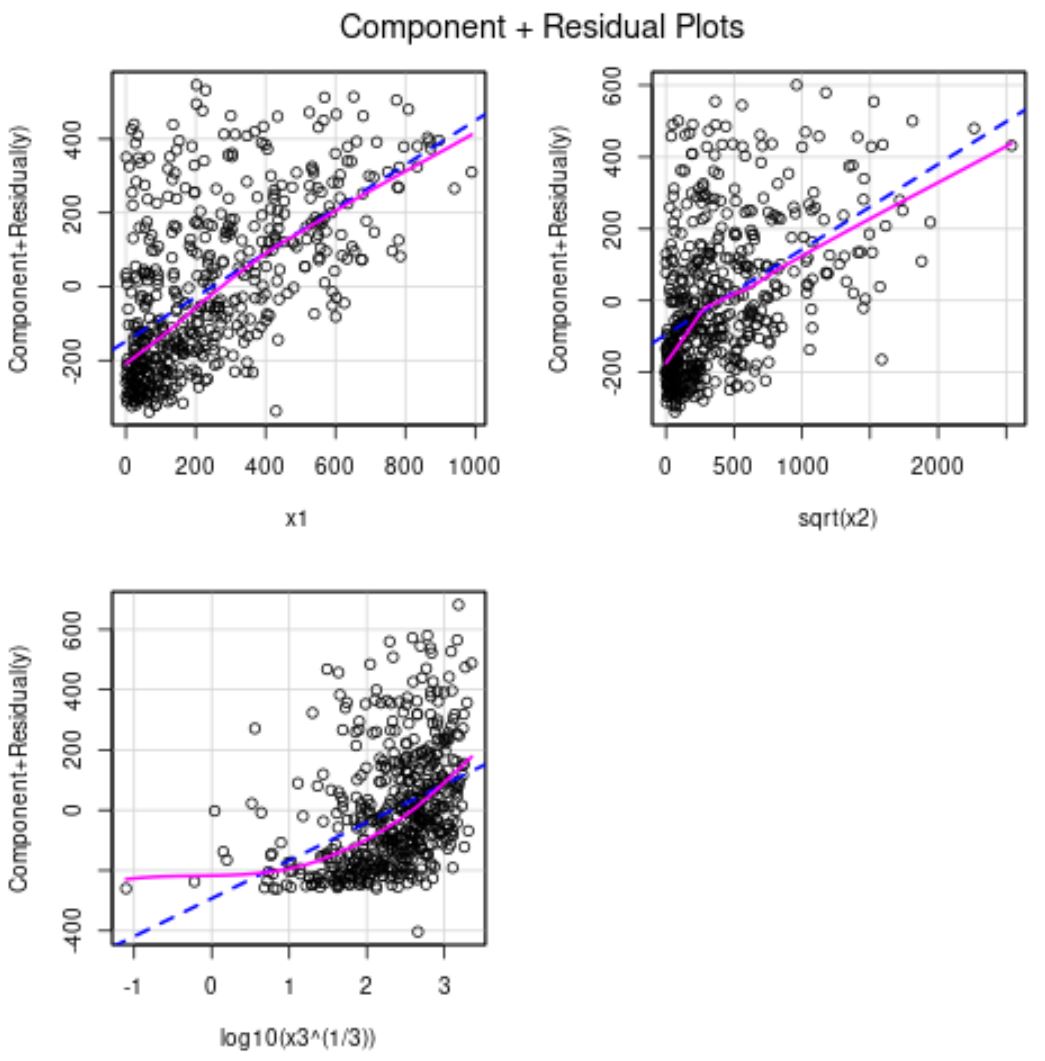
Uit de gedeeltelijke residuele grafieken kunnen we zien dat x2 nu een meer lineaire relatie heeft met de responsvariabele.

De x3-voorspellingsvariabele is nog steeds enigszins niet-lineair, dus we kunnen besluiten een andere transformatie uit te proberen of de variabele mogelijk helemaal uit het model te verwijderen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende plots in R kunt maken:

Hoe diagnostische plots te maken in R
Hoe u een schaal- en locatieplot maakt in R
Hoe maak je een restplot in R