Gegevens transformeren in python (logboek, vierkantswortel, kubuswortel)

Veel statistische tests gaan ervan uit dat datasets normaal verdeeld zijn. In de praktijk is dit echter vaak niet het geval.

Eén manier om dit probleem op te lossen is door de verdeling van waarden in een dataset te transformeren met behulp van een van de volgende drie transformaties:

1. Logtransformatie: transformeer de responsvariabele van y naar log(y) .

2. Vierkantsworteltransformatie: Transformeer de responsvariabele van y naar √y .

3. Derdemachtsworteltransformatie: transformeer de responsvariabele van y naar y ^1/3 .

Door deze transformaties uit te voeren, wordt de dataset doorgaans normaler verdeeld.

De volgende voorbeelden laten zien hoe u deze transformaties in Python kunt uitvoeren.

Logboektransformatie in Python

De volgende code laat zien hoe u een logaritmische transformatie op een variabele uitvoert en zij-aan-zij plots maakt om de oorspronkelijke distributie en de log-getransformeerde distributie van de gegevens weer te geven:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 4 , b= 15 , size= 300 )

#create log-transformed data
data_log = np. log (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Log-Transformed Data ')

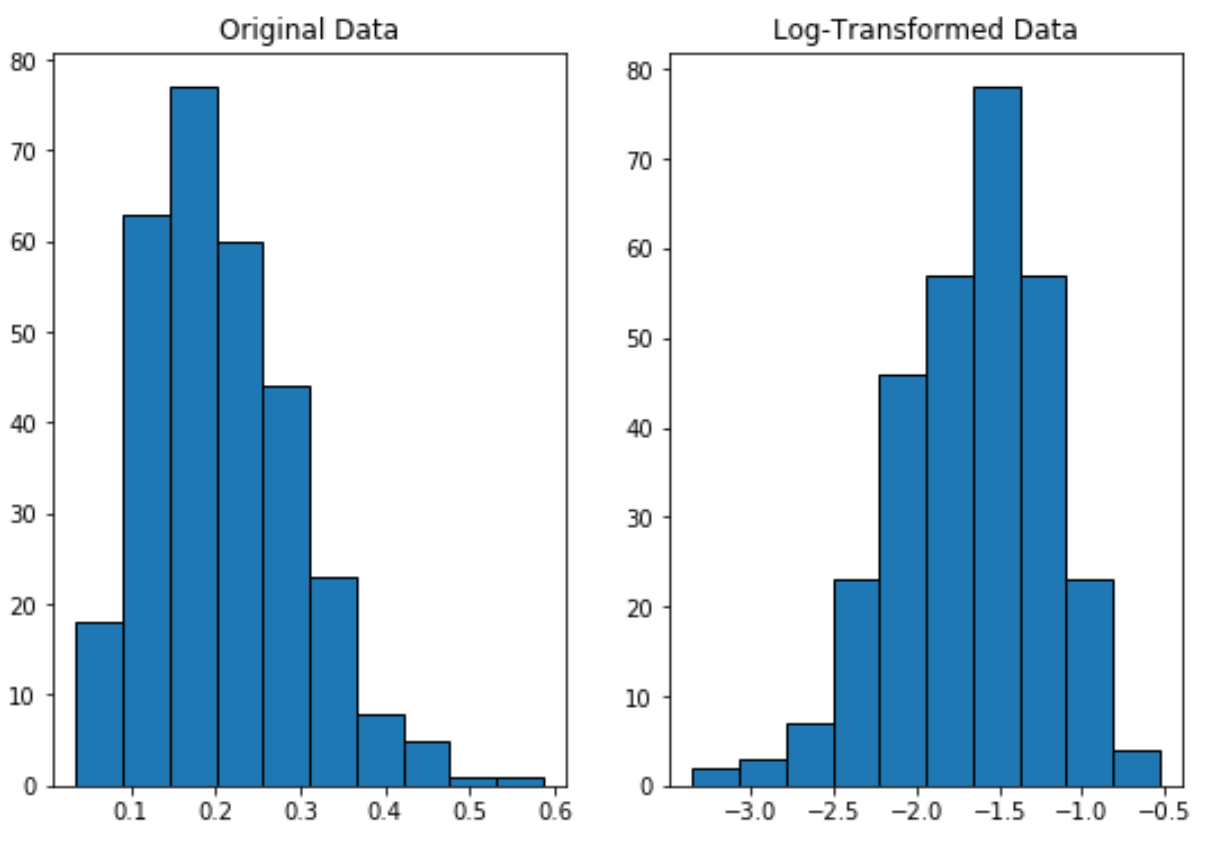
Merk op hoe de log-getransformeerde distributie normaler verdeeld is dan de oorspronkelijke distributie.

Het is nog steeds geen perfecte „klokvorm“, maar het ligt dichter bij een normale verdeling dan de oorspronkelijke verdeling.

Vierkantsworteltransformatie in Python

De volgende code laat zien hoe u een vierkantsworteltransformatie op een variabele uitvoert en zij-aan-zij plots maakt om de oorspronkelijke distributie en de getransformeerde vierkantswortelverdeling van de gegevens weer te geven:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. sqrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Square Root Transformed Data ') 

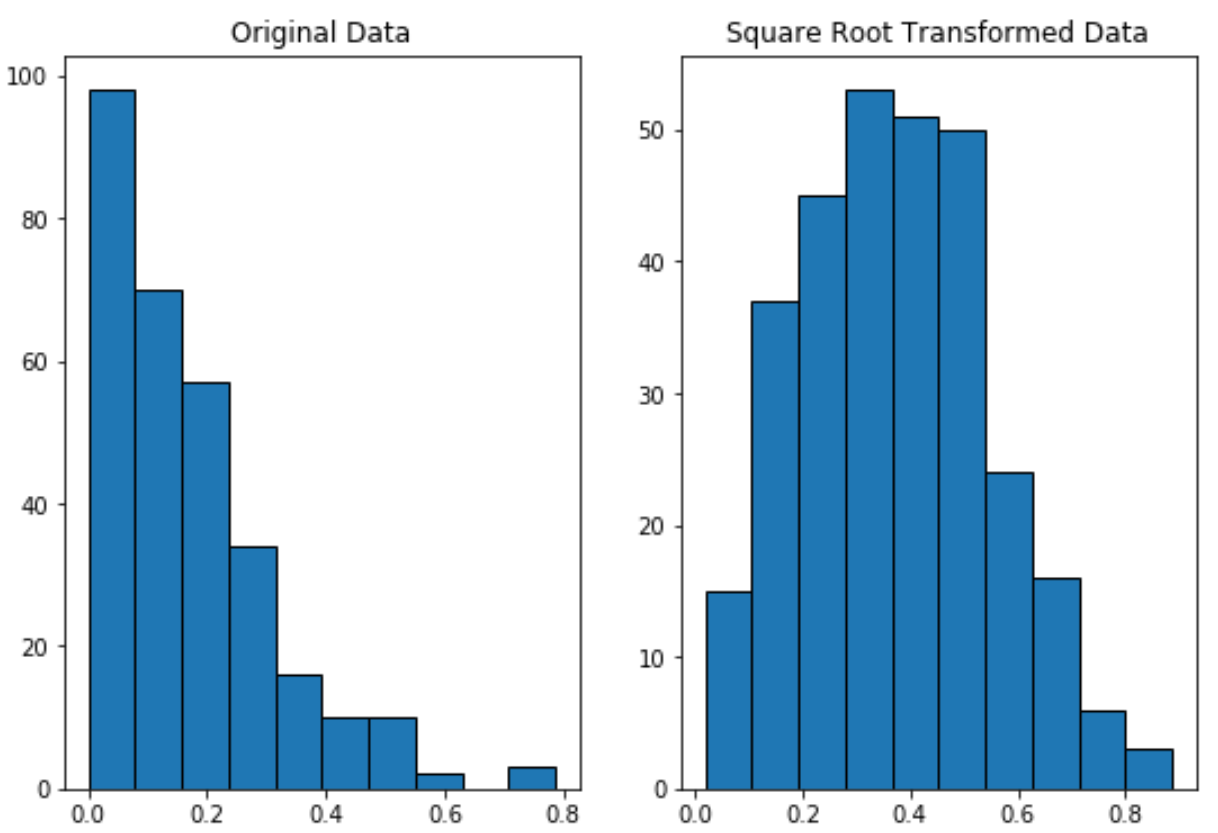
Merk op hoe de met de vierkantswortel getransformeerde gegevens veel normaler verdeeld zijn dan de oorspronkelijke gegevens.

Kubusworteltransformatie in Python

De volgende code laat zien hoe u een derdemachtsworteltransformatie op een variabele uitvoert en zij-aan-zij-plots maakt om de oorspronkelijke verdeling en de getransformeerde derdemachtswortelverdeling van de gegevens weer te geven:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. cbrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Cube Root Transformed Data ') 

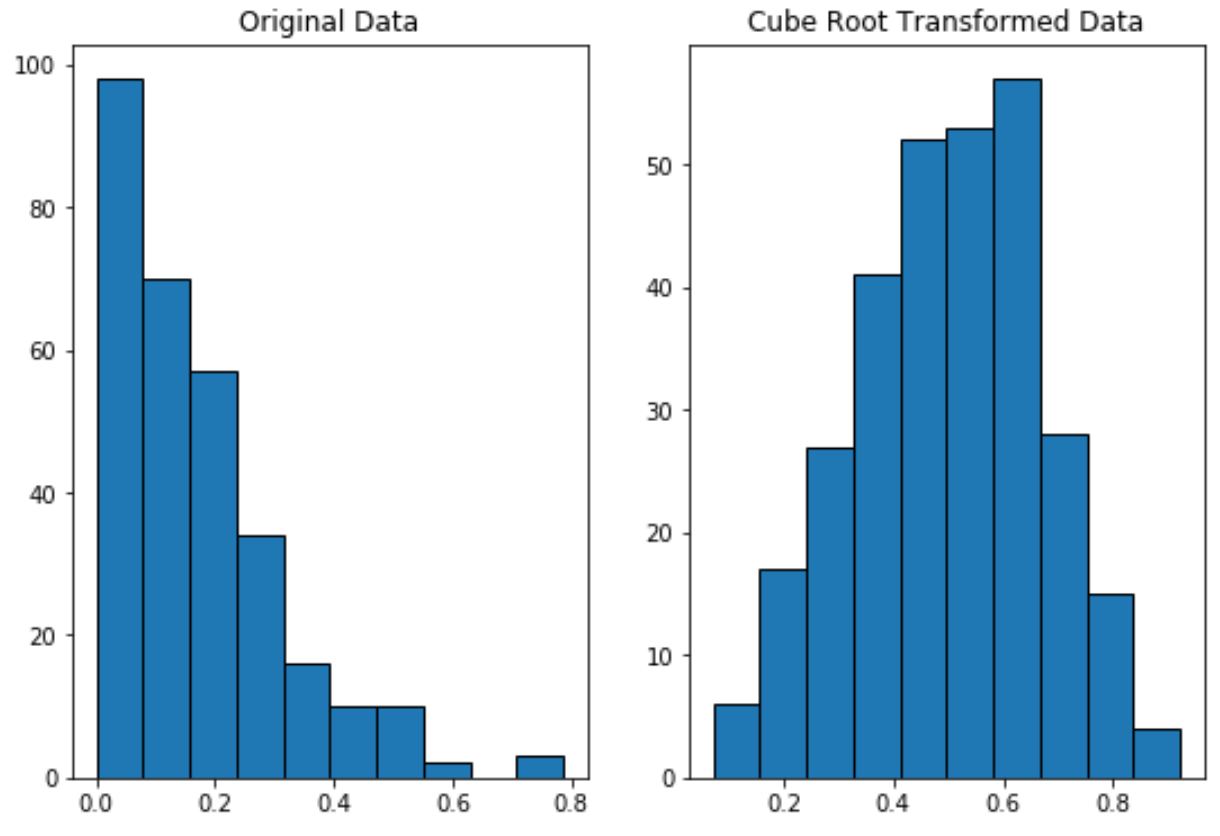
Merk op dat de getransformeerde gegevens uit de derdemachtswortel veel normaler verdeeld zijn dan de oorspronkelijke gegevens.

Aanvullende bronnen

Hoe Z-scores in Python te berekenen
Hoe gegevens in Python te normaliseren
Wat is de normaliteitsaanname in de statistiek?