Hoe u de gegroepeerde gegevensmodus kunt vinden: met voorbeelden

We willen vaak berekenen hoe gegevens op de een of andere manier worden gegroepeerd.

Houd er rekening mee dat de modus de waarde vertegenwoordigt die het vaakst voorkomt.

Stel dat we bijvoorbeeld de volgende gegroepeerde gegevens hebben:

Hoewel het niet mogelijk is om de exacte modus te berekenen, omdat we de ruwe gegevenswaarden niet kennen, is het mogelijk om de modus te schatten met behulp van de volgende formule:

Gegroepeerde gegevensmodus = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]

Goud:

• L : Ondergrens van de modale klasse
• W : Breedte van de modale klasse
• _Fm : Modale klassefrequentie
• F ₁ : Frequentie van de cursus onmiddellijk vóór de modale cursus
• F ₂ : Cursusfrequentie direct na de modale cursus

Opmerking : de modale klasse is eenvoudigweg de klasse met de hoogste frequentie. In het bovenstaande voorbeeld zou de modale klasse 21-30 zijn, omdat deze de hoogste frequentie heeft.

De volgende voorbeelden laten zien hoe u de modus van gegroepeerde gegevens in verschillende scenario’s kunt berekenen.

Voorbeeld 1: Bereken de modus van gegroepeerde gegevens

Stel dat we de volgende frequentieverdeling hebben die het examen laat zien dat door 40 studenten in een bepaalde klas is beoordeeld:

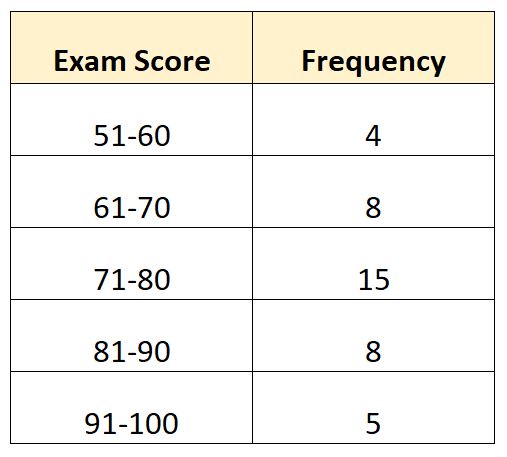
In dit voorbeeld is de modale klasse 71-80.

Als we dit weten, kunnen we de volgende waarden berekenen:

• L : Ondergrens van modale klasse: 71
• W : Breedte modale klasse: 9
• _Fm : Modale klassefrequentie: 15
• F ₁ : Frequentie van de cursus onmiddellijk vóór de modale cursus: 8
• F ₂ : Frequentie van de cursus onmiddellijk na de modale cursus: 8

We kunnen deze waarden in de formule pluggen om de distributiemodus te berekenen:

• Modus = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Modus = 71 + 9[(15-8) / ( (15-8) + (15-8) )]
• Modus = 75,5

Wij schatten de modale examenscore op 75,5 .

Voorbeeld 2: Bereken de modus van gegroepeerde gegevens

Stel dat we de volgende frequentieverdeling hebben die het aantal punten weergeeft dat per wedstrijd door 60 basketbalspelers is gescoord:

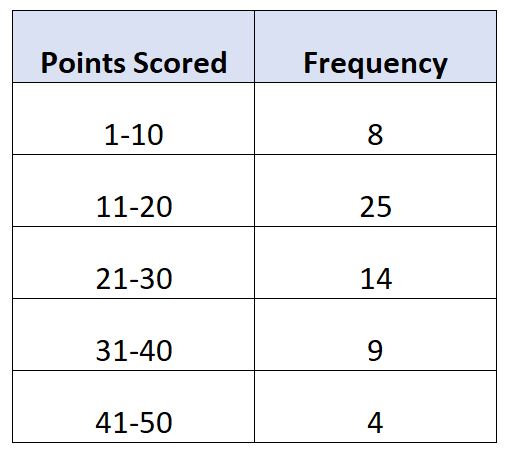
In dit voorbeeld is de modale klasse 11-20.

Als we dit weten, kunnen we de volgende waarden berekenen:

• L : Ondergrens van modale klasse: 11
• W : Breedte modale klasse: 9
• F _m : Modale klassefrequentie: 25
• F ₁ : Frequentie van de cursus onmiddellijk vóór de modale cursus: 8
• F ₂ : Cursusfrequentie direct na de modale cursus: 14

We kunnen deze waarden in de formule pluggen om de distributiemodus te berekenen:

• Modus = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Modus = 11 + 9[(25-8) / ( (25-8) + (25-14) )]
• Mode = 16.46

Wij schatten dat het aantal gescoorde modale punten 16,46 bedraagt.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende bewerkingen met gegroepeerde gegevens kunt uitvoeren:

Hoe u het gemiddelde en de standaardafwijking van gegroepeerde gegevens kunt vinden
Hoe u de mediaan van gegroepeerde gegevens kunt vinden
Hoe u de percentielrangschikking voor gegroepeerde gegevens kunt berekenen