Hoe te bepalen of een kansverdeling geldig is

Een kansverdeling vertelt ons de waarschijnlijkheid dat een willekeurige variabele bepaalde waarden aanneemt.

Om een kansverdeling geldig te laten zijn, moet deze aan twee eisen voldoen:

1. Elke waarschijnlijkheid moet tussen 0 en 1 liggen.

2. De som van de kansen moet opgeteld 1 zijn.

Als aan deze twee voorwaarden is voldaan, is de kansverdeling geldig.

De volgende voorbeelden laten zien hoe u kunt controleren of verschillende kansverdelingen geldig zijn.

Voorbeeld 1: Doelpunten gescoord in een voetbalwedstrijd

De volgende kansverdeling geeft de kans weer dat een bepaald voetbalteam een bepaald aantal doelpunten scoort in een wedstrijd:

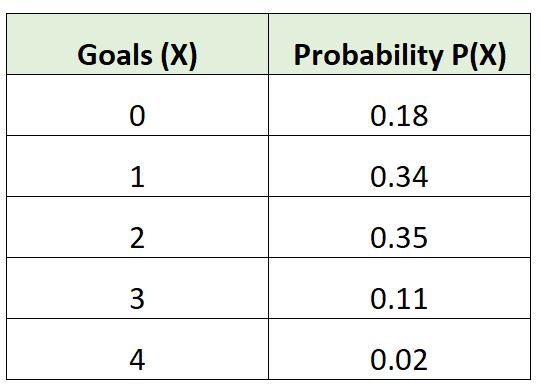
Laten we controleren of deze kansverdeling aan beide vereisten voldoet om geldig te zijn:

1. Elke waarschijnlijkheid moet tussen 0 en 1 liggen.

We kunnen zien dat elke individuele waarschijnlijkheid tussen 0 en 1 ligt.

2. De som van de kansen moet opgeteld 1 zijn.

We kunnen zien dat de som van de kansen optelt tot 1:

Som = 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1

Aan beide voorwaarden is voldaan, dus deze kansverdeling is geldig .

Voorbeeld 2: verkopen in één maand

De volgende kansverdeling toont de waarschijnlijkheid dat een bepaalde verkoper de komende maand een bepaald aantal verkopen zal realiseren:

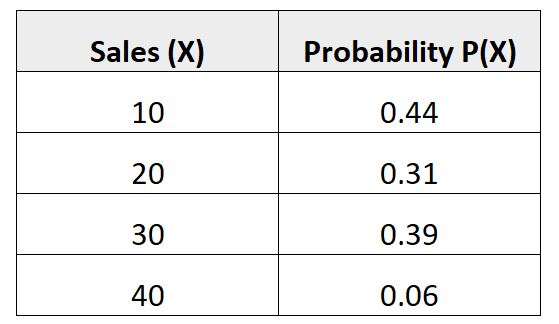
Laten we controleren of deze kansverdeling aan beide vereisten voldoet om geldig te zijn:

1. Elke waarschijnlijkheid moet tussen 0 en 1 liggen.

We kunnen zien dat elke individuele waarschijnlijkheid tussen 0 en 1 ligt.

2. De som van de kansen moet opgeteld 1 zijn.

We zien dat de som van de kansen niet optelt tot 1:

Som = 0,44 + 0,31 + 0,39 + 0,06 = 1,2

Aan beide voorwaarden is niet voldaan en deze kansverdeling is dus ongeldig .

Voorbeeld 3: Aantal batterijstoringen

De volgende kansverdeling vertelt ons de waarschijnlijkheid dat een bepaald voertuig gedurende een periode van 10 jaar een bepaald aantal batterijstoringen zal ervaren:

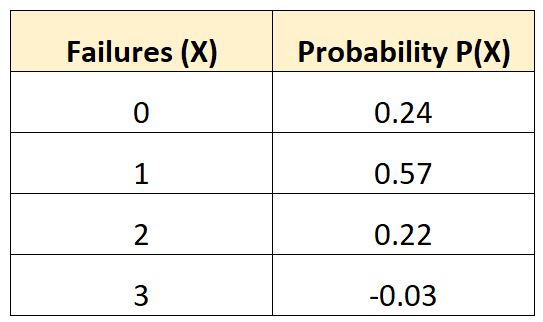
Laten we controleren of deze kansverdeling aan beide vereisten voldoet om geldig te zijn:

1. Elke waarschijnlijkheid moet tussen 0 en 1 liggen.

We kunnen zien dat elke individuele waarschijnlijkheid niet tussen 0 en 1 ligt.

De laatste waarschijnlijkheid in de tabel is een negatieve waarde.

2. De som van de kansen moet opgeteld 1 zijn.

We kunnen zien dat de som van de kansen optelt tot 1:

Som = 0,24 + 0,57 + 0,22 – 0,03 = 1

Aan beide voorwaarden is niet voldaan en deze kansverdeling is dus ongeldig .

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over kansverdelingen:

Hoe het gemiddelde van een kansverdeling te vinden
Hoe de variantie van een kansverdeling te vinden
Hoe de standaarddeviatie van een kansverdeling te vinden